11 Is What Percent Of 25
sandbardeewhy
Nov 21, 2025 · 10 min read
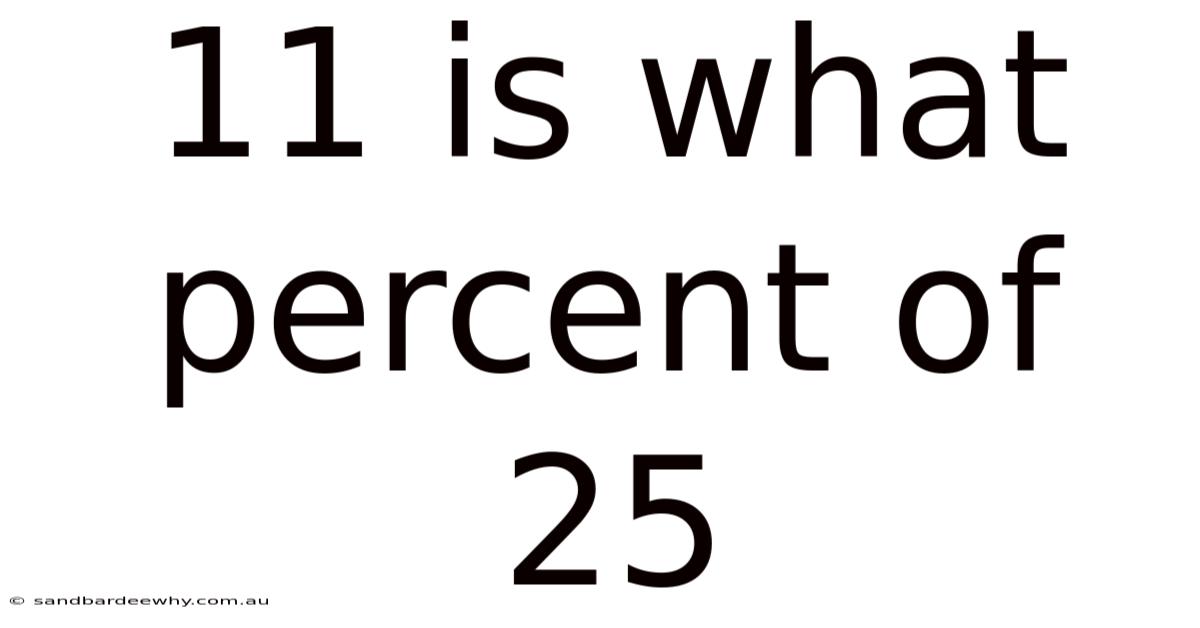
Table of Contents
The aroma of freshly baked cookies fills the air as you help your child with their math homework. They’re stuck on a problem: “11 is what percent of 25?” You remember struggling with percentages yourself, feeling lost in a sea of fractions and decimals. Now, you want to guide your child with confidence, turning a moment of frustration into an opportunity for learning and connection.
Understanding percentages is more than just solving textbook problems; it’s a life skill. From calculating discounts at the store to understanding interest rates on a loan, percentages are woven into the fabric of our daily financial decisions. This article will demystify the process of calculating what percentage one number is of another, using the specific example of "11 is what percent of 25" as our guide. We'll explore the underlying principles, practical applications, and some handy tips to make percentage calculations a breeze.
Main Subheading
Percentages are a fundamental concept in mathematics with widespread applications in everyday life. Whether you're figuring out a sales discount, calculating taxes, or interpreting statistical data, a solid grasp of percentages is essential. At its core, a percentage is simply a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." This "out of one hundred" is what gives percentages their power and versatility, allowing us to easily compare different proportions and ratios.
Understanding how to calculate percentages involves recognizing the relationship between three key components: the base, the part, and the percentage. The base is the whole or the total amount, representing 100%. The part is a portion of that whole, and the percentage expresses the part as a fraction of the base, scaled to a hundred. To solve the problem "11 is what percent of 25," we need to identify these components correctly. In this case, 25 is the base (the whole), 11 is the part (the portion of the whole), and we are trying to find out what percentage 11 represents relative to 25. This article will guide you through the methods to solve this type of problem, providing you with both the formulas and the intuitive understanding needed to confidently tackle any percentage calculation.
Comprehensive Overview
The concept of percentages is deeply rooted in the history of mathematics and commerce. Ancient civilizations, including the Romans, used fractions that were based on 100 to simplify calculations related to taxes, interest rates, and trade. The Romans, for instance, would often compute taxes as a fraction of a property's value, expressing it as a number of centesimae (hundredths). Over time, this practice evolved, and by the Middle Ages, as trade and finance became more sophisticated, the use of percentages became increasingly common throughout Europe.
The modern symbol for percent, "%," evolved gradually over centuries. In the 15th century, mathematicians began using abbreviations such as "per cento" or "P cento" to denote percentages. Eventually, this was shortened to "P. cent," and through various scribal errors and typographical changes, the "P" was replaced by a horizontal line, eventually leading to the "%" symbol we use today. This standardization helped make percentage calculations more accessible and universally understood, further cementing their place in mathematical and financial practices.
To understand how to solve "11 is what percent of 25," let's break down the core principles. The fundamental formula for calculating percentages is:
(Part / Base) * 100 = Percentage
In this formula:
- Part is the portion of the whole that you're interested in.
- Base is the whole or the total amount.
- Percentage is the result you're trying to find, expressed as a percentage.
Applying this to our problem, 11 is the part, and 25 is the base. So, the equation becomes:
(11 / 25) * 100 = Percentage
When you divide 11 by 25, you get 0.44. Multiplying 0.44 by 100 gives you 44. Therefore, 11 is 44% of 25.
Another way to think about this is to convert the fraction 11/25 into an equivalent fraction with a denominator of 100. To do this, you multiply both the numerator and the denominator by 4:
(11 * 4) / (25 * 4) = 44 / 100
This directly shows that 11 is 44 out of 100, or 44%. This method provides a clear visual understanding of what a percentage represents.
Yet another approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up the following proportion:
11 / 25 = x / 100
Here, 'x' represents the percentage we're trying to find. To solve for x, you can cross-multiply:
11 * 100 = 25 * x
1100 = 25x
Then, divide both sides by 25:
x = 1100 / 25
x = 44
This method reinforces the idea that a percentage is a ratio scaled to a base of 100. It's particularly useful for students who are comfortable with solving algebraic equations.
Trends and Latest Developments
In today’s data-driven world, understanding percentages is more critical than ever. We encounter percentages in financial reports, scientific studies, marketing analyses, and countless other contexts. Recent trends highlight the importance of data literacy, which includes a strong foundation in percentage calculations. According to a 2023 study by the Pew Research Center, a significant portion of the adult population struggles with basic numeracy skills, including percentage calculations, which can hinder their ability to make informed decisions about their health, finances, and civic engagement.
Moreover, the increasing prevalence of data visualization tools and dashboards in business and education emphasizes the need for a clear understanding of percentages. These tools often use percentages to represent proportions, growth rates, and comparative data. Without a solid grasp of how percentages work, it can be challenging to accurately interpret these visualizations and draw meaningful conclusions.
Another noteworthy trend is the use of technology to simplify percentage calculations. Numerous online calculators and mobile apps are available that can instantly solve percentage problems. While these tools can be convenient, relying on them exclusively without understanding the underlying principles can lead to a superficial understanding. It's essential to develop a strong foundational understanding of percentages first and then use technology as a tool to enhance efficiency and accuracy.
From a professional standpoint, many industries rely heavily on percentages for analysis and reporting. In finance, percentages are used to calculate returns on investments, interest rates, and profit margins. In marketing, they're used to track conversion rates, customer engagement, and campaign performance. In healthcare, they're used to analyze patient outcomes, track disease prevalence, and assess the effectiveness of treatments. Professionals in these fields need to be able to confidently calculate, interpret, and communicate percentages to make informed decisions and drive strategic initiatives.
In academia, research often involves the use of statistical analysis, which relies heavily on percentages. Researchers use percentages to describe sample demographics, present survey results, and compare different groups. A deep understanding of percentages is crucial for conducting rigorous research and accurately interpreting findings. This ensures that research outcomes are both valid and reliable.
Tips and Expert Advice
When working with percentages, there are several strategies you can employ to ensure accuracy and efficiency. One of the most important tips is to always double-check your work. Percentage calculations can be prone to errors, especially when dealing with complex numbers or multiple steps. Before finalizing your answer, take a moment to review your calculations and ensure that you haven't made any mistakes.
Another useful tip is to estimate your answer before performing the actual calculation. This can help you identify potential errors and ensure that your final answer is reasonable. For example, if you're trying to find what percentage 11 is of 25, you might estimate that it's a little less than 50% since 11 is a little less than half of 25. This mental check can help you catch obvious mistakes and build your intuition for percentage calculations.
Furthermore, practice is key to mastering percentages. The more you work with percentages, the more comfortable and confident you'll become. Try solving a variety of percentage problems, ranging from simple to complex, and gradually increase the difficulty as you improve. You can find practice problems in textbooks, online resources, and even real-world scenarios.
When dealing with word problems involving percentages, it's helpful to break down the problem into smaller, more manageable parts. Identify the key information, such as the base, the part, and the percentage you're trying to find. Then, use the appropriate formula or method to solve for the unknown. Drawing diagrams or creating visual representations can also help you understand the problem and identify the correct approach.
Moreover, understanding the context of the percentage is crucial. Percentages can be easily misinterpreted if you don't understand what they represent. For example, a 10% increase in sales might sound impressive, but if the overall sales volume is very low, the actual increase might be negligible. Always consider the absolute numbers behind the percentages and the context in which they're being used.
Expert advice often includes emphasizing the importance of understanding the underlying concepts rather than just memorizing formulas. While formulas are useful tools, they're not a substitute for a deep understanding of what percentages represent. Focus on developing a conceptual understanding of percentages, and you'll be able to apply them more effectively in a variety of situations. This will also make it easier to remember the formulas and adapt them to different types of problems.
Finally, when presenting percentages, it's important to communicate them clearly and accurately. Use appropriate labels and units, and avoid rounding too much, as this can distort the results. Also, be mindful of the audience you're communicating with and tailor your explanation to their level of understanding. Using visual aids, such as charts and graphs, can also help to communicate percentages more effectively.
FAQ
Q: What is a percentage?
A: A percentage is a way of expressing a number as a fraction of 100. It represents a part of a whole, with the whole being equal to 100%.
Q: How do I calculate what percentage one number is of another?
A: Use the formula: (Part / Base) * 100 = Percentage. Identify the part (the number you're interested in) and the base (the whole or total amount), then plug those values into the formula.
Q: Why are percentages important?
A: Percentages are used in many areas of life, including finance, business, statistics, and everyday decision-making. They help us understand proportions, compare values, and make informed choices.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when there is an increase that exceeds the original amount. For example, if a store increases its prices by 150%, the new price is 2.5 times the original price.
Q: How do I convert a percentage to a decimal?
A: To convert a percentage to a decimal, divide the percentage by 100. For example, 44% is equal to 0.44.
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.44 is equal to 44%.
Conclusion
In summary, understanding how to calculate what percentage one number is of another, such as determining that "11 is what percent of 25," is a valuable skill applicable to various aspects of daily life and professional endeavors. By using the formula (Part / Base) * 100 = Percentage, you can confidently solve percentage problems. In the case of 11 being what percent of 25, the answer is 44%. Mastering percentage calculations not only enhances your mathematical proficiency but also empowers you to make informed decisions in financial, business, and personal contexts.
Now that you have a solid grasp of percentage calculations, put your knowledge to the test. Try solving different percentage problems, explore real-world applications, and share your newfound skills with others. Take a moment to calculate the discounts on your next shopping trip or analyze the growth rate of your favorite company. Your journey to mastering percentages has just begun, and the possibilities are endless. Embrace the challenge and continue to refine your understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
Is Malleable A Physical Or Chemical Property
Nov 21, 2025
-
How Many Cups Is 300 Grams Of Sugar
Nov 21, 2025
-
How Much Nickels Make 2 Dollars
Nov 21, 2025
-
How Many Quarts In 5 Gallon Bucket
Nov 21, 2025
-
How Much Is One Gallon In Oz
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 11 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.