12 Is 30 Percent Of What Number
sandbardeewhy
Nov 27, 2025 · 12 min read
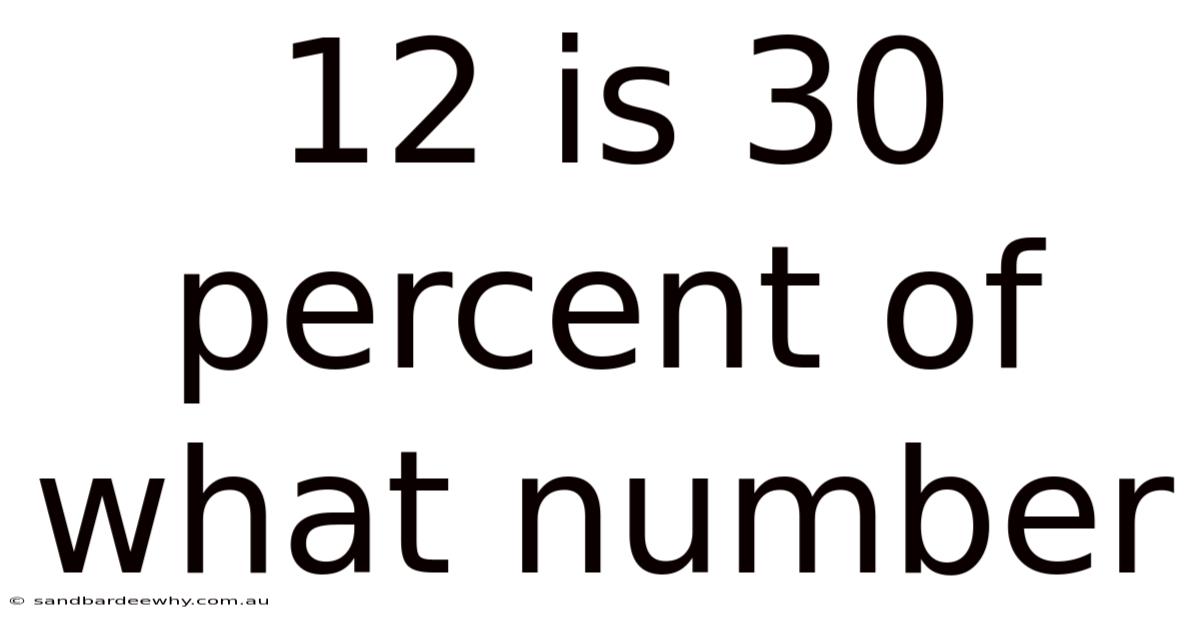
Table of Contents
Have you ever been in a situation where you knew a part of a total and the percentage it represents, but you needed to find out the total? This happens more often than we realize. Whether you're calculating discounts, figuring out proportions in recipes, or even understanding statistics, knowing how to solve this type of problem is incredibly useful. It’s not just about the math; it’s about understanding the relationships between numbers and how they apply to real-life situations.
Imagine you're at a store, and a sign says that an item you want is 30% off, and the discount amounts to $12. You might wonder, "What was the original price of this item?" Or perhaps you are managing a project and realize that the $12 you've spent so far represents 30% of your total budget. Quickly calculating the full budget can help you stay on track. The ability to solve "12 is 30 percent of what number?" is a surprisingly practical skill that empowers you to make informed decisions every day. Let's dive into how to solve this and similar problems with confidence.
Unveiling the Mystery: 12 is 30 Percent of What Number?
The question "12 is 30 percent of what number?" is a classic percentage problem that can be easily solved using basic algebraic principles. Understanding how to tackle this question is fundamental to grasping percentages and their applications in everyday life. This seemingly simple question opens the door to a broader understanding of proportions, ratios, and mathematical problem-solving techniques.
At its core, this problem is about finding the whole when you know a part and the percentage that part represents. To solve it, we need to translate the words into a mathematical equation and then isolate the unknown variable. There are several methods to approach this, from using proportions to converting percentages into decimals. Each method provides a slightly different lens through which to view the problem, but they all lead to the same solution. Knowing how to solve this type of problem not only strengthens your math skills but also enhances your ability to analyze and interpret numerical information in various contexts.
Comprehensive Overview: The Foundations of Percentage Problems
To truly understand how to solve "12 is 30 percent of what number?", it's essential to delve into the underlying concepts of percentages, proportions, and their mathematical representation. This section will explore the definitions, historical context, and the step-by-step methods to tackle this type of problem effectively.
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Percentages are used to express how large one quantity is relative to another quantity. For example, if you score 80 out of 100 on a test, you scored 80 percent (80%) of the total possible points. Percentages are ubiquitous in daily life, from calculating discounts to understanding interest rates.
The concept of percentages has ancient roots, dating back to the Roman Empire. The Romans used fractions that were multiples of 1/100 to calculate taxes and trade transactions. However, the modern percentage symbol (%) and its widespread use didn't become common until the 15th century. The rise of commerce and banking during the Renaissance spurred the need for a standardized way to express proportions and ratios, leading to the widespread adoption of percentages.
The problem "12 is 30 percent of what number?" can be approached using several methods, but the most common involve converting the percentage into a decimal or setting up a proportion. Here's a breakdown of each method:
-
Decimal Conversion Method:
- Convert the percentage to a decimal by dividing it by 100. In this case, 30% becomes 30/100 = 0.30.
- Set up an equation where the known part (12) is equal to the decimal multiplied by the unknown whole (x):
12 = 0.30 * x - Solve for x by dividing both sides of the equation by 0.30:
x = 12 / 0.30 x = 40
Therefore, 12 is 30 percent of 40.
-
Proportion Method:
- Set up a proportion where the known part (12) is to the unknown whole (x) as the percentage (30) is to 100:
12 / x = 30 / 100 - Cross-multiply to solve for x:
12 * 100 = 30 * x 1200 = 30x - Divide both sides by 30 to isolate x:
x = 1200 / 30 x = 40
Again, we find that 12 is 30 percent of 40.
- Set up a proportion where the known part (12) is to the unknown whole (x) as the percentage (30) is to 100:
Both methods are mathematically sound and provide the same answer. The choice between them often comes down to personal preference or the specific context of the problem. Understanding both methods allows for greater flexibility and a deeper understanding of percentage calculations.
In addition to these direct calculation methods, it's crucial to understand the underlying principle of proportionality. Percentages are essentially ratios, and understanding how to manipulate ratios can simplify many mathematical problems. For instance, recognizing that 30% is equivalent to the fraction 3/10 can sometimes provide a quicker path to the solution.
For example, if 12 is 3/10 of a number, you can find 1/10 of the number by dividing 12 by 3, which equals 4. Then, multiply 4 by 10 to find the whole number, which is 40. This approach highlights the relationship between fractions, percentages, and proportions.
Trends and Latest Developments in Percentage Calculations
While the fundamental principles of percentage calculations remain constant, the ways in which they are applied and taught have evolved with technological and educational advancements. Today, there's a greater emphasis on practical applications and conceptual understanding rather than rote memorization.
One significant trend is the integration of technology into learning percentage calculations. Online calculators, educational apps, and interactive simulations make it easier for students to visualize and manipulate percentages. These tools often provide step-by-step solutions and immediate feedback, helping learners identify and correct their mistakes more efficiently.
Another trend is the increasing focus on financial literacy. Schools and educational programs are incorporating percentage calculations into lessons on budgeting, investing, and understanding financial statements. This prepares students to make informed financial decisions in their personal and professional lives.
Data analysis and statistics have also driven the need for a deeper understanding of percentages. Professionals in various fields, from marketing to healthcare, rely on percentages to interpret data, identify trends, and make strategic decisions. As a result, there's a growing demand for individuals who can not only calculate percentages but also understand their statistical significance and implications.
Educators are also exploring innovative teaching methods to make percentage calculations more engaging and relevant. Real-world examples, case studies, and project-based learning are used to illustrate the practical applications of percentages. For instance, students might analyze sales data to calculate profit margins or track the growth of social media followers as a percentage of total users.
Tips and Expert Advice for Mastering Percentage Problems
Mastering percentage problems, such as "12 is 30 percent of what number?", requires a combination of understanding the basic principles and practicing problem-solving techniques. Here are some expert tips and advice to help you improve your skills:
-
Understand the Language:
- Pay close attention to the wording of the problem. Key phrases like "percent of," "is what percent of," and "what is x percent of" have different meanings and require different approaches.
- Translate the words into a mathematical equation carefully. For example, "12 is 30 percent of what number?" translates to 12 = 0.30 * x.
-
Master the Conversion:
- Be proficient in converting percentages to decimals and fractions, and vice versa. This is a fundamental skill for solving percentage problems efficiently.
- Remember that to convert a percentage to a decimal, divide by 100. To convert a decimal to a percentage, multiply by 100.
-
Use Proportions Wisely:
- Set up proportions correctly. Ensure that the corresponding values are in the same positions in the proportion.
- Cross-multiplication can simplify the process of solving proportions, but make sure you understand why it works mathematically.
-
Estimate and Check Your Answers:
- Before solving a problem, estimate the answer to get a sense of what the correct solution should be. This can help you identify errors in your calculations.
- After solving a problem, check your answer by plugging it back into the original equation to see if it makes sense. For example, if you find that 12 is 30 percent of 40, verify that 0.30 * 40 = 12.
-
Practice Regularly:
- The key to mastering percentage problems is practice. Work through a variety of problems to build your confidence and skills.
- Use online resources, textbooks, and worksheets to find practice problems.
-
Visualize Percentages:
- Use visual aids, such as pie charts and bar graphs, to understand percentages better. Visualizing percentages can help you grasp the concept of proportion and relative size.
- Think of percentages as parts of a whole. For example, 30% is like having 30 slices of a pizza that has 100 slices in total.
-
Break Down Complex Problems:
- Complex percentage problems can be broken down into smaller, more manageable steps. Identify the key information and the relationships between the values.
- Use intermediate calculations to simplify the problem. For example, if you need to find a percentage increase followed by a percentage decrease, calculate each step separately.
-
Apply Real-World Examples:
- Relate percentage problems to real-world situations. This can make the problems more engaging and easier to understand.
- Think about how percentages are used in everyday life, such as calculating discounts, interest rates, and taxes.
-
Understand Percentage Change:
- Learn how to calculate percentage increase and decrease. This involves finding the difference between the new value and the original value, and then dividing by the original value.
- Be careful to use the correct base when calculating percentage change. The base is the value from which the change is calculated.
-
Seek Help When Needed:
- Don't hesitate to ask for help if you're struggling with percentage problems. Consult with a teacher, tutor, or online forum.
- Explain your thought process to others to identify any gaps in your understanding.
FAQ: Addressing Common Questions About Percentage Problems
Q: What is the formula for finding the percentage of a number?
A: To find what percentage a number (A) is of another number (B), use the formula: (A / B) * 100. For example, to find what percentage 12 is of 40, calculate (12 / 40) * 100 = 30%.
Q: How do I convert a percentage to a decimal?
A: To convert a percentage to a decimal, divide the percentage by 100. For example, 30% becomes 30 / 100 = 0.30.
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.30 becomes 0.30 * 100 = 30%.
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase is the relative increase in a value, calculated as [(New Value - Original Value) / Original Value] * 100. Percentage decrease is the relative decrease in a value, calculated as [(Original Value - New Value) / Original Value] * 100.
Q: How do I solve for the original price after a discount?
A: If you know the discounted price and the percentage discount, you can find the original price by dividing the discounted price by (1 - discount percentage as a decimal). For example, if an item is $70 after a 30% discount, the original price is $70 / (1 - 0.30) = $70 / 0.70 = $100.
Q: Can percentages be greater than 100%?
A: Yes, percentages can be greater than 100%. This typically occurs when describing an increase or growth relative to an original value. For example, if a company's revenue doubles, it has experienced a 100% increase, and if it triples, it has experienced a 200% increase.
Q: How are percentages used in statistics?
A: Percentages are used in statistics to express relative frequencies and proportions. They are used to summarize data, compare groups, and identify trends. For example, percentages can be used to show the proportion of people who support a particular political candidate or the percentage of students who pass a standardized test.
Q: What is a percentage point?
A: A percentage point is the unit for the arithmetic difference of two percentages. For example, if a support level increases from 30% to 40%, that is an increase of 10 percentage points. It is important to distinguish this from a 10% increase, which would mean the support level increased by 10% of 30% (or 3 percentage points) to 33%.
Q: How do I calculate compound interest?
A: Compound interest is calculated using the formula: A = P (1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the annual interest rate (as a decimal), n is the number of times that interest is compounded per year, and t is the number of years the money is invested or borrowed for.
Q: Where can I find more resources for learning about percentages?
A: There are many online resources, textbooks, and educational websites that offer lessons and practice problems on percentages. Some popular resources include Khan Academy, Mathway, and Purplemath.
Conclusion: Mastering Percentages for Everyday Success
Understanding how to solve percentage problems, like answering the question "12 is 30 percent of what number?", is a valuable skill that extends far beyond the classroom. From managing personal finances to making informed decisions in business, percentages are an integral part of our daily lives.
By mastering the basic principles, practicing problem-solving techniques, and applying real-world examples, you can develop a strong foundation in percentage calculations. Whether you choose to use decimal conversion, proportions, or visual aids, the key is to understand the underlying concepts and apply them consistently.
Continue to practice and explore the various applications of percentages in different contexts. Challenge yourself with more complex problems and seek out opportunities to apply your skills in real-world situations. As you become more confident and proficient in percentage calculations, you'll find that they empower you to make better decisions, analyze information more effectively, and navigate the complexities of modern life with greater ease.
Now that you've deepened your understanding of percentages, take the next step by exploring related mathematical concepts, such as ratios, proportions, and statistics. Consider enrolling in a course or workshop to further enhance your skills and knowledge. Share your newfound expertise with others and help them unlock the power of percentages in their own lives.
Latest Posts
Latest Posts
-
How Tall Is 5 2 In Meters
Nov 27, 2025
-
How Many Dry Quarts In A Gallon
Nov 27, 2025
-
What Is 3 Qt Of Water
Nov 27, 2025
-
What Is A Credibility Statement In A Speech
Nov 27, 2025
-
How Many 8 Ounce Cups In A Gallon
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about 12 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.