13 Out Of 20 As A Percentage
sandbardeewhy
Nov 28, 2025 · 12 min read
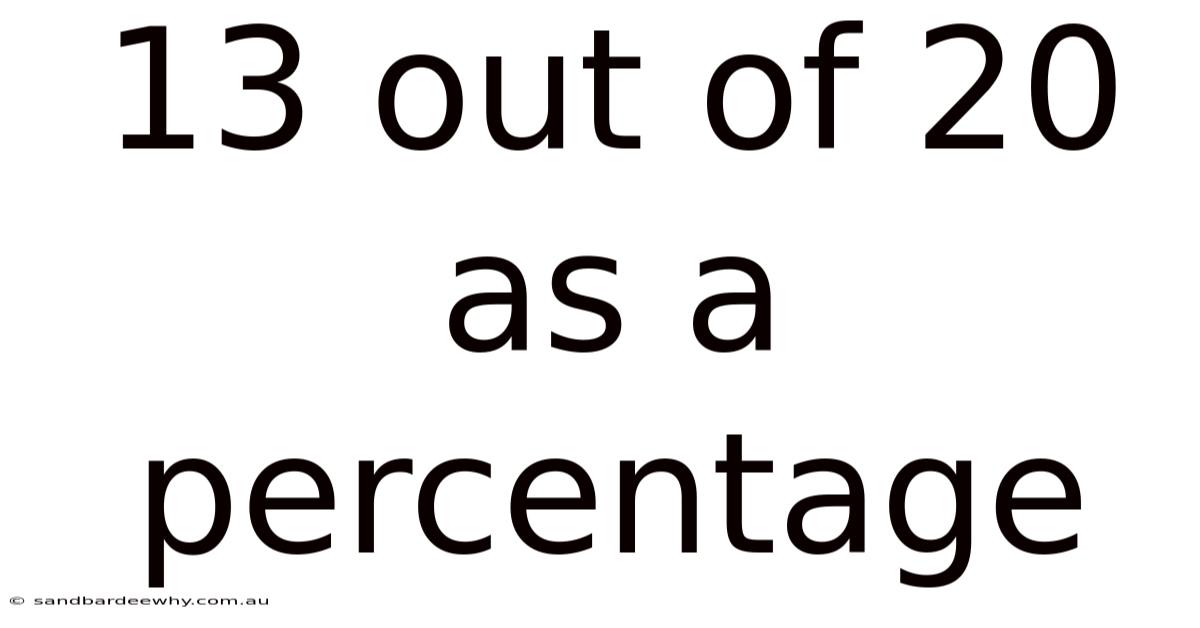
Table of Contents
Imagine you're at a school fair, trying your luck at a ring toss game. There are twenty bottles, and you manage to ring thirteen of them. The announcer asks, "So, what's your percentage, champ?" Suddenly, everyone's looking at you, expecting a quick calculation. It's a moment where understanding how to convert a fraction like 13 out of 20 into a percentage becomes incredibly useful.
Or perhaps you're reviewing the results of a recent customer satisfaction survey. Out of 20 responses, 13 indicate high satisfaction. To present this data effectively to your team, you want to express it as a percentage. This simple conversion can transform raw numbers into a relatable and easily understandable metric, revealing how well your company is meeting customer expectations. So, how do you go from 13 out of 20 to a percentage? Let's dive in.
Understanding the Basics: Converting Fractions to Percentages
To understand how to express 13 out of 20 as a percentage, we first need to grasp the fundamental concept of what a percentage represents. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, a percentage is simply a way of expressing a number as a fraction of 100. Converting a fraction to a percentage involves expressing the fraction with a denominator of 100.
The mathematical foundation behind this conversion is quite straightforward. A fraction represents a part of a whole. In our case, 13 out of 20 represents 13 parts of a whole that is divided into 20 equal parts. To convert this to a percentage, we need to find an equivalent fraction where the denominator is 100. This allows us to directly read off the numerator as the percentage.
Historically, the concept of percentages has been used for centuries in various forms. Ancient civilizations used proportional parts to calculate taxes, interest, and measurements. However, the modern concept of percentage, as we know it, gained prominence during the Renaissance with the growth of commerce and the need for standardized financial calculations. Merchants, bankers, and scholars needed a consistent way to express ratios and proportions, leading to the widespread adoption of percentages.
The notation "%" is believed to have evolved from the Italian abbreviation "cento" (meaning hundred), which was often written as "c." Over time, this was further abbreviated and eventually transformed into the symbol we use today. This evolution reflects the increasing importance of percentages in everyday calculations, from finance and statistics to everyday shopping discounts.
Why is it so important to convert fractions to percentages? Percentages provide a standardized way to compare different fractions, making it easier to understand proportions and ratios. For instance, comparing 13/20 to 40/50 directly might not be immediately intuitive. However, converting both to percentages (65% and 80%, respectively) makes the comparison much clearer. This standardization is particularly useful in fields like finance, statistics, and economics, where large datasets and complex comparisons are common.
Comprehensive Overview: Calculating 13 out of 20 as a Percentage
The process of converting 13 out of 20 as a percentage involves a simple calculation that can be broken down into a few steps. The most common and straightforward method is to divide the numerator (13) by the denominator (20) and then multiply the result by 100. This method directly converts the fraction into a percentage.
Here’s the calculation:
- Divide 13 by 20: 13 ÷ 20 = 0.65
- Multiply the result by 100: 0.65 × 100 = 65
Therefore, 13 out of 20 as a percentage is 65%. This means that 13 is 65% of 20. Understanding this simple calculation can be incredibly useful in various scenarios, from academic settings to everyday problem-solving.
Another way to approach this calculation is by finding an equivalent fraction with a denominator of 100. To do this, you need to determine what number you can multiply the original denominator (20) by to get 100. In this case, 20 multiplied by 5 equals 100. Then, you multiply both the numerator and the denominator by this number.
Here's how it works:
- Determine the multiplier: 100 ÷ 20 = 5
- Multiply both the numerator and the denominator by 5:
- Numerator: 13 × 5 = 65
- Denominator: 20 × 5 = 100
This gives you the fraction 65/100, which directly translates to 65%. This method is particularly useful for understanding the proportional relationship and visualizing the fraction as a part of a whole of 100.
Why do these methods work? Both methods are based on the fundamental principle of proportional relationships. When you divide 13 by 20, you are finding the decimal equivalent of the fraction. Multiplying this decimal by 100 scales it to represent the number out of 100, which is the definition of a percentage. Similarly, finding an equivalent fraction with a denominator of 100 directly expresses the proportion as a percentage.
Understanding these calculations is not just about getting the right answer; it’s about understanding the underlying mathematical principles. This understanding allows you to apply the same logic to a variety of problems, whether you're calculating discounts, analyzing statistics, or managing budgets.
Trends and Latest Developments in Percentage Usage
Percentages are ubiquitous in modern data presentation and analysis, but how they are used and interpreted is constantly evolving. Recent trends highlight the importance of contextual understanding and the potential for misinterpretation. It's not enough to simply calculate a percentage; understanding the underlying data and potential biases is crucial.
One significant trend is the increasing use of interactive data visualizations. Instead of presenting raw percentages, data analysts are using tools that allow users to explore the data, see the sample sizes, and understand the margin of error. This interactivity helps prevent misinterpretations and allows for a more nuanced understanding of the data. For example, a pie chart might show that 65% of customers prefer a certain product, but an interactive chart could also show that this is based on a small sample size, making the result less conclusive.
Another trend is the growing awareness of statistical significance. Just because a percentage is different doesn't mean it's meaningful. Statisticians emphasize the importance of hypothesis testing and p-values to determine whether an observed difference is likely due to chance or a real effect. This is particularly important in fields like medicine and social sciences, where decisions are based on statistical data.
Professional insights also reveal that how percentages are framed can significantly impact perception. For example, presenting a medical treatment as having a "90% success rate" sounds much more appealing than saying it has a "10% failure rate," even though they convey the same information. This framing effect is a key consideration in marketing, public health, and policy-making. Understanding how to present percentages in a way that is both accurate and persuasive is a valuable skill.
Moreover, the use of percentages in financial reporting is becoming more standardized. Regulatory bodies are pushing for greater transparency and consistency in how companies report financial data, including percentages. This standardization aims to make it easier for investors and stakeholders to compare the performance of different companies and make informed decisions.
The rise of big data and data analytics has also influenced how percentages are used. With access to vast amounts of data, analysts can calculate percentages across various segments and dimensions, providing deeper insights into complex phenomena. This requires sophisticated tools and techniques to ensure the accuracy and reliability of the results.
Tips and Expert Advice on Using Percentages Effectively
Using percentages effectively involves more than just knowing how to calculate them. It's about understanding their context, potential pitfalls, and how to communicate them clearly. Here are some practical tips and expert advice to help you use percentages more effectively in various situations.
1. Provide Context: Always provide context when presenting percentages. A percentage without context is often meaningless or misleading. For example, saying "sales increased by 50%" sounds impressive, but it's essential to know the starting point. If sales were initially very low, a 50% increase might still result in a modest overall sales figure. Similarly, when presenting 13 out of 20 as a percentage, make sure to specify what "20" represents. Is it the total number of customers surveyed, the total number of products sold, or something else? Providing this context ensures that your audience understands the significance of the percentage.
2. Understand the Base: Be aware of the base number from which the percentage is calculated. A small change in the base can lead to significant changes in the percentage. For instance, if a company's profit margin increases from 2% to 4%, it's a 100% increase. However, the actual increase in profit margin is only 2 percentage points. This distinction is crucial in financial analysis. Always consider the absolute values alongside the percentages to get a complete picture.
3. Avoid Misleading Comparisons: Be cautious when comparing percentages from different datasets or populations. Make sure that the datasets are comparable and that any differences are not due to confounding factors. For example, comparing the percentage of satisfied customers in two different surveys is only valid if the surveys used the same methodology and targeted similar customer groups.
4. Use Visual Aids: Use visual aids such as charts and graphs to present percentages in a clear and engaging way. Visualizations can help your audience quickly grasp the key insights and trends. Pie charts are useful for showing the distribution of categories, while bar graphs are effective for comparing percentages across different groups. Line graphs can illustrate changes in percentages over time.
5. Be Clear and Concise: Use clear and concise language when communicating percentages. Avoid jargon and technical terms that your audience may not understand. Round percentages to a reasonable number of decimal places to avoid overwhelming your audience with unnecessary detail. For example, instead of saying "65.384615%," round it to "65.4%" or even "65%" if the level of precision is not critical.
6. Highlight Significant Changes: Focus on highlighting significant changes or trends in the data. Don't just present a list of percentages; explain what they mean and why they are important. For example, if you notice a significant increase or decrease in a particular percentage, investigate the underlying causes and explain them to your audience.
7. Consider Sample Size: Always consider the sample size when interpreting percentages. Percentages based on small sample sizes are less reliable and may not be representative of the population. If the sample size is small, acknowledge this limitation and avoid making strong generalizations based on the results.
FAQ: Frequently Asked Questions About Percentages
Q: What is the difference between a percentage and a percentage point?
A: A percentage is a ratio expressed as a fraction of 100, while a percentage point is the simple difference between two percentages. For example, if a company's profit margin increases from 5% to 7%, it's an increase of 2 percentage points. The percentage increase, however, is (2/5) * 100 = 40%.
Q: How do I calculate the percentage increase or decrease?
A: To calculate the percentage increase or decrease, use the following formula: ((New Value - Old Value) / Old Value) * 100. If the result is positive, it's a percentage increase; if it's negative, it's a percentage decrease.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a value to a base that is smaller than the value itself. For example, if a company's revenue doubles, it's a 100% increase, and if it triples, it's a 200% increase.
Q: How do I convert a percentage back to a fraction or decimal?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the fraction if possible. For example, 65% = 65/100 = 13/20. To convert a percentage to a decimal, divide the percentage by 100. For example, 65% = 0.65.
Q: Why are percentages used so frequently in statistics?
A: Percentages are used frequently in statistics because they provide a standardized way to compare different datasets and populations. They make it easier to understand proportions and ratios, and they allow for meaningful comparisons even when the underlying numbers are very different.
Q: How do I avoid common mistakes when working with percentages?
A: To avoid common mistakes, always double-check your calculations, provide context when presenting percentages, be aware of the base number, and avoid misleading comparisons. Also, be cautious when working with small sample sizes and always consider the potential for bias.
Q: Is there a quick way to calculate percentages without a calculator?
A: Yes, there are several mental math techniques for calculating percentages. For example, to find 10% of a number, simply move the decimal point one place to the left. To find 50% of a number, divide it by 2. To find 25% of a number, divide it by 4. You can combine these techniques to calculate other percentages as well.
Conclusion
Understanding how to calculate and interpret percentages is a fundamental skill that is applicable in numerous aspects of life. Converting 13 out of 20 as a percentage is a straightforward calculation that yields 65%, but the real value lies in understanding the context and implications of that percentage. Whether you're analyzing survey results, calculating discounts, or interpreting financial data, knowing how to use percentages effectively can help you make informed decisions and communicate your ideas clearly.
By providing context, understanding the base, avoiding misleading comparisons, and using visual aids, you can ensure that your use of percentages is both accurate and meaningful. Remember to consider the sample size and be aware of potential biases to avoid misinterpretations.
Now that you understand the ins and outs of converting fractions to percentages, take the next step and apply this knowledge to real-world scenarios. Practice calculating percentages in different contexts and explore how they can be used to gain insights and make better decisions. Share your newfound knowledge with others and help them understand the power and importance of percentages in everyday life. Start by calculating the percentages in your daily expenses or analyzing the results of a recent survey. The possibilities are endless, and the more you practice, the more confident you'll become in your ability to use percentages effectively.
Latest Posts
Latest Posts
-
What Is A Secondary Consumer In A Food Chain
Nov 28, 2025
-
How To Find Height Of Rectangular Prism
Nov 28, 2025
-
What Is The Definition Of Limited Government
Nov 28, 2025
-
What Is The Overall Purpose Of Photosynthesis
Nov 28, 2025
-
What Is The Reciprocal Of 2
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about 13 Out Of 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.