148 Out Of 1000 As A Percentage
sandbardeewhy
Nov 22, 2025 · 10 min read
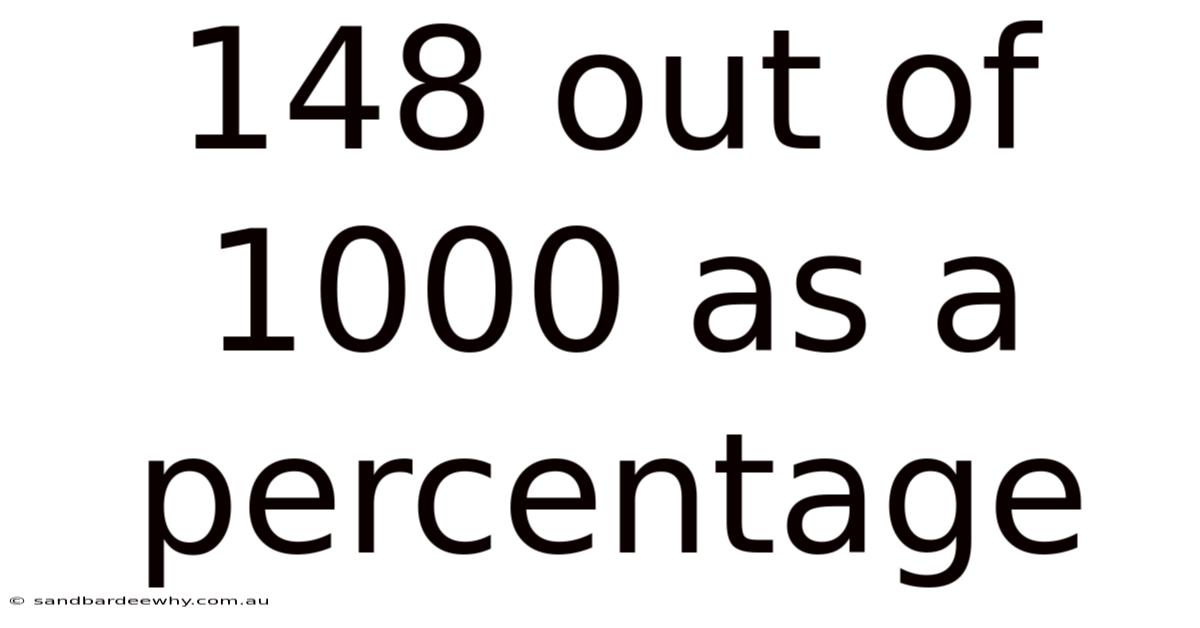
Table of Contents
Imagine you're at a bustling farmers market, overflowing with colorful produce. The aroma of freshly baked bread fills the air, and vendors proudly display their goods. You spot a stall selling the most vibrant, ruby-red strawberries you've ever seen. The sign reads, "148 out of 1000 strawberries are organically grown!" Your curiosity piqued, you wonder, "What percentage of these strawberries are actually organic?"
Or perhaps you are an educator reviewing student performance. You note that 148 out of 1000 students in a school actively participate in extracurricular activities. While the raw number gives you some insight, you need a more intuitive understanding – a percentage – to easily compare this figure to other schools or previous years. Converting "148 out of 1000" into a percentage provides that clearer picture, allowing for quick comparisons and better decision-making. In this article, we'll explore how to convert the fraction "148 out of 1000" into a percentage, offering not just the calculation but also the underlying concepts and practical applications.
Understanding the Basics of Percentages
At its core, a percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Understanding percentages is fundamental in various aspects of life, from calculating discounts while shopping to interpreting statistical data in research papers. Percentages offer a standardized way to compare proportions, making complex information more accessible and understandable.
Percentages simplify complex ratios and proportions. Instead of grappling with fractions or decimals, a percentage provides an immediate sense of scale. For example, saying that 50% of students passed an exam is far more intuitive than saying that 0.5 of the students passed. The concept is universally applicable, transcending cultural and linguistic barriers, making it a powerful tool for communication and analysis. Whether you're dealing with financial data, scientific research, or everyday scenarios, percentages help you make sense of the numbers and draw meaningful conclusions.
The Foundation: Ratios and Fractions
Before diving into percentages, it's essential to understand ratios and fractions. A ratio compares two quantities, indicating how much of one thing there is compared to another. It can be written in several ways, such as "a to b," "a:b," or as a fraction "a/b." The fraction "a/b" represents a parts out of a total of b parts.
In our specific case, "148 out of 1000" is a ratio that can be written as the fraction 148/1000. This fraction represents the proportion of a specific subset (148) within a larger set (1000). Understanding this foundation is crucial because a percentage is simply a special type of fraction where the denominator is always 100. Converting a fraction to a percentage involves scaling the fraction so that the denominator becomes 100, thereby expressing the original ratio in terms of "out of 100."
From Fraction to Percentage: The Conversion Process
The process of converting a fraction to a percentage is straightforward. The core idea is to express the fraction as an equivalent fraction with a denominator of 100. This is typically achieved through multiplication or division.
The general formula for converting a fraction to a percentage is:
Percentage = (Fraction) x 100
Applying this to our example, where the fraction is 148/1000, we get:
Percentage = (148/1000) x 100
To solve this, you first divide 148 by 1000, which equals 0.148. Then, you multiply 0.148 by 100.
Percentage = 0.148 x 100 = 14.8%
Therefore, 148 out of 1000 expressed as a percentage is 14.8%. This means that for every 1000 items, 148 of them represent a specific characteristic or condition, which corresponds to 14.8 for every 100 items.
Real-World Examples of Percentage Calculations
Percentages are ubiquitous in everyday life. Understanding how to calculate and interpret them can significantly enhance decision-making and comprehension in various scenarios. Here are some common real-world examples where percentage calculations are invaluable:
-
Retail Discounts: When shopping, discounts are often expressed as percentages. For instance, a "20% off" sale means that the price of an item is reduced by 20% of its original value. To calculate the final price, you determine 20% of the original price and subtract it from the original price.
-
Financial Investments: In finance, percentages are used to express interest rates, investment returns, and portfolio allocations. For example, an investment that yields a "5% annual return" will increase in value by 5% each year.
-
Academic Grading: Teachers and professors often use percentages to represent student performance. A student who scores 85 out of 100 on a test receives a grade of 85%. These percentages are then used to calculate overall course grades.
-
Statistical Analysis: Researchers use percentages to summarize and interpret data. For instance, a study might report that "60% of participants experienced a positive outcome." These percentages help convey the significance and implications of the research findings.
-
Health and Nutrition: Percentages are used to represent nutritional information on food labels, such as "Percent Daily Value." These values indicate the proportion of recommended daily intake that a serving of food provides.
Trends and Latest Developments
The use of percentages in data representation is continuously evolving with the advent of new technologies and analytical methods. Modern data visualization tools and software platforms rely heavily on percentages to present complex datasets in an accessible format. This trend is driven by the increasing need for data literacy across various industries and the desire to communicate information effectively to diverse audiences.
Enhanced Data Visualization
Today’s data visualization tools offer interactive dashboards that allow users to explore data through percentages and other metrics. These tools enable real-time analysis and reporting, making it easier to identify trends, patterns, and anomalies. For example, businesses use these tools to track sales performance, customer engagement, and market trends, often represented as percentages for quick understanding.
Machine Learning and Predictive Analysis
Machine learning algorithms often use percentages to express the confidence level of predictions. For instance, a model might predict that a customer has an 80% chance of purchasing a product. This probabilistic approach is invaluable in decision-making processes, helping businesses allocate resources and prioritize actions based on the likelihood of success.
Integration with Artificial Intelligence
Artificial intelligence (AI) is further enhancing the use of percentages by automating the analysis and interpretation of data. AI-powered systems can identify significant percentage changes, flag potential risks, and recommend optimal strategies. This integration streamlines data analysis workflows, allowing professionals to focus on strategic initiatives rather than manual calculations.
Expert Insights on Percentage Usage
Experts emphasize the importance of context when interpreting percentages. While a percentage can provide a clear snapshot of a proportion, it’s crucial to consider the underlying sample size and the potential for bias. A small sample size can lead to skewed percentages that do not accurately reflect the broader population. Similarly, biased data can result in misleading percentages that distort the true picture.
Additionally, experts advise caution when comparing percentages across different groups or time periods. Factors such as changes in methodology, data collection techniques, or population characteristics can affect the validity of comparisons. Therefore, it’s essential to carefully evaluate the data sources and methodologies before drawing conclusions based on percentage comparisons.
Tips and Expert Advice
Calculating percentages accurately and efficiently is a valuable skill in many contexts. Here are some practical tips and expert advice to help you master percentage calculations:
Master the Basic Formula
The foundation of percentage calculations is the formula: Percentage = (Part / Whole) x 100. Understanding this formula and how to apply it is crucial for solving a wide range of percentage-related problems. Always identify the "part" (the subset you're interested in) and the "whole" (the total set) before plugging the numbers into the formula.
For example, if you want to find what percentage 30 is of 200, 30 is the "part" and 200 is the "whole." Applying the formula:
Percentage = (30 / 200) x 100 = 0.15 x 100 = 15%
Use Mental Math Techniques
Developing mental math skills can significantly speed up percentage calculations. Here are some useful techniques:
- Finding 10%: To find 10% of a number, simply move the decimal point one place to the left. For example, 10% of 350 is 35.
- Finding 1%: To find 1% of a number, move the decimal point two places to the left. For example, 1% of 350 is 3.5.
- Breaking Down Percentages: Break down complex percentages into simpler parts. For instance, to find 15% of a number, calculate 10% and 5% separately and then add them together. If you want to calculate 15% of 350, you can find 10% (35) and 5% (half of 10%, which is 17.5), and then add them together: 35 + 17.5 = 52.5.
Leverage Technology
In today's digital age, numerous tools and apps can assist with percentage calculations. Calculators, spreadsheet software, and online percentage calculators are readily available to streamline the process. These tools not only ensure accuracy but also save time, especially when dealing with complex calculations or large datasets.
Spreadsheet software like Microsoft Excel and Google Sheets have built-in functions for percentage calculations. You can use formulas like "=A1/B1" to calculate the fraction and then format the cell as a percentage to display the result. Online percentage calculators are also convenient for quick calculations on the go.
Practice with Real-World Scenarios
The best way to improve your percentage calculation skills is to practice with real-world scenarios. Look for opportunities to apply percentages in your daily life, such as calculating discounts while shopping, determining tips at restaurants, or analyzing financial data. The more you practice, the more confident and proficient you'll become.
For example, when you're at a store and see a sale offering "30% off," try to calculate the discounted price in your head before looking at the tag. This exercise will not only improve your mental math skills but also help you make informed purchasing decisions.
FAQ
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, the decimal 0.75 becomes 75% (0.75 x 100 = 75).
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase measures how much a quantity has grown relative to its original value, while percentage decrease measures how much a quantity has shrunk relative to its original value. The formulas are:
- Percentage Increase = [(New Value - Original Value) / Original Value] x 100
- Percentage Decrease = [(Original Value - New Value) / Original Value] x 100
Q: How do I calculate a percentage of a given number?
A: To calculate a percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, to find 20% of 150, multiply 150 by 0.20 (20% expressed as a decimal): 150 x 0.20 = 30.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when measuring an increase relative to an original value. For example, if a company's revenue doubles, the percentage increase is 100%. If it triples, the percentage increase is 200%.
Q: How do I calculate the original value if I know the percentage and the result?
A: To calculate the original value, divide the result by the percentage (expressed as a decimal). For example, if 25% of a number is 50, the original number is 50 / 0.25 = 200.
Conclusion
Understanding how to express "148 out of 1000" as a percentage—which we've determined to be 14.8%—is more than just a mathematical exercise. It's a practical skill with applications in everyday life, from understanding discounts to interpreting statistical data. By mastering the fundamental concepts of ratios, fractions, and percentages, you can confidently analyze and interpret information presented in percentage form.
Take the time to practice these calculations and apply them to real-world scenarios. Whether you're analyzing financial reports, comparing shopping deals, or understanding statistical data, the ability to work with percentages will empower you to make informed decisions and gain a deeper understanding of the world around you. Share this knowledge with friends, family, or colleagues, and encourage them to explore the power of percentages in their own lives. What other number sets would you like to see converted into percentages?
Latest Posts
Latest Posts
-
When Did The Yazoo Land Act Happen
Nov 22, 2025
-
What Is 45 Cm In Inches
Nov 22, 2025
-
What Does A Poison Tree Tattoo Mean
Nov 22, 2025
-
How Many Credits To Graduate High School In Fl
Nov 22, 2025
-
Does Cu2 Ion Reacts With Glycerol
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about 148 Out Of 1000 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.