15 Is 6 Percent Of What Number
sandbardeewhy
Nov 27, 2025 · 9 min read
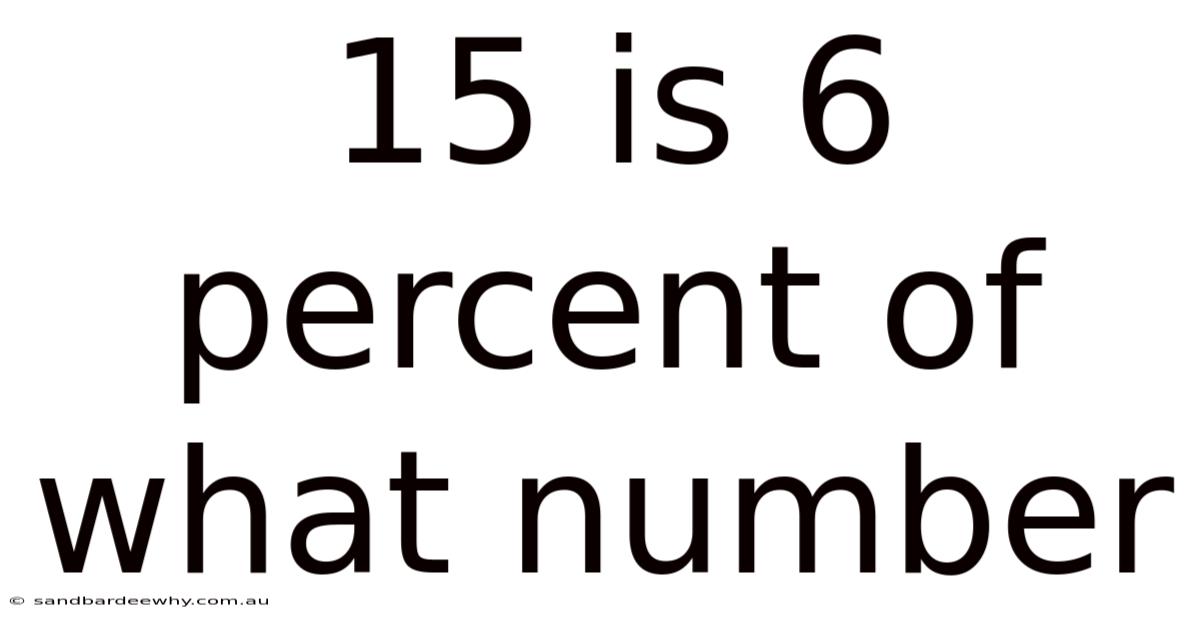
Table of Contents
Imagine you are at a bustling farmer's market, eyeing a beautiful hand-woven basket. The vendor tells you it's 15% off, and the discount comes out to $6. You're suddenly curious: what was the original price of the basket before the discount? This everyday scenario highlights the importance of understanding percentage problems and how to solve them efficiently.
Percentage calculations are a fundamental skill that touches nearly every aspect of our lives. From calculating discounts while shopping to understanding interest rates on loans, percentages are indispensable tools. One common type of percentage problem is finding the whole number when a percentage and its corresponding part are known. The question "15 is 6 percent of what number?" falls into this category. Mastering these calculations not only empowers you in daily financial decisions but also strengthens your analytical thinking.
Decoding Percentage Problems
At its core, a percentage represents a proportion or ratio out of 100. The word "percent" itself comes from the Latin per centum, meaning "out of one hundred." Thus, 6 percent (6%) signifies 6 out of every 100 units. When we say "15 is 6 percent of what number," we are essentially stating that 15 represents 6/100 of an unknown quantity.
To dissect this further, let's define some key terms:
- Percentage: A rate, number, or amount, expressed as parts of a hundred.
- Base: The whole or the total amount to which the percentage refers. This is the unknown number we are trying to find.
- Part: The portion of the base that the percentage represents. In our problem, this is 15.
The relationship between these terms can be expressed through the following formula:
Part = Percentage × Base
In our case, we know the Part (15) and the Percentage (6%), and we need to find the Base. To do this, we can rearrange the formula:
Base = Part / Percentage
This simple formula is the key to unlocking a wide array of percentage-related problems.
The concept of percentages has ancient roots. Even before the formal development of the percentage symbol (%), civilizations used fractions and ratios to express proportions. The Romans, for example, used fractions like 1/100 to calculate taxes on goods sold at auction. However, the widespread use of percentages as we know them today began to emerge during the Renaissance, as trade and commerce flourished in Europe.
As mathematical notations evolved, so did the symbol for percentage. The symbol "%" is believed to have originated from a scribal abbreviation of the Italian term per cento. Over time, this abbreviation evolved into the symbol we use today. The development of standardized mathematical notations, including percentages, was crucial for facilitating complex calculations and ensuring consistency in financial and statistical analyses.
Understanding the historical development of percentages provides context for their importance in modern mathematics and everyday life. Percentages are not merely abstract numbers; they are practical tools that help us make sense of the world around us. Whether you're calculating discounts, analyzing data, or understanding financial reports, a solid grasp of percentages is essential.
Trends and Latest Developments
The use of percentages is not static; it evolves with societal and technological changes. In today's data-driven world, percentages are more relevant than ever. Here are some notable trends and developments:
-
Data Analysis: Percentages are extensively used in statistical analysis to represent proportions, changes, and comparisons within datasets. Whether it's market research, scientific studies, or economic forecasting, percentages help in simplifying complex data and making it more understandable.
-
Financial Technology (FinTech): FinTech companies heavily rely on percentage calculations for various applications, including algorithmic trading, risk assessment, and personalized financial advice. Machine learning algorithms often use percentages to identify patterns and make predictions in financial markets.
-
E-commerce and Retail: Online retailers use percentages to display discounts, calculate sales tax, and offer promotional deals. Understanding how these percentages are applied is crucial for consumers to make informed purchasing decisions.
-
Healthcare: In healthcare, percentages are used to express statistics related to disease prevalence, treatment success rates, and patient outcomes. This information is vital for public health planning and individual healthcare management.
-
Education: Educators use percentages to grade assignments, assess student performance, and track academic progress. Understanding how grades are calculated as percentages helps students and parents gauge academic achievements.
From a professional standpoint, it is important to stay updated with the latest tools and techniques for working with percentages. Spreadsheet software like Microsoft Excel and Google Sheets offers powerful functions for percentage calculations, data analysis, and visualization. Additionally, understanding statistical software packages such as R or Python can provide more advanced capabilities for analyzing and interpreting percentage-based data.
Furthermore, being aware of common misinterpretations or biases related to percentages is essential. For example, a percentage increase followed by an equal percentage decrease does not result in the original value. This is because the percentage decrease is calculated based on the increased value, leading to a lower final result. Such nuances highlight the importance of critical thinking when working with percentages.
Tips and Expert Advice
Solving percentage problems can be straightforward if you follow a systematic approach. Here are some practical tips and expert advice:
-
Understand the Problem: Before attempting to solve a percentage problem, make sure you understand what it's asking. Identify the knowns (percentage and part) and the unknown (base). Translating the word problem into a mathematical equation is a crucial first step.
For example, in the question "15 is 6 percent of what number?" identify that 15 is the part, 6% is the percentage, and we are looking for the base or the whole number. Visualizing the problem can sometimes help. Imagine a pie chart where 6% of the pie represents 15 units. We need to find the total size of the pie.
-
Convert Percentages to Decimals: To perform calculations, convert the percentage to its decimal equivalent by dividing it by 100. This simplifies the process and reduces the risk of errors.
In our example, 6% becomes 6/100 = 0.06. Using the decimal form in calculations makes the math more manageable. Many calculators have a percentage key, but it's still good practice to understand the conversion process.
-
Use the Formula: Apply the formula Base = Part / Percentage. Plug in the known values and solve for the unknown.
Using our example, Base = 15 / 0.06. Performing this division gives us the base. This step requires careful attention to detail to avoid calculation errors.
-
Check Your Answer: After finding the base, verify your answer by multiplying it by the percentage. The result should equal the part. This step helps ensure the accuracy of your calculation.
Once you have the base, multiply it by 0.06. If the result is 15, your answer is correct. This verification step is especially important in real-world scenarios where accuracy is critical.
-
Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations. Work through a variety of problems to build your skills and confidence.
Practice problems can range from simple calculations to more complex scenarios involving discounts, interest rates, and statistical analysis. Online resources, textbooks, and worksheets can provide a wealth of practice material. Regular practice reinforces your understanding and improves your speed and accuracy.
Real-World Examples:
-
Calculating the Original Price: A store offers a 20% discount on a jacket, and the discount amount is $25. What was the original price of the jacket?
- Part = $25
- Percentage = 20% = 0.20
- Base = Part / Percentage = $25 / 0.20 = $125
The original price of the jacket was $125.
-
Determining Sales Tax: You buy an item for $80, and the sales tax is 8%. What is the amount of sales tax?
- Base = $80
- Percentage = 8% = 0.08
- Part = Base × Percentage = $80 × 0.08 = $6.40
The amount of sales tax is $6.40.
-
Analyzing Survey Results: A survey shows that 60% of respondents prefer product A, and 40% prefer product B. If 300 people were surveyed, how many people prefer product A?
- Base = 300
- Percentage = 60% = 0.60
- Part = Base × Percentage = 300 × 0.60 = 180
180 people prefer product A.
FAQ
Q: How do I convert a percentage to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 25% = 25/100 = 1/4.
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase is the relative increase in a value, while percentage decrease is the relative decrease. The formulas are:
- Percentage Increase = ((New Value - Old Value) / Old Value) × 100
- Percentage Decrease = ((Old Value - New Value) / Old Value) × 100
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an original value, and the new value is more than double the original. For example, if a company's revenue increases from $100,000 to $250,000, the percentage increase is 150%.
Q: How do I calculate the percentage difference between two numbers?
A: To calculate the percentage difference between two numbers, use the formula:
Percentage Difference = (|Value 1 - Value 2| / ((Value 1 + Value 2) / 2)) × 100
This formula calculates the absolute difference between the two values and divides it by the average of the two values.
Q: What are some common mistakes to avoid when working with percentages?
A: Common mistakes include:
- Forgetting to convert percentages to decimals before performing calculations.
- Misinterpreting the base in percentage problems.
- Incorrectly applying percentage increase or decrease formulas.
- Not checking the answer to ensure accuracy.
Conclusion
Understanding how to solve percentage problems, like "15 is 6 percent of what number," is a crucial skill with wide-ranging applications in daily life and professional settings. By understanding the basic formula (Base = Part / Percentage) and practicing regularly, you can confidently tackle these calculations. Whether you're calculating discounts, analyzing data, or making financial decisions, a solid grasp of percentages empowers you to make informed choices.
Ready to put your knowledge to the test? Try solving similar percentage problems and share your solutions with friends or colleagues. Consider exploring more advanced percentage calculations and their applications in finance, statistics, and other fields. The more you engage with percentages, the more confident and proficient you'll become in using them.
Latest Posts
Latest Posts
-
How Many Grams Are In 250 Ml
Nov 27, 2025
-
How To Find Mean From Histogram
Nov 27, 2025
-
48 Oz Equals How Many Pounds
Nov 27, 2025
-
How Do You Write A Decimal As A Mixed Number
Nov 27, 2025
-
How Many Months Have Exactly 30 Days
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about 15 Is 6 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.