19 Out Of 25 As A Percent
sandbardeewhy
Nov 23, 2025 · 12 min read
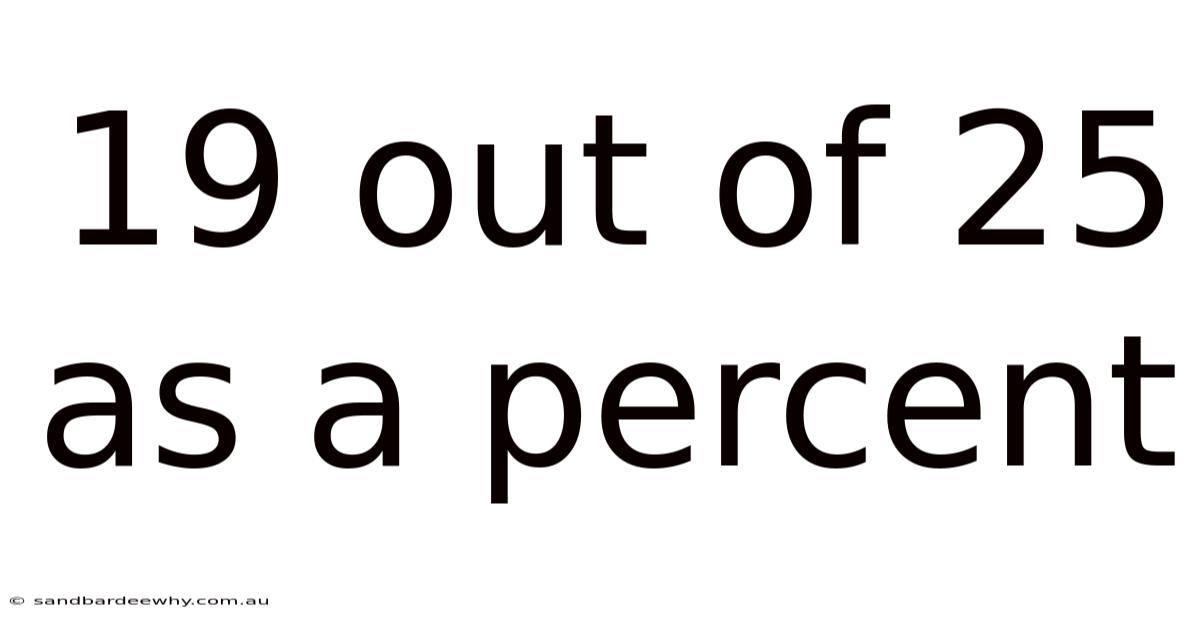
Table of Contents
Imagine you're at a carnival, playing a ring toss game. You get 25 chances to win a giant teddy bear, and you successfully land the ring on a bottle 19 times. How would you figure out your winning percentage to brag to your friends? Or perhaps you're a teacher grading papers. A student gets 19 out of 25 questions right on a test. What percentage grade do you assign them? These scenarios all boil down to understanding how to express a fraction as a percentage, and it's a surprisingly useful skill in everyday life.
Calculating 19 out of 25 as a percent is a fundamental math skill that finds applications in various real-world scenarios, from understanding exam scores to figuring out discounts at your favorite store. A percentage is simply a way of expressing a number as a fraction of 100. Understanding how to convert fractions to percentages, specifically 19/25 in this instance, will equip you with a valuable tool for interpreting data and making informed decisions. In this article, we'll delve into the process, exploring the underlying concepts, practical applications, and some expert tips to make this calculation second nature.
Main Subheading: Understanding the Basics of Percentages
Percentages are a ubiquitous part of modern life. From sales and taxes to statistical data and academic grading, they provide a standardized way to represent proportions and ratios. Understanding the basic principles behind percentages is crucial for interpreting information accurately and making sound judgments. The term "percent" comes from the Latin per centum, meaning "out of one hundred." This etymology highlights the core concept: a percentage is a fraction with a denominator of 100. Therefore, expressing a number as a percentage involves scaling it to fit within this framework.
At its core, a percentage is a dimensionless number, meaning it doesn't have any units associated with it. It simply represents a ratio or a proportion. For example, if you say that 80% of students passed an exam, you are indicating that 80 out of every 100 students achieved a passing grade. The beauty of using percentages lies in their ability to provide a standardized way to compare different quantities. This is especially useful when dealing with data sets that have different scales or units of measurement. The process of converting a fraction to a percentage involves transforming the fraction into an equivalent fraction with a denominator of 100. Once this transformation is complete, the numerator represents the percentage. This simple yet powerful concept underpins a wide range of applications, making it an indispensable tool for anyone seeking to understand and interpret quantitative information.
Comprehensive Overview of Converting Fractions to Percentages
Converting fractions to percentages is a fundamental mathematical operation with wide-ranging practical applications. The underlying principle is to express the fraction as an equivalent fraction with a denominator of 100, which directly translates to the percentage value. This conversion can be achieved through several methods, each offering its own advantages depending on the specific fraction in question. One of the most straightforward methods involves directly multiplying the fraction by 100%. This approach works because multiplying by 100 effectively scales the fraction to represent a value out of 100, which is the definition of a percentage.
For example, to convert the fraction 19/25 to a percentage, you would multiply it by 100%: (19/25) * 100% = 76%. Another approach involves finding a factor that, when multiplied by the denominator of the fraction, results in 100. Once this factor is identified, you multiply both the numerator and the denominator by it. This method is particularly useful when the denominator is a factor of 100, as it simplifies the conversion process. In the case of 19/25, since 25 * 4 = 100, you can multiply both the numerator and denominator by 4: (19 * 4) / (25 * 4) = 76/100, which directly translates to 76%.
A third method, and perhaps the most universally applicable, involves dividing the numerator by the denominator to obtain a decimal value, and then multiplying the decimal by 100%. This method works for any fraction, regardless of whether the denominator is a factor of 100. For example, if you had a fraction like 7/13, you would divide 7 by 13 to get approximately 0.5385, and then multiply by 100% to get 53.85%. Understanding these methods allows for flexibility in approaching fraction-to-percentage conversions, enabling you to choose the most efficient approach based on the specific numbers involved. Whether you are calculating a simple fraction like 1/2 or a more complex one like 17/32, these techniques provide a reliable framework for accurate conversion.
The historical roots of percentages can be traced back to ancient Rome, where calculations involving hundredths were used for taxation and commerce. However, the widespread use of the percent symbol (%) is a more recent development, dating back to the 15th century. Over time, percentages have become an indispensable tool in mathematics, statistics, and finance, enabling standardized comparisons and simplifying complex calculations. The concept of a percentage is closely related to that of a ratio, which expresses the relative size of two quantities. However, percentages offer the advantage of being normalized to a scale of 100, making it easier to compare proportions across different contexts. Understanding the mathematical foundations of percentages, including their relationship to fractions, ratios, and decimals, is essential for mastering this versatile tool. By grasping the underlying principles, you can confidently apply percentages in a wide range of real-world situations, from calculating discounts to analyzing statistical data.
In addition to the basic methods of conversion, there are several nuances to consider when working with percentages. For example, when dealing with mixed numbers or improper fractions, it is often helpful to convert them to improper fractions before applying the percentage conversion methods. This ensures that the calculations are accurate and consistent. It's also important to be mindful of rounding errors when working with decimals, especially when the percentage value has many decimal places. In such cases, it's best to round the percentage to an appropriate level of precision based on the context of the problem. Furthermore, understanding the relationship between percentages and other mathematical concepts, such as proportions and ratios, can provide deeper insights into the underlying data. For example, if you know that a certain quantity represents 30% of a whole, you can use proportions to calculate the value of the whole or the value of other parts.
Trends and Latest Developments Involving Percentages
While the fundamental concept of percentages remains constant, their application and interpretation are constantly evolving, driven by trends in data analysis, technology, and consumer behavior. One notable trend is the increasing emphasis on data visualization, where percentages are used to create charts and graphs that communicate complex information in an accessible manner. Tools like pie charts, bar graphs, and heatmaps often rely on percentages to represent proportions and distributions, allowing viewers to quickly grasp key insights. In the field of finance, percentages are used extensively to analyze investment returns, calculate interest rates, and assess risk. With the rise of algorithmic trading and machine learning, sophisticated models are being developed to predict market trends and optimize investment strategies based on percentage-based indicators.
Another emerging trend is the use of personalized percentages in marketing and customer service. Companies are leveraging data analytics to understand individual customer preferences and tailor their offerings accordingly. For example, a retailer might offer a personalized discount of 15% off a customer's favorite product category, based on their past purchase history. This level of customization requires sophisticated data processing and analysis, but it can lead to increased customer satisfaction and loyalty. In the realm of education, percentages are increasingly being used to track student progress and identify areas where students may need additional support. Adaptive learning platforms use algorithms to assess a student's understanding of different concepts and provide personalized instruction based on their performance. Percentages play a key role in this process, allowing educators to monitor student progress and adjust their teaching strategies accordingly.
Moreover, the rise of social media and online advertising has led to a greater focus on metrics like click-through rates (CTR) and conversion rates, which are often expressed as percentages. These metrics are used to evaluate the effectiveness of online campaigns and optimize marketing strategies. Understanding how to interpret and analyze these percentage-based metrics is essential for anyone involved in digital marketing or advertising. As technology continues to evolve, the ways in which percentages are used and interpreted will continue to adapt. From data visualization to personalized marketing, percentages will remain a fundamental tool for understanding and communicating quantitative information. Staying abreast of these trends and developments is crucial for anyone seeking to leverage the power of percentages in their professional or personal lives.
Tips and Expert Advice for Calculating and Using Percentages
Mastering the calculation and application of percentages requires more than just understanding the basic formulas. Here are some expert tips and advice to help you become proficient in using percentages in various contexts:
-
Understand the Base: One of the most common mistakes when working with percentages is misunderstanding the base value. Always clarify what the percentage is of. For example, a 20% discount on a $100 item means you're taking 20% of $100, which is $20. The new price is then $100 - $20 = $80. However, if the item is marked up by 20% and then discounted by 20%, you won't end up back at the original price. The markup is calculated on the original price, while the discount is calculated on the increased price. This highlights the importance of clearly identifying the base value in each calculation.
-
Use Mental Math Tricks: Developing mental math skills can significantly speed up percentage calculations. For example, knowing that 10% of a number is simply the number divided by 10 allows you to quickly calculate multiples of 10%. To find 20%, double the 10% value. To find 5%, halve the 10% value. Similarly, knowing that 25% is equivalent to 1/4 and 50% is equivalent to 1/2 can simplify calculations involving these percentages. Practice these mental math tricks regularly to improve your speed and accuracy.
-
Estimate Before Calculating: Before performing a percentage calculation, take a moment to estimate the answer. This will help you catch any obvious errors in your calculations. For example, if you're calculating 76% of 120, you know that the answer should be slightly more than 75% of 120, which is 90 (since 75% = 3/4). If your calculated answer is significantly different from this estimate, you know that you've made a mistake somewhere.
-
Pay Attention to Rounding: When working with decimals, be mindful of rounding errors. Depending on the context of the problem, it may be necessary to round the percentage to an appropriate level of precision. For example, if you're calculating sales tax, you typically round to the nearest cent. However, if you're calculating investment returns, you may need to use more decimal places to accurately reflect the value of your investments. Always consider the implications of rounding and choose the appropriate level of precision based on the specific situation.
-
Use Technology Wisely: While mental math and manual calculations are valuable skills, technology can also be a useful tool for working with percentages. Calculators, spreadsheets, and online percentage calculators can help you perform complex calculations quickly and accurately. However, it's important to understand the underlying principles behind these tools and not rely on them blindly. Always double-check your results and make sure that they make sense in the context of the problem.
-
Practice with Real-World Examples: The best way to master percentages is to practice with real-world examples. Look for opportunities to use percentages in your everyday life, whether it's calculating discounts at the store, figuring out tips at a restaurant, or analyzing statistical data in the news. The more you practice, the more comfortable you'll become with using percentages and the more easily you'll be able to apply them in different situations.
FAQ About Calculating Percentages
Q: What is the formula for calculating a percentage?
A: The basic formula for calculating a percentage is: (Part / Whole) * 100%. The "part" is the specific amount you're interested in, and the "whole" is the total amount.
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, simply multiply the decimal by 100%. For example, 0.75 * 100% = 75%.
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase or decrease, use the following formula: ((New Value - Old Value) / Old Value) * 100%. A positive result indicates an increase, while a negative result indicates a decrease.
Q: What's the difference between a percentage point and a percentage?
A: A percentage point is the simple difference between two percentages. For example, if a rate increases from 10% to 12%, that's a 2 percentage point increase. It's not a 2% increase; it's a 20% increase (2/10 * 100%) of the original percentage.
Q: How do I calculate the original value if I know the percentage and the result?
A: If you know the percentage and the result, you can calculate the original value by dividing the result by the percentage (expressed as a decimal). For example, if 20% of a number is 50, the original number is 50 / 0.20 = 250.
Conclusion
Converting 19 out of 25 to a percentage is a straightforward calculation that results in 76%. However, the broader understanding of percentages and their applications is a skill that can significantly enhance your ability to interpret data and make informed decisions in various aspects of life. By mastering the concepts, practicing regularly, and staying aware of current trends, you can confidently use percentages to solve problems and gain valuable insights. Now that you've armed yourself with this knowledge, take the next step and apply it in your daily life. Whether it's calculating discounts, analyzing statistics, or simply understanding the world around you, percentages will be a valuable tool in your arsenal. Start practicing today, and you'll quickly find that percentages are not just a mathematical concept but a powerful way to understand and navigate the world.
Latest Posts
Latest Posts
-
What Do You Call A Thai Person
Nov 23, 2025
-
How Much Is 64 Oz In Liters
Nov 23, 2025
-
How Many Nickels Are In 17
Nov 23, 2025
-
How Do You Say Close In Spanish
Nov 23, 2025
-
What Is 15 Out Of 75 As A Percent
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about 19 Out Of 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.