2 Divided By 3 As A Fraction
sandbardeewhy
Nov 23, 2025 · 12 min read
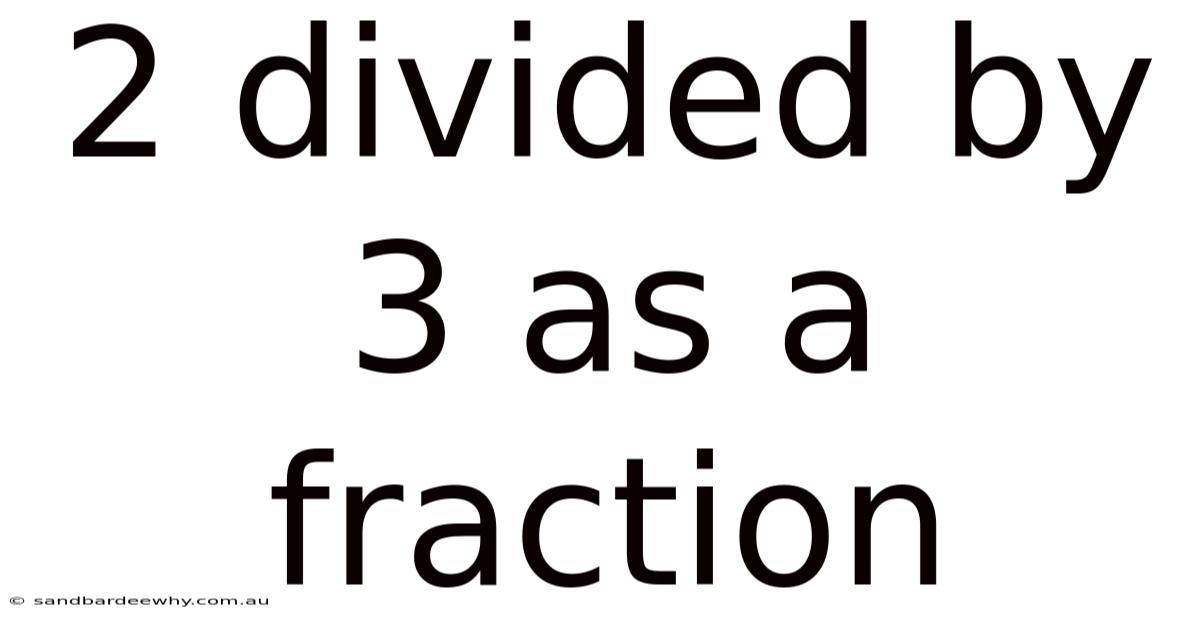
Table of Contents
Have you ever tried dividing a pizza with two friends? Or splitting two cookies equally? These everyday scenarios introduce us to the concept of fractions, and sometimes, the answer isn't a whole number. Instead, it’s a part of a whole, beautifully represented as a fraction. Understanding how to express divisions like "2 divided by 3" as a fraction unlocks a fundamental aspect of mathematics and is surprisingly useful in daily life.
Imagine you have two delicious chocolate bars, and you want to share them fairly with three people. How much does each person get? The answer, in its simplest form, is a fraction. This seemingly simple division problem, 2 divided by 3 as a fraction, forms the basis of many mathematical concepts. This article will dive deep into understanding fractions, the concept of division as a fraction, and how to easily and confidently work with fractions in different contexts.
Main Subheading
Fractions are more than just numbers written one above the other with a line in between. They are a fundamental part of mathematics, used to represent parts of a whole, ratios, and division. In essence, a fraction tells us how many parts of a whole we have. The beauty of fractions lies in their ability to express quantities that are not whole numbers, allowing for precision and accuracy in calculations and representations. Without fractions, we'd struggle to accurately describe things like half a cake, a quarter of an hour, or even the precise measurements in a recipe.
Understanding fractions opens up a world of possibilities in mathematics and beyond. From basic arithmetic to advanced calculus, fractions are used everywhere. Learning how to work with them confidently empowers us to solve a wide range of problems in everyday life, from splitting bills with friends to understanding financial reports. This understanding also serves as a foundation for more complex mathematical concepts such as ratios, proportions, and percentages, making it an essential skill for anyone looking to enhance their mathematical abilities.
Comprehensive Overview
At its core, a fraction represents a part of a whole. It is written in the form of a/b, where a is the numerator and b is the denominator. The numerator (a) tells us how many parts we have, while the denominator (b) tells us the total number of equal parts that make up the whole. For example, in the fraction 1/2, the numerator (1) indicates that we have one part, and the denominator (2) indicates that the whole is divided into two equal parts.
The concept of 2 divided by 3 as a fraction arises from the understanding that division can be represented as a fraction. When we divide 2 by 3, we are essentially asking: What fraction of 3 is 2? The answer, quite simply, is 2/3. The number being divided (2 in this case) becomes the numerator, and the number we are dividing by (3) becomes the denominator. This relationship between division and fractions is fundamental and allows us to express division problems in a more versatile and understandable way.
Fractions can be classified into different types based on the relationship between the numerator and denominator:
- Proper Fractions: These are fractions where the numerator is less than the denominator (e.g., 1/2, 2/3, 3/4). Proper fractions represent a value less than one whole.
- Improper Fractions: These are fractions where the numerator is greater than or equal to the denominator (e.g., 3/2, 5/4, 7/7). Improper fractions represent a value greater than or equal to one whole.
- Mixed Numbers: These consist of a whole number and a proper fraction (e.g., 1 1/2, 2 1/4, 3 2/5). Mixed numbers are another way to represent values greater than one whole. For instance, 1 1/2 is equivalent to the improper fraction 3/2.
Converting between improper fractions and mixed numbers is a useful skill. To convert an improper fraction to a mixed number, you divide the numerator by the denominator. The quotient becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part, with the original denominator remaining the same. For example, to convert 5/4 to a mixed number, you divide 5 by 4, which gives a quotient of 1 and a remainder of 1. Therefore, 5/4 is equal to 1 1/4.
Fractions can also be simplified, or reduced, to their simplest form. This involves dividing both the numerator and the denominator by their greatest common factor (GCF). For example, the fraction 4/6 can be simplified by dividing both the numerator and the denominator by their GCF, which is 2. This gives us the simplified fraction 2/3. Simplifying fractions makes them easier to work with and understand, especially when performing calculations. In the case of 2 divided by 3 as a fraction, which is 2/3, the fraction is already in its simplest form because 2 and 3 have no common factors other than 1.
Understanding equivalent fractions is also crucial. Equivalent fractions are fractions that represent the same value, even though they have different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions because they both represent half of a whole. To find equivalent fractions, you can multiply or divide both the numerator and the denominator by the same non-zero number. This principle is essential when adding or subtracting fractions with different denominators, as you need to find a common denominator to perform the operation. The ability to identify and create equivalent fractions provides a flexible and powerful tool for working with fractions in various mathematical contexts.
Trends and Latest Developments
Fractions, though a fundamental concept, continue to evolve in their application and understanding, particularly with the rise of technology and data analysis. In recent years, there's been a renewed focus on making fractions more accessible and intuitive for learners of all ages. Educational platforms and apps are now incorporating interactive visuals and gamified approaches to help students grasp the concept of fractions more effectively. This shift towards visual and interactive learning is making fractions less abstract and more relatable to real-world scenarios.
Data analysis and statistical modeling increasingly rely on fractional representations for precision. For instance, in financial markets, fractional shares allow investors to own a portion of a company's stock, regardless of its price. This concept extends to various fields, where proportions and ratios are crucial for decision-making and resource allocation. The ability to express and manipulate fractions accurately is becoming increasingly valuable in these data-driven environments.
The use of fractions in computer science and programming is also notable. While computers primarily operate using binary numbers, fractions play a crucial role in representing real numbers and performing calculations involving decimal values. Understanding fractions helps programmers write more efficient and accurate code for applications that require precise numerical computations. Furthermore, fractions are essential in algorithms related to image processing, data compression, and various forms of scientific simulations.
Fractional calculus, a generalization of traditional calculus, is an area of ongoing research and development. It extends the concepts of differentiation and integration to non-integer orders, allowing for more precise modeling of complex systems in physics, engineering, and economics. This advanced field leverages the fundamental principles of fractions to solve problems that are difficult or impossible to address using conventional calculus methods.
In educational research, there's a growing emphasis on conceptual understanding rather than rote memorization of procedures when teaching fractions. Studies have shown that students who have a strong conceptual understanding of fractions are better able to apply this knowledge to solve real-world problems and develop a deeper appreciation for mathematics. This approach encourages students to think critically about the meaning of fractions and their relationship to other mathematical concepts.
Tips and Expert Advice
Working with fractions can sometimes feel daunting, but with the right approach and a few helpful tips, it can become much more manageable. Here’s some expert advice to help you navigate the world of fractions with confidence:
-
Visualize Fractions: One of the most effective ways to understand fractions is to visualize them. Use diagrams, such as circles or rectangles, to represent the whole, and then divide them into equal parts to represent the fraction. For example, when thinking about 2 divided by 3 as a fraction (2/3), imagine a pie cut into three equal slices, and you have two of those slices. Visual aids can make abstract concepts more concrete and easier to grasp, particularly for visual learners.
-
Master Equivalent Fractions: Understanding equivalent fractions is crucial for performing operations like addition and subtraction. Always look for opportunities to simplify fractions to their lowest terms before performing any calculations. This will make the numbers smaller and easier to work with. Additionally, knowing how to find a common denominator quickly will streamline the process of adding and subtracting fractions with different denominators. For example, to add 1/4 and 1/3, you need to find a common denominator, which is 12. Convert 1/4 to 3/12 and 1/3 to 4/12, then add them to get 7/12.
-
Practice Regularly: Like any mathematical skill, proficiency with fractions comes with practice. Set aside time each day or week to work on fraction problems. Start with basic exercises and gradually move on to more complex ones. Use online resources, textbooks, or worksheets to find practice problems. The more you practice, the more comfortable and confident you will become in working with fractions.
-
Relate Fractions to Real-World Scenarios: Fractions are everywhere in our daily lives, from cooking and baking to measuring and dividing. Try to identify real-world scenarios where fractions are used, and use those scenarios to practice your fraction skills. For example, if a recipe calls for 1/2 cup of flour and you want to double the recipe, you need to multiply 1/2 by 2, which equals 1 cup. Relating fractions to real-world situations makes them more relevant and meaningful, and it helps you see the practical applications of what you're learning.
-
Understand the Relationship Between Fractions, Decimals, and Percentages: Fractions, decimals, and percentages are all different ways of representing the same thing – a part of a whole. Learning how to convert between these different forms can be very helpful. For example, the fraction 1/2 is equivalent to the decimal 0.5 and the percentage 50%. Knowing these equivalencies can make it easier to solve problems that involve fractions, decimals, and percentages. Use a calculator to practice converting between these forms and to check your work.
FAQ
-
How do I express a division problem as a fraction?
To express a division problem as a fraction, the number being divided (the dividend) becomes the numerator, and the number you are dividing by (the divisor) becomes the denominator. For example, 5 divided by 7 is written as the fraction 5/7.
-
What does 2 divided by 3 as a fraction mean?
2 divided by 3 as a fraction simply means 2/3. It represents two parts out of three equal parts of a whole.
-
How do I simplify a fraction?
To simplify a fraction, divide both the numerator and the denominator by their greatest common factor (GCF). For example, to simplify 4/6, find the GCF of 4 and 6, which is 2. Divide both the numerator and the denominator by 2 to get 2/3.
-
How do I convert an improper fraction to a mixed number?
To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part, with the original denominator remaining the same. For example, to convert 7/3 to a mixed number, divide 7 by 3, which gives a quotient of 2 and a remainder of 1. Therefore, 7/3 is equal to 2 1/3.
-
How do I add fractions with different denominators?
To add fractions with different denominators, you first need to find a common denominator. This is a number that is a multiple of both denominators. Then, convert each fraction to an equivalent fraction with the common denominator. Finally, add the numerators and keep the common denominator. For example, to add 1/4 and 1/6, a common denominator is 12. Convert 1/4 to 3/12 and 1/6 to 2/12, then add them to get 5/12.
-
Can all numbers be expressed as fractions?
Yes, all rational numbers can be expressed as fractions. Rational numbers include integers, which can be expressed as fractions with a denominator of 1 (e.g., 5 = 5/1).
-
Why are fractions important?
Fractions are important because they allow us to represent quantities that are not whole numbers. They are used in many areas of mathematics and in everyday life, such as cooking, measuring, finance, and engineering. Understanding fractions is crucial for developing strong mathematical skills and problem-solving abilities.
Conclusion
In summary, understanding 2 divided by 3 as a fraction, which is 2/3, provides a basic yet powerful foundation for grasping more advanced mathematical concepts. Fractions are essential for representing parts of a whole, performing calculations, and solving problems in various real-world scenarios. By mastering the basics of fractions, including simplifying, converting, and performing operations, you can build confidence in your mathematical abilities and unlock a deeper understanding of the world around you.
Now that you've gained a comprehensive understanding of fractions and division, take the next step and put your knowledge into practice. Try solving some fraction problems, explore real-world applications of fractions, and share your insights with others. Engage in discussions, ask questions, and continue to deepen your understanding. Your journey into the world of fractions is just beginning, and with continued effort and curiosity, you'll be amazed at what you can achieve. Don’t hesitate to seek additional resources and guidance as you continue to explore the fascinating world of mathematics.
Latest Posts
Latest Posts
-
How Many Chapters Are In The Hunger Games
Nov 23, 2025
-
5 Is What Percent Of 30
Nov 23, 2025
-
How Tall In Feet Is 58 Inches
Nov 23, 2025
-
What Does Lord Of The Flies Symbolize
Nov 23, 2025
-
What Does Coda Mean In Music
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about 2 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.