200 Is 10 Percent Of What
sandbardeewhy
Nov 20, 2025 · 12 min read
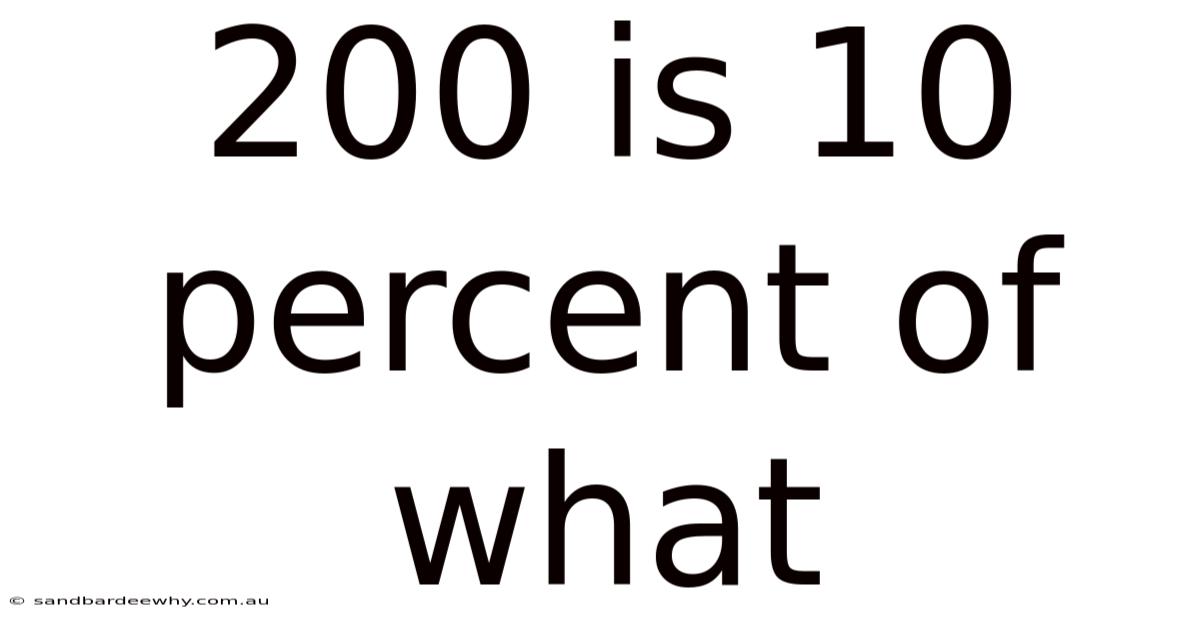
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a basket overflowing with ripe, juicy peaches. The sign declares a "10% off" summer sale. You spot a basket you absolutely must have, now priced at $200. You quickly wonder, "What was the original price of this delightful basket before the discount?" This everyday scenario highlights the practical relevance of understanding percentages and how they relate to finding the whole when only a part is known.
Similarly, consider a scenario in business. A small startup celebrates a successful quarter, announcing that their marketing campaign resulted in a 10% increase in sales, translating to an extra $200 in revenue. To properly evaluate the campaign's true impact and project future growth, they need to know what the total sales were before this 10% boost. Finding the original number, in this case, the original sales figure, is crucial for informed decision-making and strategic planning. This article delves into the simple yet powerful math behind answering the question: "200 is 10 percent of what?" We'll explore the underlying principles, various methods for solving this type of problem, real-world applications, and address some frequently asked questions to solidify your understanding.
Unveiling the Basics: Understanding Percentages
At its core, a percentage is simply a way to express a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." So, when we say 10 percent, we mean 10 out of every 100. This concept is fundamental to a wide array of calculations, from figuring out discounts and taxes to understanding statistics and financial data.
The beauty of percentages lies in their ability to provide a standardized way to compare different proportions. Instead of dealing with various fractions with different denominators, we can convert them all to percentages, making comparisons much easier. For instance, saying that one investment grew by 15% and another by 20% instantly gives you a clear picture of which performed better, without needing to analyze the original investment amounts.
To truly grasp how to solve "200 is 10 percent of what," it's essential to understand the relationship between the percentage, the part, and the whole. In mathematical terms, we can express this relationship as follows:
- Part = Percentage x Whole
Where:
- Part is the specific amount that represents a fraction of the whole. In our question, 200 is the part.
- Percentage is the proportion, expressed as a percentage, that the part represents of the whole. In our question, 10 percent is the percentage.
- Whole is the total or original amount we are trying to find. This is the unknown we need to calculate.
Understanding this equation is the key to unlocking a variety of percentage-related problems. In our specific case, we're given the "Part" (200) and the "Percentage" (10%), and our mission is to find the "Whole." To do this, we need to rearrange the equation to isolate the "Whole."
The concept of percentages dates back to ancient times. The Romans, for instance, used a system similar to percentages when levying taxes on goods sold at auction. However, the modern concept of percentages, with the symbol "%," gained popularity during the Renaissance period. The use of percentages simplified calculations in trade, finance, and various other fields, contributing to their widespread adoption.
The percentage symbol (%) itself is believed to have evolved from a symbol used in manuscripts to denote fractions per one hundred. Over time, this symbol was simplified and eventually became the familiar "%" symbol we use today. Percentages are now an integral part of our daily lives, from calculating tips at restaurants to understanding interest rates on loans.
Methods to Calculate the Whole
Now that we understand the core concept, let's explore different methods to solve the question: "200 is 10 percent of what?"
Method 1: The Algebraic Approach
This method involves translating the problem into an algebraic equation and then solving for the unknown variable. Let's represent the "whole" (the number we're trying to find) with the variable 'x'. We can then rewrite the problem as an equation:
- 10% of x = 200
To work with this equation, we need to convert the percentage into a decimal. To do this, simply divide the percentage by 100:
- 10% = 10 / 100 = 0.10
Now we can substitute this decimal value back into our equation:
-
- 10x = 200
To isolate 'x' and solve for the whole, we need to divide both sides of the equation by 0.10:
- x = 200 / 0.10
- x = 2000
Therefore, 200 is 10 percent of 2000.
This algebraic approach is a powerful and versatile method that can be applied to a wide range of percentage problems. By translating the problem into an equation, we can use the rules of algebra to systematically solve for the unknown variable.
Method 2: The Proportion Method
The proportion method relies on setting up a proportion, which is an equation stating that two ratios are equal. In this case, we know that 200 is to the whole (which we'll call 'x') as 10 is to 100. We can express this as a proportion:
- 200 / x = 10 / 100
To solve for 'x', we can cross-multiply:
- 200 * 100 = 10 * x
- 20000 = 10x
Now, divide both sides by 10 to isolate 'x':
- x = 20000 / 10
- x = 2000
Again, we arrive at the same answer: 200 is 10 percent of 2000.
The proportion method is a useful alternative to the algebraic approach, particularly for those who find visual representations easier to understand. It emphasizes the relationship between the part and the whole as a ratio, making it a clear and intuitive way to solve percentage problems.
Method 3: The Mental Math Trick
For this specific problem, there's a handy mental math trick you can use. If 200 represents 10%, then to find 100% (the whole), you simply need to multiply 200 by 10:
- 200 * 10 = 2000
This works because 100% is ten times larger than 10%. This trick is quick and easy to use in simple scenarios like this one, allowing you to solve the problem in your head without the need for pencil and paper. However, it's important to understand the underlying principles so you can apply the correct method for more complex percentage problems.
This mental math trick is best suited for situations where the given percentage is a simple fraction of 100, such as 10%, 20%, 25%, or 50%. For more complex percentages, the algebraic or proportion methods are generally more reliable.
Real-World Applications of Percentage Calculations
Understanding how to calculate the whole from a percentage and a part has numerous practical applications in various aspects of life and business. Let's explore some examples:
-
Finance: Imagine you receive a stock dividend of $200, which represents a 2% yield on your investment. To determine the total value of your stock holdings, you can use the formula: Total Value = Dividend / Yield. In this case, Total Value = $200 / 0.02 = $10,000. This tells you the original value of your stock investment.
-
Retail: A store is offering a 15% discount on all items. You purchase an item and receive a discount of $30. To find the original price of the item, you can use the formula: Original Price = Discount / Discount Percentage. In this case, Original Price = $30 / 0.15 = $200. This allows you to understand the true savings you're receiving.
-
Sales and Marketing: A company's marketing campaign results in 80 new leads, representing a 5% increase in overall leads. To calculate the total number of leads before the campaign, you can use the formula: Original Leads = New Leads / Percentage Increase. In this case, Original Leads = 80 / 0.05 = 1600. This helps assess the effectiveness of the marketing campaign.
-
Education: A student scores 90 points on a test, which represents 75% of the total possible points. To determine the total points possible on the test, you can use the formula: Total Points = Student's Score / Percentage Score. In this case, Total Points = 90 / 0.75 = 120. This helps the student understand their performance in relation to the overall assessment.
-
Health and Fitness: You lose 5 pounds during a weight loss program, which represents 2.5% of your initial body weight. To calculate your starting weight, you can use the formula: Starting Weight = Weight Loss / Percentage Loss. In this case, Starting Weight = 5 / 0.025 = 200 pounds. This provides a benchmark for tracking your progress.
These are just a few examples of how understanding percentage calculations can be applied in real-world scenarios. Whether you're managing your personal finances, analyzing business data, or simply trying to understand a sale at the store, the ability to calculate the whole from a percentage and a part is a valuable skill.
Tips and Expert Advice for Mastering Percentage Calculations
Percentage calculations can sometimes be tricky, especially when dealing with more complex scenarios. Here are some tips and expert advice to help you master these calculations:
-
Always convert percentages to decimals or fractions before performing calculations. This is a crucial step to avoid errors. Remember to divide the percentage by 100 to convert it to a decimal (e.g., 25% = 0.25) or express it as a fraction (e.g., 25% = 1/4). Failing to do so will lead to inaccurate results.
-
Understand the context of the problem. Before attempting to solve a percentage problem, take the time to understand what the question is asking. Identify the "part," the "percentage," and the "whole." Misinterpreting the question can lead to incorrect solutions. For instance, ensure you know whether you are looking for an increase, decrease, or the original amount.
-
Use estimation to check your answers. Before performing the actual calculation, try to estimate the answer. This will help you determine if your final answer is reasonable. For example, if you're calculating a discount, estimate how much the discount should be and compare it to your calculated answer. If the two values are significantly different, it's a sign that you may have made an error.
-
Practice regularly with different types of problems. The more you practice, the more comfortable you'll become with percentage calculations. Work through a variety of problems involving different scenarios, such as discounts, taxes, interest rates, and percentage changes. This will help you develop a deeper understanding of the concepts and improve your problem-solving skills.
-
Use online calculators and tools to verify your answers. There are many online percentage calculators available that can help you check your work and ensure accuracy. These tools can be particularly useful when dealing with complex calculations or when you want to quickly verify your answers. However, it's important to understand the underlying principles and not rely solely on calculators.
-
Pay attention to the wording of the problem. Percentage problems can sometimes be worded in a way that can be confusing. Pay close attention to the wording of the problem to ensure you understand what is being asked. Look for keywords such as "of," "is," "percent," and "what" to help you identify the different components of the problem.
-
Break down complex problems into smaller, more manageable steps. If you're faced with a complex percentage problem, try breaking it down into smaller, more manageable steps. This will make the problem less daunting and easier to solve. For example, if you're calculating a series of discounts, calculate each discount separately and then combine the results.
FAQ: Frequently Asked Questions About Percentage Calculations
Here are some frequently asked questions about percentage calculations to further clarify your understanding:
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, simply multiply the decimal by 100. For example, 0.75 = 0.75 * 100 = 75%.
Q: How do I calculate a percentage increase?
A: To calculate a percentage increase, use the formula: Percentage Increase = ((New Value - Original Value) / Original Value) * 100. For example, if a price increases from $20 to $25, the percentage increase is ((25-20)/20) * 100 = 25%.
Q: How do I calculate a percentage decrease?
A: To calculate a percentage decrease, use the formula: Percentage Decrease = ((Original Value - New Value) / Original Value) * 100. For example, if a price decreases from $20 to $15, the percentage decrease is ((20-15)/20) * 100 = 25%.
Q: What is the difference between percentage and percentage points?
A: Percentage is a relative measure expressed as a fraction of 100, while percentage points are an absolute difference between two percentages. For example, if an interest rate increases from 5% to 7%, the increase is 2 percentage points, or a 40% increase in the interest rate itself.
Q: How do I calculate a percentage of a percentage?
A: To calculate a percentage of a percentage, first convert both percentages to decimals, then multiply them together. For example, to find 20% of 50%, first convert them to decimals: 0.20 and 0.50. Then multiply: 0.20 * 0.50 = 0.10. Finally, convert the result back to a percentage: 0.10 * 100 = 10%. So, 20% of 50% is 10%.
Conclusion
Mastering the art of percentage calculations, like finding the whole when given a part and a percentage, is not just an academic exercise. It's a practical skill that empowers you to make informed decisions in everyday situations, from navigating sales and discounts to understanding financial data and analyzing business trends. This article has provided you with the tools and knowledge to confidently tackle problems like "200 is 10 percent of what?" by exploring different calculation methods, real-world applications, and expert tips.
Now that you have a solid understanding of these concepts, put your knowledge to the test! Try solving various percentage problems and applying these techniques in real-life scenarios. Share your experiences and challenges in the comments below, and let's continue to learn and grow together. Whether you're a student, a business professional, or simply someone looking to improve their financial literacy, mastering percentage calculations is a valuable asset that will serve you well in various aspects of your life.
Latest Posts
Latest Posts
-
Scientific Definition Of Elastic Potential Energy For Kids
Nov 20, 2025
-
All Summer In A Day Theme
Nov 20, 2025
-
How Many Oz To A Gallon
Nov 20, 2025
-
What Is A Group Of Dogs Called
Nov 20, 2025
-
How Many Legs Does A Scorpion Have
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about 200 Is 10 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.