25 Is What Percent Of 50
sandbardeewhy
Nov 23, 2025 · 12 min read
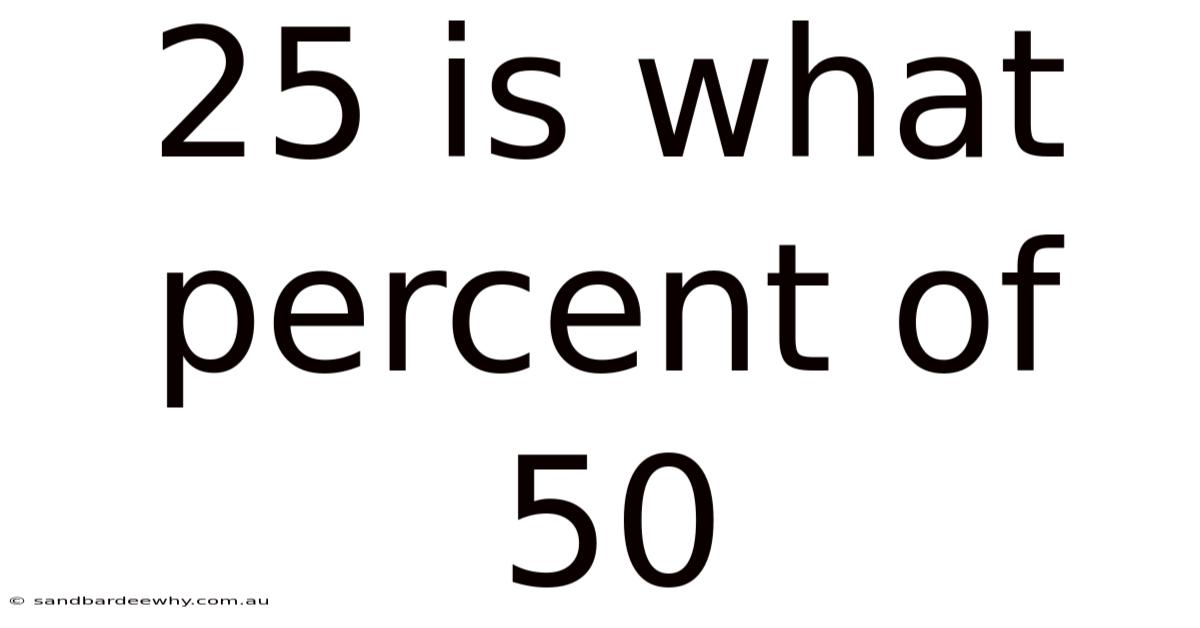
Table of Contents
Imagine you are at a restaurant, and your bill comes to $50. You want to leave a $25 tip. What percentage of the total bill are you tipping? Or perhaps you are tracking your fitness goals and aim to run 50 miles a week. If you've run 25 miles so far, what percentage of your weekly goal have you achieved? These everyday scenarios often require us to calculate what percentage one number represents of another. Understanding how to perform this calculation is not only practical but also a fundamental skill in various aspects of life, from personal finance to academic studies.
The question "25 is what percent of 50?" is a classic percentage problem that demonstrates a core mathematical concept. Percentages are used to express a number as a fraction of 100, providing a standardized way to compare proportions and rates. Whether you're calculating discounts, understanding statistics, or managing budgets, knowing how to solve percentage problems is essential. This article will provide a comprehensive guide to understanding and calculating percentages, focusing specifically on how to determine what percentage 25 is of 50, and will also cover various practical applications and tips to master this skill.
Main Subheading
At its core, the question "25 is what percent of 50?" is a straightforward mathematical problem involving the calculation of percentages. Percentages are a fundamental part of mathematics and are used extensively in everyday life. They provide a standardized way to express proportions, making it easier to understand relationships between numbers. Understanding the basics of percentages is crucial for solving a wide array of problems, from simple calculations to complex statistical analyses.
Before diving into the specific calculation, it's important to understand the underlying concepts. A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred". This means that when we say "X percent," we are referring to X out of 100. For instance, 50 percent means 50 out of 100, or one-half. This concept allows us to compare different quantities relative to a common base, making it easier to understand their proportional relationship.
Comprehensive Overview
To solve the problem "25 is what percent of 50?", we need to understand the formula for calculating percentages. The basic formula is:
Percentage = (Part / Whole) × 100
In this formula:
- Part is the specific quantity we are interested in (in this case, 25).
- Whole is the total or reference quantity (in this case, 50).
Applying this formula to our problem: Percentage = (25 / 50) × 100
First, we divide 25 by 50: 25 / 50 = 0.5
Next, we multiply the result by 100 to convert it to a percentage: 0. 5 × 100 = 50%
Therefore, 25 is 50% of 50.
To truly grasp percentages, understanding their relationship with fractions and decimals is essential. Percentages, fractions, and decimals are different ways of representing the same proportional relationship. For example:
- Percentage: 50%
- Fraction: 50/100, which simplifies to 1/2
- Decimal: 0.5
Converting between these forms is straightforward:
- Percentage to Decimal: Divide the percentage by 100. For example, 50% becomes 50/100 = 0.5.
- Decimal to Percentage: Multiply the decimal by 100. For example, 0.5 becomes 0.5 × 100 = 50%.
- Percentage to Fraction: Write the percentage as a fraction with a denominator of 100 and simplify if possible. For example, 50% becomes 50/100 = 1/2.
- Fraction to Percentage: Convert the fraction to a decimal (by dividing the numerator by the denominator) and then multiply by 100. For example, 1/2 becomes 0.5, and 0.5 × 100 = 50%.
The concept of percentages has ancient roots, with early forms of proportional reasoning dating back to ancient civilizations. However, the modern concept of percentages, as we know it today, emerged during the Middle Ages. Merchants in Italy and other European countries used percentages to calculate profits, interest, and taxes. The use of percentages became more widespread with the development of the decimal system in the 16th century.
Over time, the notation and symbols for percentages evolved. The percent sign (%) is believed to have originated from a symbol used in medieval manuscripts to denote fractions with a denominator of 100. As mathematical practices became standardized, the percent sign became a universal symbol for expressing percentages. Today, percentages are used in almost every field, from finance and economics to science and engineering.
Percentages play a crucial role in many areas of daily life:
- Finance: Understanding interest rates, investment returns, and loan terms requires a solid grasp of percentages. For instance, when comparing different investment options, knowing the percentage return can help you make informed decisions.
- Retail: Discounts, sales tax, and markups are all expressed as percentages. Calculating discounts is a common application of percentage skills. For example, if an item is 20% off, you need to calculate how much money you will save.
- Health and Nutrition: Nutritional information on food labels often includes percentages of daily recommended values. Understanding these percentages helps individuals make healthier food choices.
- Education: Grades are often expressed as percentages, providing a standardized way to evaluate student performance. Understanding how grades are calculated can help students track their progress.
- Statistics: Percentages are used to present and interpret statistical data, making it easier to understand trends and patterns. Whether it's understanding election results or interpreting survey data, percentages are indispensable.
Trends and Latest Developments
In today's data-driven world, the use of percentages is becoming even more sophisticated. Here are some current trends and developments:
- Data Visualization: Percentages are frequently used in data visualization tools to represent proportions and trends. Charts and graphs often use percentages to make data more understandable and accessible. For instance, a pie chart might show the percentage breakdown of a company's expenses.
- Machine Learning and AI: Percentages are used in machine learning algorithms to evaluate model performance. For example, accuracy is often expressed as a percentage of correct predictions. In AI, understanding the certainty or confidence level of a prediction is often crucial, and this is often represented as a percentage.
- E-commerce: Online retailers use percentages extensively for discounts, promotions, and conversion rates. Analyzing conversion rates (the percentage of website visitors who make a purchase) helps businesses optimize their online strategies.
- Financial Analysis: Financial analysts use percentages to analyze company performance, market trends, and investment opportunities. Understanding percentage changes in revenue, profit margins, and stock prices is essential for making informed financial decisions.
According to recent studies, the ability to understand and apply percentages is becoming increasingly important in the workplace. A survey by the National Numeracy Network found that a significant percentage of employers believe that numeracy skills, including the ability to work with percentages, are essential for job success. This highlights the importance of mastering percentage calculations for career advancement.
In recent years, there has been a growing emphasis on financial literacy, which includes understanding percentages. Many educational initiatives and programs aim to improve individuals' ability to make informed financial decisions, and percentages are a core component of these efforts. These programs often focus on practical applications, such as budgeting, saving, and investing.
Professional insights suggest that a strong foundation in percentage calculations can lead to better decision-making in various aspects of life. Financial advisors often emphasize the importance of understanding interest rates and investment returns, both of which involve percentages. Additionally, businesses use percentage analysis to identify areas for improvement and to track progress towards their goals.
Tips and Expert Advice
Mastering percentage calculations involves not only understanding the basic formula but also developing practical skills and strategies. Here are some tips and expert advice to help you improve your percentage proficiency:
- Practice Regularly: Like any mathematical skill, proficiency in percentage calculations requires regular practice. Work through a variety of problems to reinforce your understanding of the concepts. Start with simple problems and gradually progress to more complex ones. Use online resources, textbooks, and worksheets to find practice problems.
- Example: Try calculating percentages in different contexts, such as figuring out discounts at a store or determining the percentage change in your monthly expenses.
- Use Real-World Examples: Applying percentage calculations to real-world scenarios can help you better understand their relevance and usefulness. Think about how percentages are used in everyday situations and try to solve problems related to those situations.
- Example: Calculate the tip you should leave at a restaurant, or determine the percentage of your budget that you spend on housing.
- Break Down Complex Problems: Complex percentage problems can be intimidating, but breaking them down into smaller, more manageable steps can make them easier to solve. Identify the key information and use the appropriate formulas to solve each step.
- Example: If you need to calculate a series of discounts on an item, calculate each discount separately and then combine the results.
- Use Estimation: Estimating the answer before performing the actual calculation can help you check your work and avoid errors. Round the numbers to the nearest whole number or convenient fraction, and then estimate the percentage.
- Example: If you need to calculate 26% of 78, round the numbers to 25% and 80. Then, estimate the answer as 25% of 80, which is 20. This gives you a rough idea of what the actual answer should be.
- Understand Common Percentage Equivalents: Memorizing common percentage equivalents can save you time and effort when performing calculations. Knowing that 25% is equivalent to 1/4 and 50% is equivalent to 1/2 can help you quickly solve many percentage problems.
- Example: If you need to calculate 50% of a number, simply divide the number by 2. If you need to calculate 25% of a number, divide the number by 4.
- Use Technology: Take advantage of technology tools such as calculators and spreadsheets to perform percentage calculations quickly and accurately. These tools can help you solve complex problems and check your work.
- Example: Use a spreadsheet program like Microsoft Excel or Google Sheets to create a percentage calculator. Enter the values and formulas, and the program will automatically calculate the percentage for you.
- Seek Help When Needed: If you are struggling with percentage calculations, don't hesitate to seek help from teachers, tutors, or online resources. Getting clarification on concepts and working through practice problems with a knowledgeable guide can improve your understanding.
- Example: Join a study group or online forum where you can ask questions and get help from other learners.
Financial literacy experts emphasize the importance of understanding percentages for making informed financial decisions. They recommend that individuals develop a strong foundation in percentage calculations to effectively manage their budgets, savings, and investments. By understanding how percentages work, you can better evaluate financial products and services, and make decisions that align with your financial goals.
Businesses use percentage analysis to improve their operations and profitability. By tracking key performance indicators (KPIs) and analyzing percentage changes, businesses can identify areas for improvement and make data-driven decisions. For example, a retail business might track the percentage change in sales from one month to the next to identify trends and adjust its marketing strategies.
FAQ
Q: What is a percentage? A: A percentage is a way of expressing a number as a fraction of 100. The term "percent" means "per hundred," so X percent means X out of 100.
Q: How do I calculate what percentage one number is of another? A: Use the formula: Percentage = (Part / Whole) × 100. The "Part" is the specific quantity you are interested in, and the "Whole" is the total or reference quantity.
Q: How do I convert a percentage to a decimal? A: Divide the percentage by 100. For example, 75% becomes 75/100 = 0.75.
Q: How do I convert a decimal to a percentage? A: Multiply the decimal by 100. For example, 0.25 becomes 0.25 × 100 = 25%.
Q: How do I convert a fraction to a percentage? A: Convert the fraction to a decimal by dividing the numerator by the denominator, and then multiply by 100. For example, 1/4 becomes 0.25, and 0.25 × 100 = 25%.
Q: Why are percentages important in daily life? A: Percentages are used in many areas of daily life, including finance, retail, health, education, and statistics. They help us understand proportions, compare quantities, and make informed decisions.
Q: Can I use a calculator to calculate percentages? A: Yes, calculators can be very helpful for calculating percentages quickly and accurately. Most calculators have a percent key (%) that simplifies the calculation.
Q: What are some common mistakes to avoid when calculating percentages? A: Common mistakes include using the wrong formula, confusing the "Part" and "Whole," and forgetting to multiply by 100. Always double-check your work and use estimation to verify your answer.
Conclusion
In summary, understanding how to calculate percentages is a valuable skill that has numerous applications in everyday life. The question "25 is what percent of 50?" is a fundamental example that illustrates the core principles of percentage calculations. By using the formula Percentage = (Part / Whole) × 100, we can easily determine that 25 is 50% of 50. Mastering percentage calculations involves understanding the relationship between percentages, fractions, and decimals, as well as practicing regularly and applying these skills to real-world scenarios.
Now that you have a comprehensive understanding of how to calculate percentages, it's time to put your knowledge to practice. Whether you're managing your personal finances, analyzing data, or simply trying to understand discounts at a store, the ability to work with percentages will empower you to make more informed decisions. Try solving different percentage problems and explore various applications to further enhance your skills. Share this article with friends or colleagues who might benefit from understanding percentages, and leave a comment below with your own tips and tricks for mastering percentage calculations. Let's continue to improve our mathematical skills and apply them to enhance our daily lives.
Latest Posts
Latest Posts
-
How Many Miles Are 50 Km
Nov 23, 2025
-
96 Oz Is How Many Lbs
Nov 23, 2025
-
Lord Of The Flies Summary Of Chapter 6
Nov 23, 2025
-
190 Days Is How Many Months
Nov 23, 2025
-
How To Find The Zeros Of A Function
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.