3 4 Plus 3 4 Equals
sandbardeewhy
Nov 23, 2025 · 17 min read
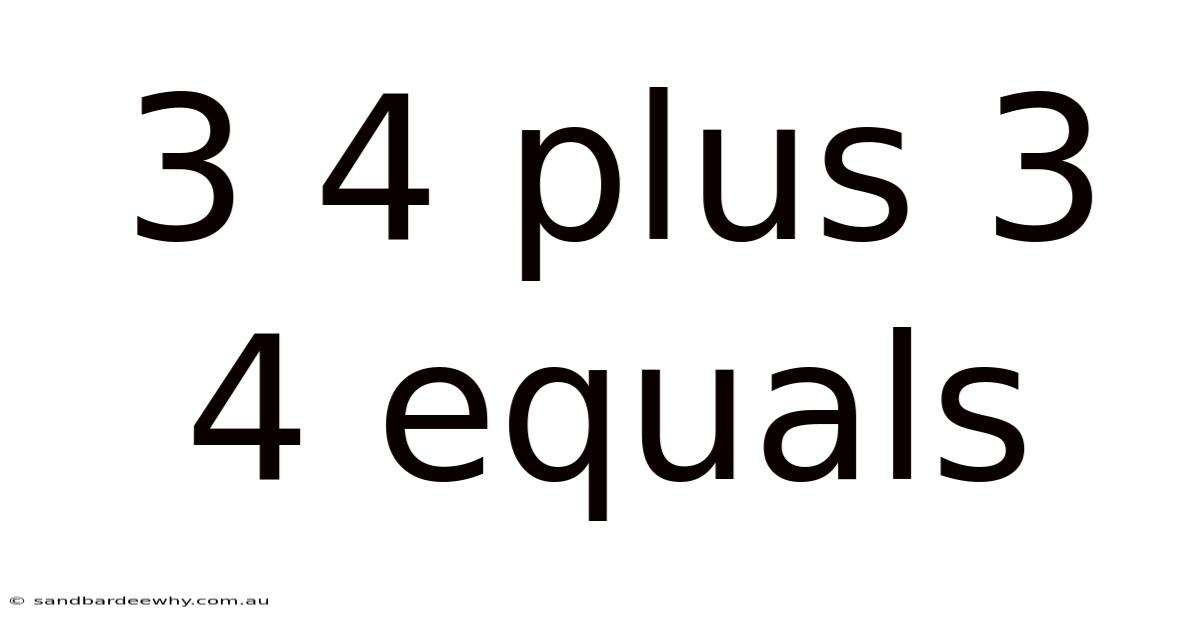
Table of Contents
Imagine baking a pie and the recipe calls for 3/4 cup of sugar, but you decide to double the sweetness. Suddenly, you're faced with a bit of math: what is 3/4 plus 3/4? This simple question opens up a world of understanding about fractions, addition, and how these concepts apply to everyday life. Whether you're measuring ingredients in the kitchen, calculating distances on a map, or even understanding financial reports, knowing how to add fractions is a fundamental skill.
The idea of adding fractions might seem daunting at first, but breaking it down reveals a clear and logical process. It’s not just about crunching numbers; it’s about understanding how quantities combine and relate to each other. From ancient mathematical texts to modern-day applications in engineering and technology, the principles of fraction addition have been pivotal. In this article, we'll explore everything you need to know about solving 3/4 + 3/4, the underlying math concepts, real-world examples, and even some expert tips to make fraction addition a breeze.
Main Subheading: Understanding the Basics of Adding Fractions
Adding fractions is a fundamental arithmetic operation that combines two or more fractional quantities into a single quantity. This operation is crucial in various fields, from basic math to advanced engineering. To truly grasp how to add fractions effectively, it's essential to understand the underlying components of a fraction and the principles that govern their addition.
A fraction consists of two main parts: the numerator and the denominator. The numerator represents the number of parts you have, while the denominator represents the total number of equal parts the whole is divided into. For instance, in the fraction 3/4, "3" is the numerator, indicating that we have three parts, and "4" is the denominator, indicating that the whole is divided into four equal parts.
Core Principles of Fraction Addition
Before diving into the specifics of adding 3/4 + 3/4, let's cover the basic rules of fraction addition:
-
Common Denominator: Fractions can only be added directly if they have the same denominator. This means that the whole is divided into the same number of equal parts for each fraction.
-
Adding Numerators: Once the denominators are the same, you simply add the numerators. The denominator remains the same because you're still dealing with the same size parts of the whole.
-
Simplifying the Result: After adding the numerators, the resulting fraction should be simplified to its lowest terms, if possible. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Adding Fractions with Common Denominators
When fractions have a common denominator, the process is straightforward. For example, consider adding 1/5 + 2/5. Both fractions have the same denominator (5), so you add the numerators:
1 + 2 = 3
The resulting fraction is 3/5. This means you're combining one part out of five with two parts out of five, resulting in three parts out of five.
Adding Fractions with Different Denominators
If fractions have different denominators, you need to find a common denominator before adding them. The most common method is to find the least common multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators.
For example, to add 1/3 + 1/4, the denominators are 3 and 4. The LCM of 3 and 4 is 12. To convert each fraction to have a denominator of 12:
- Multiply the numerator and denominator of 1/3 by 4: (1 * 4) / (3 * 4) = 4/12
- Multiply the numerator and denominator of 1/4 by 3: (1 * 3) / (4 * 3) = 3/12
Now you can add the fractions:
4/12 + 3/12 = 7/12
So, 1/3 + 1/4 = 7/12.
Improper Fractions and Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4). A mixed number consists of a whole number and a proper fraction (e.g., 1 1/4).
To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient is the whole number, the remainder is the new numerator, and the denominator stays the same. For example, to convert 5/4 to a mixed number:
5 ÷ 4 = 1 with a remainder of 1
So, 5/4 = 1 1/4.
Conversely, to convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator. The result is the new numerator, and the denominator stays the same. For example, to convert 1 1/4 to an improper fraction:
(1 * 4) + 1 = 5
So, 1 1/4 = 5/4.
Understanding these basics sets the stage for tackling more complex fraction addition problems, including our focus example of 3/4 + 3/4.
Comprehensive Overview: Solving 3/4 + 3/4
Now that we have a solid foundation in fraction addition, let's specifically address how to solve 3/4 + 3/4. This example is straightforward because both fractions already have a common denominator.
Step-by-Step Solution
-
Identify the Common Denominator: In this case, both fractions have a denominator of 4.
-
Add the Numerators: Add the numerators together while keeping the denominator the same:
3 + 3 = 6
So, 3/4 + 3/4 = 6/4.
-
Simplify the Result: The fraction 6/4 is an improper fraction, meaning the numerator is greater than the denominator. To simplify it, convert it to a mixed number:
6 ÷ 4 = 1 with a remainder of 2
Therefore, 6/4 = 1 2/4.
-
Reduce the Fraction (if possible): The fractional part of the mixed number, 2/4, can be further simplified. Both the numerator and denominator are divisible by 2:
2 ÷ 2 = 1 4 ÷ 2 = 2
So, 2/4 simplifies to 1/2.
-
Final Answer: Combining the whole number and the simplified fraction, we get:
1 2/4 = 1 1/2
Therefore, 3/4 + 3/4 = 1 1/2.
Visual Representation
Visualizing fractions can help in understanding the addition process. Imagine a pie cut into four equal slices. The fraction 3/4 represents three of these slices. If you have two portions of 3/4 of the pie, you combine them.
- First portion: 3 slices (3/4)
- Second portion: 3 slices (3/4)
- Combined: 6 slices (6/4)
Since there are only four slices in a whole pie, having six slices means you have one whole pie (4/4) and two additional slices (2/4), which simplifies to one whole pie and a half (1 1/2).
Alternative Approach: Decimal Conversion
Another way to approach this problem is to convert the fractions to decimals, add the decimals, and then convert the result back to a fraction if needed.
-
Convert to Decimals:
- 3/4 = 0.75
-
Add the Decimals:
-
- 75 + 0.75 = 1.5
-
-
Convert Back to Fraction:
-
- 5 = 1 1/2
-
This approach is particularly useful when dealing with more complex fractions or when you prefer working with decimals.
Real-World Examples
To illustrate the practical application of 3/4 + 3/4, consider these scenarios:
-
Cooking: A recipe calls for 3/4 cup of flour, but you want to double the recipe. How much flour do you need?
- 3/4 + 3/4 = 1 1/2 cups of flour.
-
Distance: You need to walk 3/4 of a mile to the store and another 3/4 of a mile to the park. How far will you walk in total?
- 3/4 + 3/4 = 1 1/2 miles.
-
Time: You spend 3/4 of an hour studying math and another 3/4 of an hour studying science. How much time do you spend studying in total?
- 3/4 + 3/4 = 1 1/2 hours.
Common Mistakes to Avoid
- Forgetting to Simplify: Always simplify the resulting fraction to its lowest terms. Leaving the answer as 6/4 or 1 2/4 is not the most simplified form.
- Adding Denominators: A common mistake is to add both the numerators and denominators (e.g., 3/4 + 3/4 = 6/8). Remember, you only add the numerators when the denominators are the same.
- Incorrect Conversion: When converting improper fractions to mixed numbers, ensure you correctly divide the numerator by the denominator and accurately represent the quotient and remainder.
By understanding these steps and avoiding common mistakes, you can confidently solve 3/4 + 3/4 and similar fraction addition problems.
Trends and Latest Developments
While the basic principles of fraction addition have remained constant, the way we teach and apply these concepts has evolved. Modern trends in mathematics education emphasize a deeper, more intuitive understanding of fractions, moving away from rote memorization to conceptual learning.
Current Educational Approaches
-
Visual Aids: Using visual aids such as fraction bars, pie charts, and interactive software to help students visualize and understand fractions. This hands-on approach makes the abstract concept of fractions more concrete and relatable.
-
Real-World Applications: Connecting fraction addition to real-world scenarios to demonstrate its relevance and practical use. Examples include cooking, measuring, and dividing resources, which resonate with students and make learning more engaging.
-
Technology Integration: Incorporating technology through educational apps and online resources that provide interactive exercises and immediate feedback. These tools help students practice and reinforce their understanding of fraction addition.
Data and Research Insights
Recent studies in mathematics education highlight the effectiveness of visual and kinesthetic learning methods in improving students' comprehension of fractions. Research indicates that students who use visual aids and hands-on activities demonstrate a better understanding of fraction concepts and are more successful in solving fraction-related problems.
Moreover, data from standardized tests reveal that students who receive instruction that emphasizes conceptual understanding rather than rote memorization tend to perform better on fraction-related questions. This underscores the importance of teaching the "why" behind the math, not just the "how."
Expert Opinions
Mathematics educators and researchers emphasize the need for a holistic approach to teaching fractions, focusing on building a strong foundation in basic concepts before moving on to more complex operations. Experts recommend:
- Starting with Concrete Examples: Begin with real-world examples and tangible objects to introduce fractions.
- Using Visual Representations: Employ visual aids to help students visualize and understand fractions.
- Encouraging Discussion: Foster classroom discussions to allow students to share their understanding and clarify misconceptions.
- Providing Ample Practice: Offer plenty of opportunities for students to practice fraction addition through various exercises and activities.
Digital Tools and Resources
The rise of digital technology has provided numerous tools and resources for learning and teaching fraction addition. Some popular resources include:
- Khan Academy: Offers free video lessons and practice exercises on fraction addition and other math topics.
- Math Playground: Provides a variety of interactive math games and activities for students of all ages.
- BrainPOP: Features animated educational videos that explain fraction concepts in an engaging and accessible way.
These digital tools can supplement traditional teaching methods and provide students with additional support and practice opportunities.
Future Trends
Looking ahead, the future of fraction education is likely to be shaped by:
- Personalized Learning: Tailoring instruction to meet the individual needs and learning styles of students.
- Adaptive Learning Technologies: Using AI-powered tools that adjust the difficulty level based on student performance.
- Gamification: Incorporating game-like elements into learning activities to increase engagement and motivation.
By staying informed about these trends and developments, educators and students can leverage the latest resources and techniques to enhance their understanding of fraction addition and other math concepts.
Tips and Expert Advice
Mastering fraction addition, including problems like 3/4 + 3/4, involves more than just understanding the basic steps. Here are some expert tips and practical advice to help you improve your skills and avoid common pitfalls:
1. Emphasize Conceptual Understanding
Instead of memorizing rules, focus on understanding why the rules work. For example, when adding fractions with a common denominator, you're essentially combining parts of the same whole. Understanding this concept can help you avoid mistakes like adding the denominators.
Example: Imagine you have 3/4 of a pizza and your friend gives you another 3/4 of a pizza. You're not changing the size of the slices (the denominator stays the same), but you're increasing the number of slices you have (you add the numerators).
2. Use Visual Aids Regularly
Visual aids can make abstract concepts more concrete. Use fraction bars, pie charts, or even draw your own diagrams to visualize fractions and their addition.
Example: For 3/4 + 3/4, draw two circles, each divided into four equal parts. Shade three parts in each circle to represent 3/4. By combining the shaded parts, you can visually see that you have more than one whole circle, which leads to the mixed number 1 1/2.
3. Practice Regularly with Real-World Problems
Apply fraction addition to real-world scenarios to reinforce your understanding and make the math more relevant. This helps you see the practical applications of fraction addition and improves your problem-solving skills.
Example: Suppose you're planning a garden and need to allocate space for different plants. If you want to dedicate 3/4 of your garden to vegetables and another 3/4 to flowers, how much of your garden will be used in total? This real-world problem makes the addition of 3/4 + 3/4 more meaningful.
4. Break Down Complex Problems
When faced with more complex fraction addition problems, break them down into smaller, more manageable steps. This makes the problem less intimidating and easier to solve.
Example: If you need to add 1/2 + 3/4 + 5/8, first find a common denominator for all three fractions (in this case, 8). Then, convert each fraction to have a denominator of 8: 4/8 + 6/8 + 5/8. Finally, add the numerators: 4 + 6 + 5 = 15. The result is 15/8, which can be simplified to the mixed number 1 7/8.
5. Master Simplification Techniques
Always simplify your final answer to its lowest terms. This ensures that you're presenting the fraction in its most concise and understandable form.
Example: After adding 3/4 + 3/4, you get 6/4. Both 6 and 4 are divisible by 2. Dividing both the numerator and denominator by 2 gives you 3/2, which is an improper fraction. Convert it to a mixed number: 1 1/2.
6. Utilize Online Resources and Tools
Take advantage of the many online resources and tools available for practicing fraction addition. These resources offer interactive exercises, step-by-step solutions, and immediate feedback to help you improve your skills.
Example: Websites like Khan Academy, Math Playground, and IXL offer a variety of fraction addition exercises and tutorials. Use these resources to supplement your learning and practice at your own pace.
7. Identify and Correct Common Mistakes
Be aware of common mistakes in fraction addition, such as forgetting to find a common denominator or adding the denominators. By identifying these mistakes, you can avoid them in the future.
Example: A common mistake is to add 1/2 + 1/3 as 2/5. Remember, you need to find a common denominator first. The correct solution is to convert the fractions to 3/6 + 2/6, which equals 5/6.
8. Teach Others
One of the best ways to reinforce your understanding of fraction addition is to teach it to someone else. Explaining the concepts and steps to others forces you to think critically about the material and identify any gaps in your knowledge.
Example: If you have a friend or family member who is struggling with fraction addition, offer to help them. By teaching them how to add fractions, you'll not only reinforce your own understanding but also gain a deeper appreciation for the concepts involved.
By following these tips and expert advice, you can enhance your fraction addition skills and confidently tackle any fraction-related problem.
FAQ: Frequently Asked Questions About Adding Fractions
Q: Why do fractions need to have the same denominator before adding them?
A: Fractions need a common denominator because you can only add or subtract quantities that are measured in the same units. The denominator tells you what size the "unit" is (i.e., how many parts the whole is divided into). If the denominators are different, you're trying to add different-sized pieces, which doesn't give you a meaningful total without converting them to a common size first.
Q: What is an improper fraction, and how do I deal with it?
A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4). To deal with it, you usually convert it to a mixed number. Divide the numerator by the denominator; the quotient is the whole number part, and the remainder becomes the new numerator over the original denominator. For example, 5/4 becomes 1 1/4.
Q: How do I find the least common denominator (LCD) when adding fractions with different denominators?
A: The least common denominator (LCD) is the least common multiple (LCM) of the denominators. To find it, list the multiples of each denominator until you find the smallest multiple they have in common. Alternatively, you can use prime factorization to find the LCM.
Q: Can I use a calculator to add fractions?
A: Yes, many calculators can add fractions. However, it's essential to understand the process yourself so you can estimate answers and check the calculator's result for accuracy. Understanding the underlying principles is more valuable in the long run.
Q: What should I do if my answer is not in the simplest form?
A: Simplify your answer by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example, if your answer is 4/6, the GCD of 4 and 6 is 2. Divide both by 2 to get the simplified fraction 2/3.
Q: Is there a difference between adding fractions and adding mixed numbers?
A: Yes, adding mixed numbers involves an extra step. You can either convert the mixed numbers to improper fractions, add them, and then convert back to a mixed number, or you can add the whole numbers and fractions separately, and then combine them.
Q: What if I'm adding more than two fractions?
A: The same principles apply. Find a common denominator for all fractions, convert each fraction to have that denominator, and then add the numerators. Simplify the result if necessary.
Q: How does adding fractions relate to other math concepts?
A: Adding fractions is foundational for many other math concepts, including algebra, geometry, and calculus. It's essential for understanding ratios, proportions, and percentages, and is used in various real-world applications, from cooking to engineering.
Q: What are some common real-world applications of adding fractions?
A: Real-world applications include:
- Cooking: Adjusting recipes that call for fractional amounts of ingredients.
- Construction: Measuring materials and calculating dimensions.
- Finance: Calculating portions of investments or budgets.
- Time Management: Planning and allocating time for various tasks.
Q: How can I help my child improve their understanding of adding fractions?
A: Use visual aids, real-world examples, and hands-on activities to make the concept more concrete. Encourage practice and provide positive reinforcement. Break down complex problems into smaller steps, and celebrate progress along the way.
Conclusion
In summary, understanding how to add fractions, including the example of 3/4 plus 3/4, is a crucial skill that extends far beyond the classroom. From everyday tasks like cooking and measuring to more complex applications in engineering and finance, the ability to add fractions accurately and efficiently is invaluable.
We've explored the basic principles of fraction addition, including the importance of finding a common denominator, adding numerators, and simplifying the result. We've also delved into visual representations, real-world examples, and expert tips to enhance your understanding and problem-solving skills.
Remember, mastering fraction addition involves more than just memorizing rules. It requires a deep understanding of the underlying concepts and a willingness to practice regularly. By following the tips and advice provided in this article, you can build a strong foundation in fraction addition and confidently tackle any fraction-related challenge.
Now that you have a comprehensive understanding of how to add fractions, including 3/4 + 3/4, take the next step. Practice these concepts regularly, explore additional resources, and challenge yourself with more complex problems. Share this knowledge with others and help them unlock the power of fractions. What real-world problem can you solve today using your newfound skills in adding fractions?
Latest Posts
Latest Posts
-
What Does The Orange Moon Mean
Nov 23, 2025
-
How Many Kg Is 110 Pounds
Nov 23, 2025
-
How Many Gallons In A Cubic Meter
Nov 23, 2025
-
Spanish Words That Start With O
Nov 23, 2025
-
Three Sentences Of How I Can Show An Elliptical Galaxy
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Plus 3 4 Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.