3 Of 15 Is What Percent
sandbardeewhy
Nov 27, 2025 · 9 min read
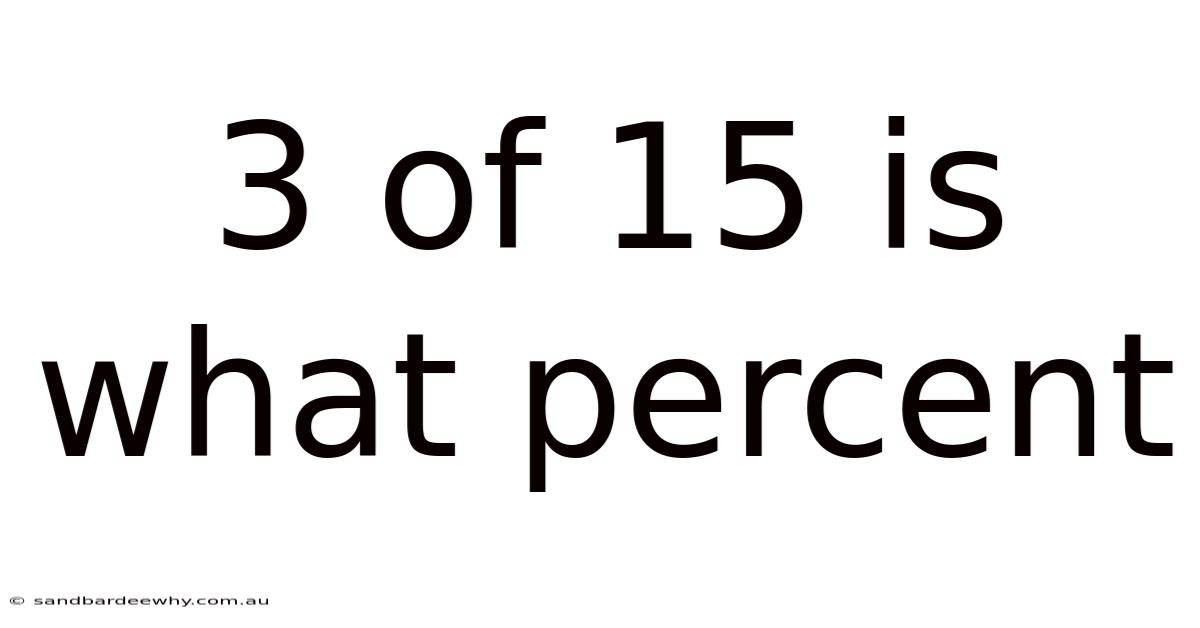
Table of Contents
Imagine you're at a pizza party. There are 15 slices of pizza, and you manage to eat 3 of them. You might wonder, "What portion of the pizza did I devour?" or, more formally, "3 out of 15 is what percent?". This is a common question that we encounter in everyday life, from figuring out discounts at the store to understanding statistics presented in the news.
Whether you are a student grappling with homework, a professional analyzing data, or simply someone trying to make sense of the world around you, understanding how to calculate percentages is an invaluable skill. The question "3 of 15 is what percent?" serves as a gateway to mastering this fundamental mathematical concept. By grasping the principles behind this simple calculation, you'll be well-equipped to tackle more complex percentage-related problems and gain a deeper understanding of numerical relationships.
Main Subheading
Understanding percentages is more than just a mathematical exercise; it's a practical tool that enhances our ability to interpret and interact with the world. Percentages are used everywhere, from calculating interest rates on loans to understanding the results of scientific studies. The ubiquity of percentages in our daily lives underscores the importance of mastering the basic calculations that underpin their use.
The problem "3 of 15 is what percent?" represents a fundamental application of percentage calculations. It's a question that arises in various contexts, from dividing resources to assessing performance. The ability to quickly and accurately determine what percentage one number represents of another is a valuable skill that can save time, reduce errors, and improve decision-making.
Comprehensive Overview
At its core, a percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred". Thus, when we say "x percent," we mean "x out of 100," which can be written as x/100. Percentages provide a standardized way to compare different proportions, making it easier to understand relative sizes and changes.
The concept of percentages dates back to ancient Rome. As the Roman Empire expanded, there was a need for a standardized way to calculate taxes and assess tariffs on goods. The Romans often used fractions based on 100, which laid the groundwork for the modern concept of percentages. However, the widespread use of percentages as we know them today didn't occur until the Middle Ages, when merchants and traders began using them to calculate profits, losses, and interest rates. The introduction of the percent sign (%) in the 17th century further solidified the use of percentages in mathematics and commerce.
To calculate what percentage one number is of another, you can use a simple formula:
Percentage = (Part / Whole) * 100
In this formula:
- Part is the number you want to express as a percentage of the whole.
- Whole is the total or reference value.
- Percentage is the result of the calculation, expressed as a percentage.
Applying this formula to the question "3 of 15 is what percent?":
- Part = 3
- Whole = 15
So, the calculation becomes:
Percentage = (3 / 15) * 100
First, divide 3 by 15:
3 / 15 = 0.2
Then, multiply the result by 100:
- 2 * 100 = 20
Therefore, 3 is 20% of 15.
Understanding the relationship between fractions, decimals, and percentages is crucial for mastering percentage calculations. A fraction represents a part of a whole, and a decimal is another way of expressing a fraction. A percentage is simply a decimal multiplied by 100. For example, the fraction 3/15 can be simplified to 1/5. As a decimal, 1/5 is equal to 0.2, and as a percentage, it's 20%. Being able to convert between these different forms allows for greater flexibility in problem-solving.
Percentages are not just abstract numbers; they have real-world implications. For example, if a store offers a 20% discount on an item, you can calculate the amount of the discount by multiplying the original price by 20% (or 0.2). Similarly, if you want to calculate the sales tax on a purchase, you can multiply the price of the item by the sales tax rate (expressed as a percentage). Understanding percentages allows you to make informed decisions about spending, saving, and investing.
Trends and Latest Developments
In today's data-driven world, percentages are more relevant than ever. From tracking economic indicators to analyzing social media trends, percentages are used to summarize and communicate complex information. According to recent reports, businesses are increasingly relying on data analytics to make strategic decisions, and understanding percentages is a fundamental skill for anyone working in this field.
In education, there is a growing emphasis on teaching practical math skills, including percentage calculations. Educators recognize that students need to be able to apply mathematical concepts to real-world situations, and percentages are a key component of this. New teaching methods and technologies are being developed to help students better understand and master percentage calculations.
Recent surveys indicate that many adults struggle with basic percentage calculations, which can lead to financial errors and poor decision-making. This has prompted a renewed focus on financial literacy and the importance of understanding percentages in personal finance. Online calculators and educational resources have made it easier for people to calculate percentages, but a solid understanding of the underlying concepts is still essential.
The way data is presented is also evolving. Visualizations, such as charts and graphs, are often used to display percentages in a clear and intuitive way. This makes it easier for people to understand trends and patterns in data. However, it's important to be critical of the way percentages are presented, as they can sometimes be used to mislead or distort information.
Tips and Expert Advice
Calculating percentages can be made easier with a few simple tips and tricks. One helpful technique is to break down the percentage into smaller parts. For example, if you need to calculate 15% of a number, you can find 10% by moving the decimal point one place to the left and then find 5% by halving the 10%. Adding these two values together will give you 15%. This approach can be particularly useful for mental calculations.
Another tip is to use benchmarks to estimate percentages. For example, knowing that 25% is equivalent to one-quarter can help you quickly estimate percentages in many situations. If you need to find 25% of 80, you can simply divide 80 by 4 to get 20. Similarly, knowing that 50% is equivalent to one-half can make calculations even easier. These benchmarks can save time and reduce the likelihood of errors.
When dealing with more complex percentage problems, it's helpful to use a calculator or spreadsheet. These tools can perform calculations quickly and accurately, allowing you to focus on the underlying concepts. However, it's important to understand the formulas and principles behind the calculations, even when using technology. This will help you catch errors and ensure that you're using the tools correctly.
In real-world applications, it's important to pay attention to the context of the problem. For example, when calculating discounts, make sure you understand whether the discount is applied before or after taxes. Similarly, when calculating interest rates, be aware of whether the interest is simple or compound. Understanding the context of the problem will help you avoid mistakes and make informed decisions.
Always double-check your work to ensure accuracy. Percentage calculations can be prone to errors, especially when dealing with large numbers or complex formulas. Taking a few extra moments to review your calculations can save you time and frustration in the long run. If possible, use a different method or tool to verify your results.
FAQ
Q: What is a percentage? A: A percentage is a way of expressing a number as a fraction of 100. It is denoted by the percent sign (%).
Q: How do I calculate what percentage one number is of another? A: Use the formula: Percentage = (Part / Whole) * 100
Q: What is the difference between a percentage and a decimal? A: A percentage is a decimal multiplied by 100. For example, 0.2 is equivalent to 20%.
Q: How can I estimate percentages in my head? A: Use benchmarks like 25% (one-quarter) and 50% (one-half) to make quick estimates.
Q: Why is it important to understand percentages? A: Percentages are used in many real-world applications, including finance, retail, and statistics. Understanding percentages allows you to make informed decisions and interpret data accurately.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include using the wrong formula, not paying attention to the context of the problem, and not double-checking your work.
Q: Where can I find resources to help me improve my percentage calculation skills?
A: Many websites and apps offer tutorials, practice problems, and calculators to help you improve your percentage calculation skills.
Q: How are percentages used in everyday life?
A: Percentages are used to calculate discounts, sales tax, interest rates, and statistics, among other things.
Q: Can percentages be greater than 100%?
A: Yes, percentages can be greater than 100% when representing an increase or growth relative to an initial value.
Q: What is the origin of the term "percent"?
A: The term "percent" comes from the Latin per centum, meaning "out of one hundred."
Conclusion
Understanding how to calculate "3 of 15 is what percent?" is a foundational skill that empowers you to make sense of the world around you. By mastering the basic formula and practicing with real-world examples, you can improve your financial literacy, enhance your problem-solving abilities, and gain a deeper understanding of numerical relationships. Whether you're calculating discounts, analyzing data, or simply trying to make sense of the numbers in your life, a solid grasp of percentages is an invaluable asset.
Now that you've mastered the basics, why not put your skills to the test? Try calculating percentages in different contexts, such as figuring out the tip at a restaurant or comparing the interest rates on different loans. Share your results and insights with friends and family, and encourage them to improve their percentage calculation skills as well. By working together, we can all become more confident and capable in our interactions with numbers.
Latest Posts
Latest Posts
-
Who Killed Sam Westing In The Westing Game
Nov 27, 2025
-
What Was The Setting Of To Kill A Mockingbird
Nov 27, 2025
-
Who Wrote The Book The Pearl
Nov 27, 2025
-
Weight Of 32 Ounces Of Water
Nov 27, 2025
-
How To Tell If A Graph Is Linear
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about 3 Of 15 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.