30 Is What Percent Of 15
sandbardeewhy
Nov 28, 2025 · 11 min read
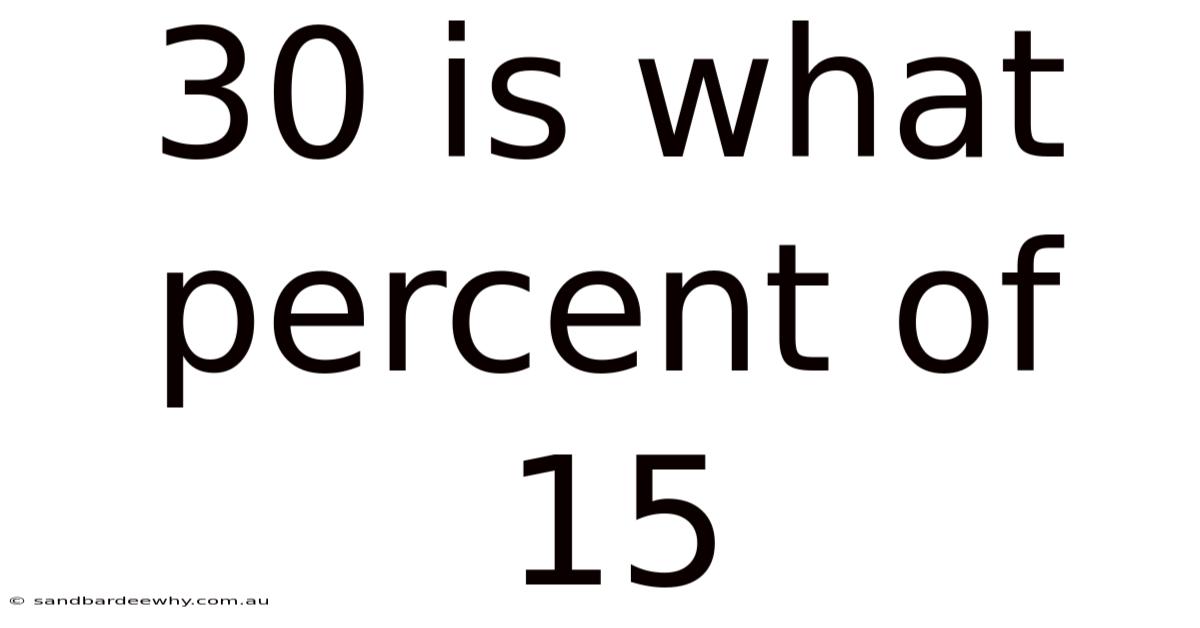
Table of Contents
Imagine you're at a farmers market, eyeing a beautiful basket of apples. The sign says "15 apples for $10," but you only want 30 apples. How much will that cost? This simple question boils down to understanding percentages and how they relate to proportions. Calculating "30 is what percent of 15" isn't just about math; it's a fundamental skill applicable in everyday scenarios, from shopping to understanding financial reports.
Think about a pizza cut into 15 slices. If you eat 30 slices, you've essentially consumed two whole pizzas. Translating this to percentages means you've eaten 200% of the original pizza (represented by the 15 slices). While seemingly simple, this example highlights the core concept: percentages allow us to express a part (or, in this case, more than the whole) in relation to a whole, making comparisons and analyses much easier. Let’s delve into the process of calculating this seemingly paradoxical percentage.
Understanding the Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Understanding percentages is crucial for various applications, including calculating discounts, interest rates, statistics, and much more. They provide a standardized way to compare proportions, making complex information more accessible and understandable.
Percentages are essentially ratios or fractions with a denominator of 100. When we say "50 percent," we mean 50 out of 100, often written as 50/100 or 0.50 in decimal form. This simple concept is the foundation for understanding more complex percentage calculations. It allows us to express parts of a whole in a consistent and easily comparable manner, which is why percentages are so widely used.
The concept of percentages can be traced back to ancient Rome, where calculations involving fractions with a denominator of 100 were common. However, the modern percentage symbol (%) didn't appear until much later. It gradually evolved from abbreviations like "per 100" or "P cento." The use of percentages became more standardized with the growth of commerce and finance, providing a practical way to calculate interest, taxes, and profits. Today, percentages are an indispensable tool in almost every field, from science and engineering to economics and marketing.
At its core, calculating "30 is what percent of 15" involves finding the ratio between the two numbers and then converting that ratio into a percentage. This process can be applied to any pair of numbers, making it a versatile tool for understanding proportions. Understanding the basic principles of percentages allows us to accurately interpret and use data in various contexts.
Mastering percentages requires understanding the relationship between fractions, decimals, and percentages. Each form represents the same proportion but in different ways. For example, 1/4 can be expressed as 0.25 or 25%. Being able to convert between these forms is crucial for solving percentage problems efficiently. This flexibility allows for easier calculations and comparisons, making the process more intuitive.
Step-by-Step Calculation: 30 is What Percent of 15?
Calculating "30 is what percent of 15" involves a simple formula that can be applied to similar percentage problems. Here’s a detailed breakdown:
-
Identify the Numbers: In this scenario, 30 is the part and 15 is the whole (or the base). We want to find out what percentage 30 represents of 15.
-
Set up the Ratio: To find the percentage, we first set up a ratio: Part / Whole = 30 / 15
-
Calculate the Ratio: Divide the part by the whole: 30 / 15 = 2
-
Convert to Percentage: Multiply the result by 100 to convert it into a percentage: 2 * 100 = 200%
So, 30 is 200% of 15. This means that 30 is twice as large as 15. The percentage can be greater than 100% when the part is larger than the whole. This result is perfectly valid and highlights the importance of understanding the context when interpreting percentages.
This calculation method can be universally applied to any percentage problem. By identifying the part and the whole and following the steps outlined above, you can accurately determine the percentage. Remember to always double-check your work, particularly when dealing with percentages greater than 100%, to ensure that the result makes sense in the given context.
Understanding the distinction between the part and the whole is essential for accurate percentage calculations. The whole represents the total amount or the base, while the part is a portion of that whole. In the case of "30 is what percent of 15," 15 is the base, and 30 is the quantity we are comparing to that base. This distinction guides the setup of the ratio and ensures correct calculations.
The key to mastering percentage calculations lies in consistent practice and a clear understanding of the underlying concepts. By working through various examples and applying the formula methodically, you can develop confidence and accuracy in solving percentage problems. This skill is invaluable in various real-world scenarios, from personal finance to professional analysis.
Real-World Applications of Percentage Calculations
Percentage calculations are incredibly versatile and find applications in numerous real-world scenarios. Whether you're calculating discounts at a store, understanding financial reports, or analyzing statistical data, percentages are an essential tool. Here are some common examples:
-
Retail Discounts: When a store advertises a "30% off" sale, you're using percentages to calculate the discounted price. For example, if an item originally costs $50, a 30% discount means you save $15 (30% of $50), and the final price is $35.
-
Financial Investments: Interest rates on savings accounts or loans are expressed as percentages. Understanding these rates helps you determine the amount of interest you'll earn or pay over time. For example, a 5% annual interest rate on a $1000 investment means you'll earn $50 in interest after one year.
-
Exam Scores: Test scores are often reported as percentages. If you get 75 out of 100 questions correct on a test, your score is 75%. This provides a standardized way to compare your performance against others.
-
Business Analysis: Businesses use percentages to analyze sales growth, profit margins, and market share. For example, if a company's sales increase from $1 million to $1.2 million, the sales growth is 20%.
-
Health and Nutrition: Nutritional information on food labels often includes percentages to indicate the proportion of daily recommended values. For example, a food item might contain 15% of the daily recommended intake of vitamin C.
-
Statistical Analysis: Percentages are used to present statistical data in an easily understandable format. For example, a survey might report that 60% of respondents prefer a particular product.
These examples demonstrate the wide range of applications for percentage calculations. By understanding how to work with percentages, you can make informed decisions in various aspects of life, from personal finance to professional analysis.
Common Mistakes and How to Avoid Them
While percentage calculations are straightforward, certain common mistakes can lead to incorrect results. Being aware of these pitfalls and knowing how to avoid them can significantly improve accuracy.
-
Confusing the Part and the Whole: One of the most frequent errors is misidentifying the part and the whole. Always clearly define which number represents the total amount and which represents the portion being compared. For instance, in the question "What percent of 50 is 20?", 50 is the whole, and 20 is the part.
-
Incorrectly Converting Decimals to Percentages: Remember to multiply the decimal by 100 to convert it into a percentage. For example, 0.25 should be multiplied by 100 to become 25%. Forgetting this step can lead to significant errors.
-
Misinterpreting Percentage Increase or Decrease: When calculating percentage increase or decrease, ensure you are using the correct base value. The formula is:
[(New Value - Old Value) / Old Value] * 100. Using the new value as the base will result in an incorrect percentage change. -
Forgetting to Convert Percentages to Decimals for Calculations: When performing calculations with percentages, it's essential to convert them back to decimals. For example, to calculate 20% of 50, convert 20% to 0.20 and then multiply by 50.
-
Assuming Percentages are Always Less Than 100%: As demonstrated earlier, percentages can be greater than 100% when the part is larger than the whole. Understanding this concept is crucial for accurate interpretation.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with long decimals. Round at the end of the calculation rather than in the middle to maintain accuracy.
By being aware of these common mistakes and taking steps to avoid them, you can ensure the accuracy of your percentage calculations. Double-checking your work and understanding the underlying concepts will also help prevent errors.
Tips for Mastering Percentage Calculations
Mastering percentage calculations involves more than just memorizing formulas; it requires a solid understanding of the underlying concepts and consistent practice. Here are some tips to help you improve your skills:
-
Understand the Basics: Ensure you have a strong grasp of the fundamental concepts of percentages, including the relationship between fractions, decimals, and percentages. This understanding forms the foundation for more complex calculations.
-
Practice Regularly: Consistent practice is key to mastering any mathematical skill. Work through various examples and exercises to reinforce your understanding and improve your speed and accuracy.
-
Use Real-World Examples: Apply percentage calculations to real-world scenarios, such as calculating discounts, understanding financial reports, or analyzing statistical data. This helps you see the practical applications of percentages and makes the learning process more engaging.
-
Break Down Complex Problems: When faced with a complex problem, break it down into smaller, more manageable steps. This makes the problem less daunting and easier to solve accurately.
-
Use Visual Aids: Visual aids, such as diagrams or charts, can help you visualize percentage problems and understand the relationships between different quantities.
-
Check Your Work: Always double-check your work to ensure accuracy. This helps you identify and correct any errors before they become a problem.
-
Seek Help When Needed: Don't hesitate to seek help from teachers, tutors, or online resources if you are struggling with percentage calculations. Understanding the concepts is crucial for long-term success.
-
Use Online Tools: There are many online calculators and resources available that can help you practice and check your percentage calculations. These tools can be valuable for reinforcing your understanding and improving your accuracy.
By following these tips and dedicating time to practice, you can master percentage calculations and confidently apply them in various aspects of your life.
FAQ on Percentage Calculations
Q: What does "percent" mean?
A: "Percent" comes from the Latin per centum, meaning "out of one hundred." It's a way of expressing a number as a fraction of 100.
Q: How do I convert a decimal to a percentage?
A: Multiply the decimal by 100. For example, 0.75 becomes 75%.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100% if the part is larger than the whole. For example, 30 is 200% of 15.
Q: How do I calculate a percentage increase?
A: Use the formula: [(New Value - Old Value) / Old Value] * 100.
Q: How do I calculate a percentage decrease?
A: Use the formula: [(Old Value - New Value) / Old Value] * 100.
Q: What's the difference between "percent of" and "percent off"?
A: "Percent of" is used to find a portion of a whole (e.g., 20% of 50). "Percent off" is used to calculate a discount (e.g., 20% off a $50 item).
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator, then multiply by 100. For example, 1/4 = 0.25, and 0.25 * 100 = 25%.
Q: What is the formula for finding what percentage one number is of another?
A: The formula is: (Part / Whole) * 100.
Conclusion
Understanding that "30 is what percent of 15" is more than just a mathematical exercise; it's a practical skill that enhances our ability to interpret and analyze information in everyday life. Whether it's calculating discounts, understanding financial reports, or analyzing statistical data, percentages provide a standardized and accessible way to compare proportions. By mastering the basic principles, avoiding common mistakes, and practicing regularly, anyone can become proficient in percentage calculations.
Remember, the key to success lies in understanding the underlying concepts and applying them consistently. Don't hesitate to revisit the formulas, practice with real-world examples, and seek help when needed. Confidently tackle percentage problems and unlock a valuable skill that will benefit you in various aspects of life. Now that you've grasped the core concepts, take the next step and apply your knowledge to real-world scenarios. Calculate that discount, analyze that report, and empower yourself with the power of percentages!
Latest Posts
Latest Posts
-
What Is Structure In A Poem
Nov 28, 2025
-
Examples Of A Norm Referenced Test
Nov 28, 2025
-
What Separates The Inner Planets From The Outer Planets
Nov 28, 2025
-
How To Determine Acid Or Base From Chemical Formula
Nov 28, 2025
-
Theme For Lord Of The Flies
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about 30 Is What Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.