30 Of What Number Is 15
sandbardeewhy
Nov 27, 2025 · 9 min read
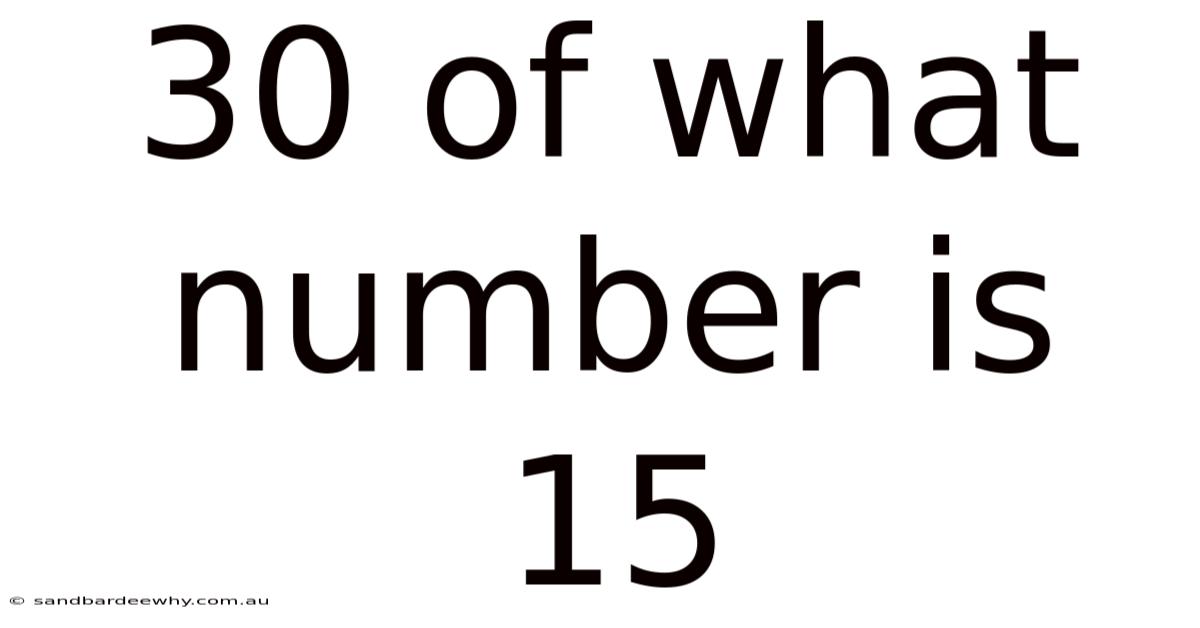
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a beautiful display of ripe, juicy peaches. The vendor tells you, "These peaches are 30% off, and you'll save $15!" Intrigued, you wonder, "What was the original price of these peaches before the discount?" Or perhaps you are managing a project budget. You know that $15 has been allocated for marketing, representing 30% of the total marketing budget. Now, you need to figure out what the full marketing budget is to plan the rest of your strategies. These scenarios highlight a common mathematical problem: figuring out "30% of what number is 15?"
This type of problem isn't just a classroom exercise; it's a practical skill that comes up in everyday life, from shopping and finance to project management and beyond. Understanding how to solve it efficiently can empower you to make informed decisions and navigate various real-world situations with confidence. In this comprehensive guide, we'll explore the ins and outs of tackling this question, providing you with a solid understanding of the underlying principles and practical techniques to find the answer quickly and accurately.
Unveiling the Mystery: 30% of What Number Equals 15?
To grasp the concept fully, let’s break down the core question: "30% of what number is 15?". Essentially, we're looking for a whole number, let’s call it 'x', where thirty percent of that number is equal to fifteen. This is a classic percentage problem, and solving it involves understanding the relationship between percentages, fractions, and decimals.
The Foundation: Understanding Percentages
At its core, a percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." So, 30% simply means 30 out of 100, or 30/100. This can be further simplified to the fraction 3/10 or expressed as the decimal 0.30. Understanding this conversion is crucial for solving percentage-related problems. It allows us to translate a percentage into a format that's easier to work with in equations and calculations. Whether you're calculating discounts, interest rates, or proportions, a firm grasp of percentages is essential.
Historical Roots of Percentages
The concept of percentages has a long and fascinating history, dating back to ancient Rome. The Romans often used fractions that were multiples of one hundred to calculate taxes, trade, and interest. However, the modern concept of percentages as we know it today began to take shape during the Renaissance. As trade and commerce flourished, there was an increasing need for standardized ways to calculate profits, losses, and interest rates. Mathematicians and merchants began to use percentages more widely, and the notation we use today (the "%" symbol) gradually evolved over time.
By the 17th century, percentages had become an integral part of financial calculations and were widely used in Europe. The adoption of the metric system further solidified the use of percentages, as it provided a consistent base for calculations. Today, percentages are used in virtually every field, from finance and economics to science and engineering. They provide a convenient and universally understood way to express proportions and changes, making complex information more accessible and understandable.
The Mathematical Approach: Setting Up the Equation
Now that we understand the basics of percentages, let's translate our problem into a mathematical equation. The statement "30% of what number is 15" can be written as:
30% * x = 15
To solve for 'x', we need to isolate it on one side of the equation. Since 30% is equivalent to 0.30, we can rewrite the equation as:
- 30 * x = 15
To isolate 'x', we divide both sides of the equation by 0.30:
x = 15 / 0.30
Performing the division, we find:
x = 50
Therefore, 30% of 50 is 15. This confirms that the original number we were looking for is 50. Whether you're calculating the original price of an item after a discount, determining the total budget based on a percentage allocation, or solving any other similar problem, this method provides a reliable way to find the answer.
Alternative Methods
While the algebraic approach is the most straightforward, there are alternative methods to solve this type of problem. One common method involves using proportions. We can set up a proportion as follows:
30 / 100 = 15 / x
Here, we're saying that 30 is to 100 as 15 is to 'x'. To solve for 'x', we can cross-multiply:
30 * x = 15 * 100 30x = 1500
Dividing both sides by 30:
x = 1500 / 30 x = 50
Another method involves using the concept of fractions. Since 30% is equal to 3/10, we can say that 3/10 of 'x' is 15. To find 'x', we can multiply 15 by the reciprocal of 3/10, which is 10/3:
x = 15 * (10/3) x = 150 / 3 x = 50
Each of these methods provides a slightly different way to approach the problem, but they all lead to the same answer: 50.
Emerging Trends and Modern Applications
In today's data-driven world, understanding percentages is more important than ever. From analyzing market trends to interpreting scientific data, percentages are used extensively to make sense of complex information. One significant trend is the increasing use of data visualization tools to represent percentages in a more intuitive way. Tools like Tableau, Power BI, and Google Data Studio allow users to create interactive charts and graphs that highlight key insights and trends. These visualizations make it easier for decision-makers to understand and act on the data.
Another trend is the use of machine learning algorithms to analyze large datasets and identify patterns and correlations that might not be immediately apparent. These algorithms often rely on percentages to quantify the strength of relationships between different variables. For example, in marketing, machine learning can be used to analyze customer data and identify the percentage of customers who are likely to respond to a particular campaign. This information can then be used to optimize marketing strategies and improve ROI.
Furthermore, with the rise of e-commerce, percentages are playing an increasingly important role in online sales and marketing. Online retailers use percentages to calculate discounts, promotions, and sales tax. They also use percentages to track key metrics such as conversion rates, bounce rates, and customer retention rates. Understanding these metrics is crucial for optimizing online sales and improving the customer experience.
Practical Tips and Expert Advice
Solving percentage problems can sometimes be tricky, but with the right approach, it can become much easier. Here are some practical tips and expert advice to help you tackle these problems with confidence:
-
Understand the Language: Pay close attention to the wording of the problem. Key words like "of," "is," and "what" can provide valuable clues about how to set up the equation. For example, "of" usually indicates multiplication, "is" indicates equality, and "what" indicates the unknown variable.
-
Convert Percentages to Decimals: Whenever possible, convert percentages to decimals before performing calculations. This will simplify the math and reduce the risk of errors. To convert a percentage to a decimal, divide it by 100. For example, 30% becomes 0.30.
-
Use Proportions: Proportions can be a powerful tool for solving percentage problems, especially when you're dealing with ratios or comparing two different quantities. Set up the proportion carefully, making sure to align the corresponding values.
-
Check Your Answer: After solving the problem, always check your answer to make sure it makes sense in the context of the problem. For example, if you're calculating a discount, make sure the discounted price is lower than the original price.
-
Practice Regularly: Like any mathematical skill, solving percentage problems requires practice. Work through a variety of problems to build your confidence and improve your problem-solving skills.
-
Use Technology: Take advantage of technology to simplify your calculations. Calculators, spreadsheets, and online tools can help you quickly and accurately solve percentage problems.
-
Real-World Examples: Apply your knowledge to real-world scenarios. Whether you're calculating discounts while shopping or figuring out how much to tip at a restaurant, practicing in everyday situations will reinforce your understanding of percentages.
-
Seek Help When Needed: Don't hesitate to ask for help if you're struggling with a particular problem. Consult with a teacher, tutor, or online resource to get clarification and guidance.
FAQ: Addressing Common Questions
Q: How do I convert a percentage to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 30% is equal to 30/100, which simplifies to 3/10.
Q: How do I find the percentage of a number?
A: To find the percentage of a number, multiply the number by the percentage expressed as a decimal. For example, to find 30% of 50, multiply 50 by 0.30, which equals 15.
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase is the amount by which a number has increased, expressed as a percentage of the original number. Percentage decrease is the amount by which a number has decreased, expressed as a percentage of the original number. The formulas for calculating percentage increase and decrease are:
- Percentage Increase = ((New Value - Original Value) / Original Value) * 100
- Percentage Decrease = ((Original Value - New Value) / Original Value) * 100
Q: How do I calculate a percentage change?
A: To calculate a percentage change, use the following formula:
Percentage Change = ((New Value - Original Value) / Original Value) * 100
If the result is positive, it represents a percentage increase. If the result is negative, it represents a percentage decrease.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when you're comparing a new value to an original value and the new value is more than twice the original value. For example, if a company's revenue doubles from $100,000 to $200,000, the percentage increase is 100%. If the revenue triples to $300,000, the percentage increase is 200%.
Conclusion: Mastering the Art of Percentage Calculations
In conclusion, understanding how to solve "30% of what number is 15" is more than just a mathematical exercise; it's a practical skill that can empower you to make informed decisions in various real-life situations. By grasping the underlying principles of percentages, mastering the algebraic approach, and exploring alternative methods, you can confidently tackle a wide range of percentage-related problems. Remember to pay attention to the language of the problem, convert percentages to decimals, use proportions when appropriate, and always check your answer. With practice and the right approach, you can master the art of percentage calculations and apply your knowledge to solve real-world problems with ease.
Now that you've gained a solid understanding of how to solve this type of problem, why not test your knowledge with some practice questions? Share your answers in the comments below and let us know if you have any questions or insights to share. Your engagement will not only reinforce your own learning but also help others who are on the same journey to master the art of percentage calculations.
Latest Posts
Latest Posts
-
What Is A Rule For Subtracting Integers
Nov 27, 2025
-
Why The International Date Line Is Not Straight
Nov 27, 2025
-
6 2 3 As An Improper Fraction
Nov 27, 2025
-
Is A Quart Half A Gallon
Nov 27, 2025
-
How Long Does A Llama Live
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about 30 Of What Number Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.