36 Of 50 Is What Percentage
sandbardeewhy
Nov 21, 2025 · 10 min read
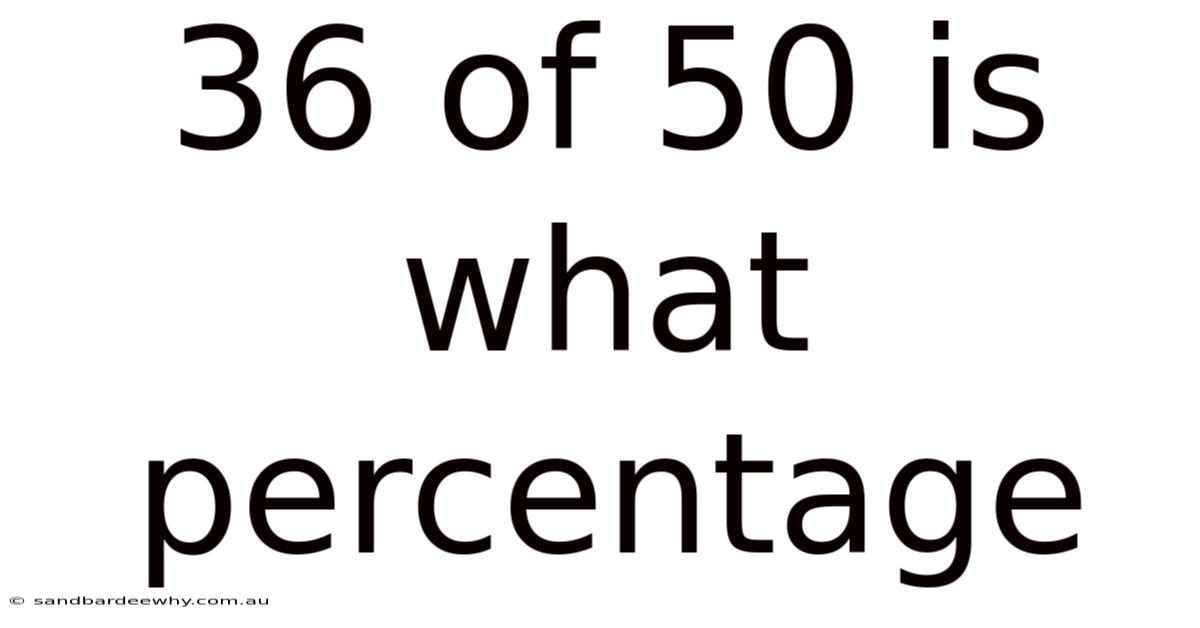
Table of Contents
Imagine you're at a school fair, playing a ring toss game. There are 50 bottles, and you manage to land rings on 36 of them. Someone asks, "Hey, what percentage of the bottles did you get?" Or perhaps you're tracking your progress on a fitness challenge: out of 50 planned workouts, you've completed 36. You might wonder, "What percentage of my goal have I achieved?"
These scenarios highlight a common need: figuring out what percentage one number represents of another. In this case, we want to know "36 of 50 is what percentage?" Understanding how to calculate percentages is a fundamental skill that applies to various aspects of daily life, from calculating discounts at the store to understanding statistics in the news. This article will provide a comprehensive guide to understanding and calculating percentages, using "36 of 50" as a key example. We will explore the underlying principles, practical applications, current trends, expert tips, and frequently asked questions to give you a complete grasp of this essential mathematical concept.
Main Subheading
At its core, the question "36 of 50 is what percentage?" is about expressing a fraction as a percentage. Percentages are a standardized way of representing proportions, making it easy to compare different fractions and understand their relative sizes. The concept of percentage is deeply rooted in history and has become an indispensable tool in fields ranging from finance to science.
Understanding percentages is not just a mathematical exercise; it’s a practical skill that empowers you to make informed decisions. Whether you're calculating tips at a restaurant, understanding interest rates on a loan, or analyzing sales data at work, percentages provide a clear and concise way to understand and compare quantities. The ability to quickly and accurately calculate percentages can significantly enhance your numerical literacy and decision-making capabilities.
Comprehensive Overview
The word "percent" comes from the Latin per centum, meaning "out of one hundred." Thus, a percentage is a way of expressing a number as a fraction of 100. This standardization allows for easy comparison of different ratios. For example, saying that 36 out of 50 is 72% immediately gives you a sense of the proportion, which might not be as clear if you only knew the fraction 36/50.
To understand the mathematical foundation, consider the basic formula for calculating a percentage:
Percentage = (Part / Whole) * 100
In the context of our question, "36 of 50 is what percentage?", 36 is the part, and 50 is the whole. Plugging these values into the formula gives us:
Percentage = (36 / 50) * 100
Calculating this, we get:
Percentage = 0.72 * 100 = 72%
So, 36 of 50 is 72%. This means that 36 is 72% of 50.
The history of percentages dates back to ancient Rome, where calculations were often made in terms of fractions of 100. However, the modern concept of percentage as we know it gained prominence during the Renaissance, with the growth of commerce and the need for standardized ways to calculate interest, taxes, and profits. The use of the percent sign (%) became widespread in the 17th century, further solidifying the importance of percentages in mathematics and finance.
Percentages are fundamental in various fields:
- Finance: Interest rates, investment returns, and profit margins are all expressed as percentages. Understanding these figures is crucial for making sound financial decisions.
- Statistics: Percentages are used to present data in a clear and understandable format. For instance, survey results and demographic information are often expressed as percentages.
- Retail: Discounts, sales tax, and markups are calculated using percentages. Knowing how to calculate these values helps consumers and businesses alike.
- Science: Concentrations of solutions, error margins in experiments, and growth rates are often expressed as percentages.
- Education: Grades and test scores are frequently represented as percentages, providing a standardized measure of performance.
Understanding how to convert between fractions, decimals, and percentages is crucial. A fraction can be converted to a decimal by dividing the numerator by the denominator. To convert a decimal to a percentage, multiply by 100. Conversely, to convert a percentage to a decimal, divide by 100. For example:
- Fraction to Decimal: 36/50 = 0.72
- Decimal to Percentage: 0.72 * 100 = 72%
- Percentage to Decimal: 72% / 100 = 0.72
Trends and Latest Developments
In recent years, the use of percentages has evolved with the increasing reliance on data analytics and visualization. Data scientists and analysts use percentages to communicate complex information in a simplified manner. This is particularly evident in fields like marketing, where understanding conversion rates (the percentage of visitors who complete a desired action) is critical for optimizing campaigns.
Another trend is the growing emphasis on data literacy, which includes the ability to understand and interpret percentages accurately. Misinterpreting percentages can lead to flawed decision-making, so educational initiatives are focusing on improving numerical skills. This is especially important in an era of fake news and misinformation, where statistics are often manipulated or misrepresented.
According to recent surveys, a significant percentage of adults struggle with basic percentage calculations. This highlights the need for continued education and awareness. Many online tools and apps have been developed to assist with percentage calculations, making it easier for people to perform these tasks quickly and accurately. These tools often include features like percentage calculators, discount calculators, and tip calculators, which cater to everyday needs.
From a professional perspective, understanding how to use percentages in presentations and reports is highly valued. Visual aids like charts and graphs often use percentages to illustrate trends and patterns. Being able to present data in a clear and compelling way is a key skill in many industries.
Tips and Expert Advice
Calculating percentages accurately and efficiently requires some practice and a few helpful tips. Here are some expert-backed strategies to enhance your skills:
-
Understand the Base: Always identify the whole or the base number that you are calculating the percentage from. In the example "36 of 50 is what percentage?", the base is 50. Misidentifying the base can lead to incorrect calculations. For instance, if you were calculating a discount on a product, the original price would be the base.
To further illustrate this point, consider a scenario where you're tracking sales growth. If your sales increased from $100 to $120, the base is $100, and the increase is $20. The percentage increase would be ($20 / $100) * 100 = 20%. Understanding that the initial sales figure is the base ensures an accurate calculation of growth.
-
Convert to Decimal First: Converting the fraction to a decimal before multiplying by 100 can simplify the calculation. This is particularly useful when dealing with more complex fractions. In our example, 36/50 = 0.72, and then multiplying by 100 gives 72%.
Using decimals also makes it easier to compare different percentages. For example, if you want to compare 36/50 (0.72) with 40/60 (approximately 0.67), the decimal form allows for a quick comparison. This is especially helpful when analyzing data sets with multiple percentages.
-
Use Benchmarks: Familiarize yourself with common percentage benchmarks like 25%, 50%, and 75%. Knowing that 50% is half and 25% is a quarter can help you quickly estimate percentages and check the reasonableness of your calculations.
For instance, if you're calculating 25% of 50, you can quickly determine that it should be around 12.5 (since 50/4 = 12.5). This mental estimation helps you catch any significant errors in your calculations.
-
Practice Regularly: The more you practice calculating percentages, the more comfortable and confident you will become. Try incorporating percentage calculations into your daily life, such as calculating discounts while shopping or estimating tips at restaurants.
Regular practice helps reinforce the underlying concepts and improves your speed and accuracy. You can also use online quizzes and exercises to test your skills and identify areas where you need more practice.
-
Utilize Technology: Take advantage of calculators and online tools to verify your calculations. These tools can help you avoid errors and save time. However, it's still important to understand the underlying principles so that you can interpret the results correctly.
Many spreadsheet programs like Microsoft Excel and Google Sheets have built-in functions for calculating percentages. Learning to use these tools can significantly enhance your productivity and accuracy in professional settings.
-
Double-Check Your Work: Always double-check your calculations, especially when dealing with important financial or statistical data. A small error in a percentage calculation can have significant consequences.
One effective strategy is to use a different method to verify your results. For example, if you calculated a percentage using the formula (Part / Whole) * 100, you can check your answer by working backward to see if the percentage you calculated yields the original part.
-
Understand Common Mistakes: Be aware of common errors, such as confusing the part and the whole, or forgetting to multiply by 100. Recognizing these pitfalls can help you avoid them.
Another common mistake is misinterpreting percentage increases and decreases. For example, a 50% decrease followed by a 50% increase does not return the original value. It's essential to understand that percentage changes are relative to the current value, not the original value.
FAQ
Q: What is the formula for calculating percentage?
A: The formula is: Percentage = (Part / Whole) * 100.
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator to get a decimal, then multiply by 100. For example, to convert 36/50 to a percentage, calculate (36 / 50) * 100 = 72%.
Q: How do I convert a percentage to a decimal?
A: Divide the percentage by 100. For example, 72% as a decimal is 72 / 100 = 0.72.
Q: What is the difference between percentage and percentile?
A: Percentage expresses a part of a whole in terms of 100, while percentile indicates the value below which a given percentage of observations in a group of observations fall.
Q: How can I calculate a percentage increase or decrease?
A: For a percentage increase: ((New Value - Old Value) / Old Value) * 100. For a percentage decrease: ((Old Value - New Value) / Old Value) * 100.
Q: Why are percentages important?
A: Percentages provide a standardized way to compare proportions, making it easier to understand and interpret data in various fields such as finance, statistics, retail, and science.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include confusing the part and the whole, forgetting to multiply by 100, and misinterpreting percentage increases and decreases.
Conclusion
In summary, understanding how to calculate percentages, such as determining that "36 of 50 is 72%," is a fundamental skill with wide-ranging applications. Percentages allow us to express proportions in a standardized and easily understandable way, making them essential tools in finance, statistics, retail, and everyday decision-making. By mastering the basic formula, understanding the underlying principles, and practicing regularly, you can enhance your numerical literacy and make more informed decisions.
Now that you have a comprehensive understanding of percentages, put your knowledge to the test! Calculate percentages in your daily life, whether it's figuring out discounts while shopping or tracking your progress towards a goal. Share your experiences and any tips you've found helpful in the comments below. Let's continue the conversation and help each other become more proficient with percentages. If you found this article helpful, share it with your friends and colleagues to spread the knowledge!
Latest Posts
Latest Posts
-
What Is The Highest Asvab Score You Can Get
Nov 21, 2025
-
1 3 Divided By 2 In Fraction
Nov 21, 2025
-
Is A Parallelogram Always A Square
Nov 21, 2025
-
How Many Cups Are In 1 2 Gallon Of Milk
Nov 21, 2025
-
How To Know If An Equation Is A Function
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 36 Of 50 Is What Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.