4 Is What Percent Of 20
sandbardeewhy
Nov 23, 2025 · 14 min read
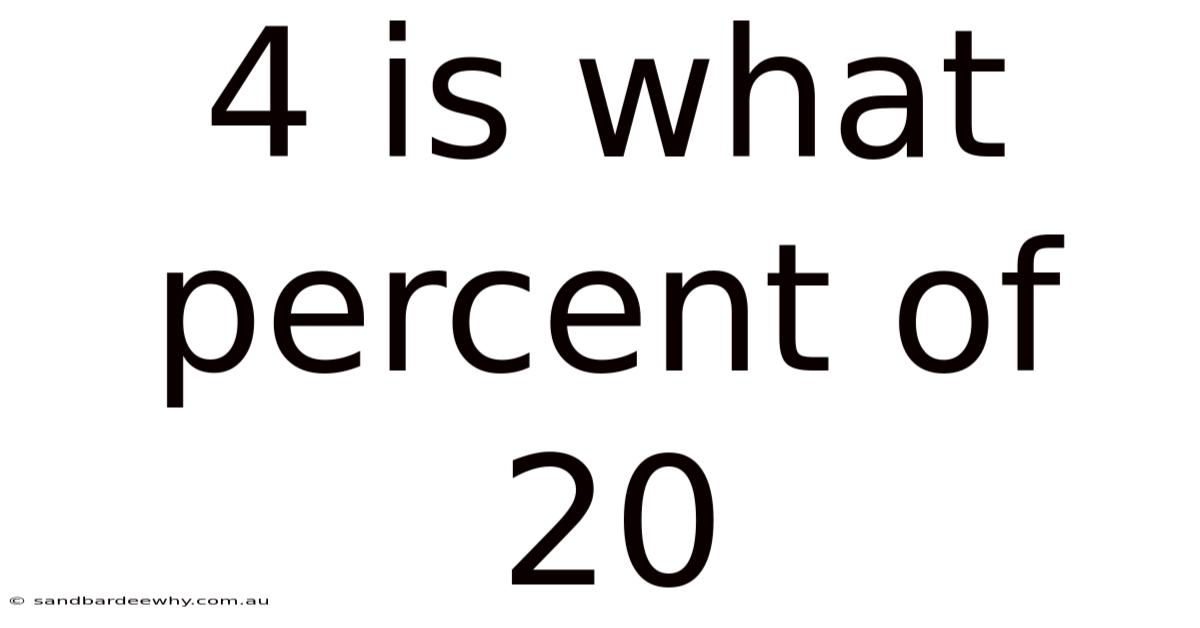
Table of Contents
Have you ever found yourself in a situation where you needed to calculate percentages quickly? Perhaps you were splitting a bill with friends, figuring out a discount at the store, or maybe even trying to understand some financial data. Percentages are all around us, and understanding how to calculate them is a fundamental skill. Let’s consider a scenario: you’re at a coffee shop, and your total bill comes to $20. You have a $4 coupon. What percentage discount does that coupon represent? This is where the ability to calculate "4 is what percent of 20" comes into play.
Simple percentage problems like this are more than just mathematical exercises; they are practical tools for everyday life. Whether you are a student trying to grasp basic math concepts, a professional needing to analyze data, or just someone managing personal finances, understanding percentages can empower you to make informed decisions. This article will delve into the straightforward calculation of finding what percentage one number is of another, using "4 is what percent of 20" as our main example. We’ll break down the concepts, explore different methods, look at real-world applications, and provide you with expert tips to master percentage calculations.
Main Subheading: Understanding the Basics of Percentage Calculation
Percentages are a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Essentially, a percentage tells us how many parts out of 100 we have. This concept is crucial in many areas, from finance and economics to everyday situations like shopping and cooking.
To truly understand what it means to ask, "4 is what percent of 20," we need to break down the question into its components. In this context, 4 is the part, 20 is the whole, and we are trying to find the percentage. The basic formula to calculate this is:
Percentage = (Part / Whole) * 100
In our case:
- Part = 4
- Whole = 20
So, the formula becomes:
Percentage = (4 / 20) * 100
This formula essentially converts the fraction (4/20) into a percentage by multiplying it by 100. This gives us the equivalent value out of 100, which is what a percentage represents.
Comprehensive Overview of Percentages
Delving deeper into the concept of percentages requires understanding its historical roots, mathematical foundations, and practical applications. Percentages are not just abstract numbers; they are a fundamental tool for comparing quantities, understanding proportions, and making informed decisions.
Historical Context: The use of percentages can be traced back to ancient Rome, where calculations were often made in terms of fractions of 100. However, the modern concept of percentages became more formalized during the Renaissance, as trade and commerce expanded. The need for standardized ways of calculating interest, taxes, and profits led to the widespread adoption of percentages as a common mathematical tool.
Mathematical Foundation: At its core, a percentage is a ratio or fraction expressed as a part of 100. The symbol "%" is used to denote percentage. Mathematically, any number can be converted into a percentage by multiplying it by 100. For instance, the decimal 0.25 is equivalent to 25%. This conversion allows for easy comparison of different fractions or ratios. For example, comparing 1/4 and 1/5 directly might be less intuitive than comparing their percentage equivalents (25% and 20%, respectively).
Different Ways to Calculate Percentages:
-
Direct Calculation: This is the most straightforward method. Using the formula
Percentage = (Part / Whole) * 100, you can directly compute the percentage. For example, to find what percentage 30 is of 150:Percentage = (30 / 150) * 100 = 20% -
Using Decimals: Convert the fraction to a decimal first and then multiply by 100. This method is particularly useful when using a calculator. For example, to find what percentage 15 is of 75:
Decimal = 15 / 75 = 0.2Percentage = 0.2 * 100 = 20% -
Using Proportions: Set up a proportion to solve for the percentage. This method involves creating an equation where the ratios are equal. For example, to find what percentage 8 is of 40:
8 / 40 = x / 100Solving for x:x = (8 * 100) / 40 = 20%
Real-World Applications: Percentages are ubiquitous in daily life. Here are a few examples:
- Finance: Interest rates on loans and savings accounts are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
- Retail: Discounts and sales are often advertised as percentages. Knowing how to calculate these discounts can help you save money.
- Statistics: Percentages are used to represent data in a way that is easy to understand. For example, election results are often presented as percentages of the total vote.
- Health: Body fat percentage is a common measure of health. Understanding this percentage can help individuals track their fitness progress.
Common Mistakes to Avoid:
- Incorrectly Identifying the Part and Whole: Make sure you correctly identify which number is the part and which is the whole. Reversing them will lead to an incorrect percentage.
- Forgetting to Multiply by 100: After dividing the part by the whole, you must multiply by 100 to convert the decimal to a percentage.
- Misinterpreting the Result: Always consider the context of the percentage. A small percentage can be significant in some situations, while a large percentage might be negligible in others.
By understanding the historical context, mathematical foundation, various calculation methods, and real-world applications of percentages, you can gain a deeper appreciation for their importance and utility. Avoiding common mistakes will ensure that your percentage calculations are accurate and meaningful.
Trends and Latest Developments in Percentage Usage
While the fundamental concept of percentages remains constant, its application and relevance continue to evolve with modern trends and technological advancements. Understanding these trends and developments can provide valuable insights into how percentages are used in contemporary society and various industries.
Data Analysis and Visualization: In the era of big data, percentages are a crucial tool for simplifying and interpreting complex datasets. Data analysts use percentages to summarize findings, identify trends, and make comparisons. Visualizations such as pie charts, bar graphs, and dashboards often rely on percentages to present information in an accessible format. For example, market research reports frequently use percentages to show market share, customer satisfaction rates, and demographic breakdowns. The trend towards data-driven decision-making has amplified the importance of accurately calculating and interpreting percentages.
E-commerce and Online Marketing: E-commerce platforms and online marketers heavily rely on percentages to track performance, optimize campaigns, and drive sales. Conversion rates, click-through rates, and bounce rates are all expressed as percentages, providing valuable insights into user behavior and marketing effectiveness. For instance, an e-commerce site might analyze the percentage of visitors who add items to their cart versus those who complete a purchase to identify areas for improvement in the checkout process. A/B testing often involves comparing the percentage change in key metrics to determine which version of a webpage or advertisement performs better.
Financial Technology (FinTech): The FinTech industry has embraced percentages for a wide range of applications, from personal finance management to investment analysis. Robo-advisors use algorithms to allocate assets based on risk tolerance, often expressed as a percentage of the portfolio. Cryptocurrency platforms calculate transaction fees and returns as percentages. Budgeting apps help users track their spending by categorizing expenses and displaying them as percentages of their total income. The increasing accessibility of financial tools and data has empowered individuals to make more informed decisions using percentage-based metrics.
Education and Online Learning: Online learning platforms use percentages to track student progress, assess performance, and provide feedback. Completion rates, quiz scores, and assignment grades are often expressed as percentages, giving students a clear understanding of their performance relative to the course objectives. Adaptive learning technologies use percentage-based metrics to personalize the learning experience, adjusting the difficulty level and content based on the student's demonstrated mastery. This trend towards personalized learning is driving the need for accurate and meaningful percentage-based assessments.
Social and Political Polling: Public opinion polls and surveys use percentages to represent the distribution of responses and measure public sentiment. Approval ratings, voting intentions, and policy preferences are commonly expressed as percentages, providing insights into the attitudes and beliefs of the population. Political analysts use these percentages to forecast election outcomes, assess the impact of political events, and inform policy debates. The accuracy and reliability of these polls depend on the careful calculation and interpretation of percentages.
Professional Insights:
- Context Matters: Always consider the context when interpreting percentages. A small percentage change can be significant in some situations, while a large percentage change might be negligible in others.
- Base Size: Be mindful of the base size when comparing percentages. A 10% increase from a small base can be less meaningful than a 5% increase from a large base.
- Avoid Misleading Visualizations: Ensure that visualizations accurately represent the data and avoid distorting the percentages.
- Use Technology Wisely: Leverage technology tools and software to automate percentage calculations and reduce the risk of errors.
By staying informed about these trends and developments, you can enhance your ability to use percentages effectively in a variety of professional and personal contexts. Understanding the latest applications of percentages will empower you to make more informed decisions and communicate data more effectively.
Tips and Expert Advice for Mastering Percentage Calculations
Mastering percentage calculations involves more than just memorizing formulas. It requires a deep understanding of the underlying concepts and the ability to apply them in various real-world scenarios. Here are some tips and expert advice to help you become proficient in percentage calculations:
-
Understand the Language of Percentages: Familiarize yourself with the terminology used in percentage problems. Key terms include:
- Base: The total amount or whole.
- Rate: The percentage.
- Percentage: The part of the base that is calculated.
- Of: Indicates multiplication.
- Is: Indicates equality.
Understanding these terms will help you translate word problems into mathematical equations. For example, the statement "15 is 25% of 60" can be written as:
15 = 0.25 * 60 -
Practice Mental Math: Developing your mental math skills can significantly improve your ability to estimate and calculate percentages quickly. Here are some techniques to try:
- 10% Rule: To find 10% of a number, simply move the decimal point one place to the left. For example, 10% of 120 is 12.
- 5% Rule: To find 5% of a number, calculate 10% and then divide by 2. For example, 5% of 120 is 12 / 2 = 6.
- 1% Rule: To find 1% of a number, move the decimal point two places to the left. For example, 1% of 120 is 1.2.
Using these rules, you can quickly calculate other percentages. For example, to find 15% of 120, calculate 10% (12) + 5% (6) = 18.
-
Use Benchmarks: Benchmarks are common percentages that you should memorize to help you estimate and calculate more complex percentages. Some useful benchmarks include:
- 50% = 1/2
- 25% = 1/4
- 75% = 3/4
- 20% = 1/5
- 10% = 1/10
For example, if you need to find 48% of 200, you can estimate it as slightly less than 50%, which is 100.
-
Break Down Complex Problems: When faced with a complex percentage problem, break it down into smaller, more manageable steps. For example, to calculate a 15% discount on an item that costs $80, you can:
- Calculate 10% of $80: $8
- Calculate 5% of $80: $4 (half of 10%)
- Add the two amounts: $8 + $4 = $12
- Subtract the discount from the original price: $80 - $12 = $68
By breaking down the problem, you can reduce the risk of making errors and simplify the calculation process.
-
Check Your Work: Always double-check your work to ensure that your answer is reasonable and accurate. Use estimation techniques to approximate the answer and compare it to your calculated result. For example, if you calculate that 6 is 80% of 10, you should recognize that this is incorrect because 6 is clearly less than 80% of 10.
-
Apply Percentages in Real-Life Scenarios: The best way to master percentage calculations is to apply them in real-life scenarios. Look for opportunities to calculate discounts, tips, taxes, and other percentage-based quantities. The more you practice, the more comfortable and confident you will become.
Expert Advice:
- Use Technology as a Tool: While mental math is valuable, don't hesitate to use calculators and software to automate complex percentage calculations. These tools can help you save time and reduce the risk of errors.
- Understand the Context: Always consider the context of the percentage. A 5% increase in sales might be significant for a small business, but negligible for a large corporation.
- Communicate Clearly: When presenting percentage-based data, communicate clearly and concisely. Use visuals such as charts and graphs to help your audience understand the information.
By following these tips and expert advice, you can master percentage calculations and use them effectively in a variety of personal and professional contexts. Remember that practice is key, so look for opportunities to apply your knowledge and skills in everyday situations.
FAQ About Percentage Calculations
Q: What is the formula for calculating percentage?
A: The basic formula for calculating percentage is: Percentage = (Part / Whole) * 100. This formula tells you what percentage the "part" is of the "whole."
Q: How do I find the whole if I know the percentage and the part?
A: If you know the percentage and the part, you can find the whole using the formula: Whole = Part / (Percentage / 100). For example, if 20 is 25% of a number, the whole is 20 / (25 / 100) = 80.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100. For example, to convert 3/4 to a percentage: (3 / 4) * 100 = 75%.
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, to convert 0.65 to a percentage: 0.65 * 100 = 65%.
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase is the percentage by which a quantity has increased. It is calculated as: ((New Value - Original Value) / Original Value) * 100. Percentage decrease is the percentage by which a quantity has decreased. It is calculated as: ((Original Value - New Value) / Original Value) * 100.
Q: How do I calculate percentage change?
A: Percentage change is calculated using the formula: ((New Value - Original Value) / Original Value) * 100. If the result is positive, it is a percentage increase. If the result is negative, it is a percentage decrease.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when the new value is more than double the original value. For example, if a quantity increases from 100 to 250, the percentage increase is ((250 - 100) / 100) * 100 = 150%.
Q: How do I calculate a discount using percentages? A: To calculate a discount using percentages, multiply the original price by the discount percentage (expressed as a decimal) and then subtract the result from the original price. For example, if an item costs $50 and there is a 20% discount:
- Discount amount:
$50 * 0.20 = $10 - Final price:
$50 - $10 = $40
Q: How do I calculate a tip using percentages? A: To calculate a tip using percentages, multiply the bill amount by the tip percentage (expressed as a decimal). For example, if the bill is $30 and you want to leave a 15% tip:
- Tip amount:
$30 * 0.15 = $4.50
Q: What are some common mistakes to avoid when calculating percentages? A: Some common mistakes include:
- Incorrectly identifying the part and whole.
- Forgetting to multiply by 100.
- Misinterpreting the context of the percentage.
- Rounding prematurely, which can lead to inaccuracies.
Conclusion
In summary, understanding how to calculate percentages is an essential skill that can be applied in numerous real-life scenarios. From figuring out discounts at the store to understanding financial data, percentages help us make informed decisions and understand proportions. Calculating "4 is what percent of 20" is a straightforward application of the basic percentage formula, yielding 20%. By mastering the fundamentals, practicing regularly, and avoiding common mistakes, you can become proficient in percentage calculations.
Now that you have a comprehensive understanding of percentages, it's time to put your knowledge to the test. Try solving percentage problems in your daily life, whether it's calculating a tip at a restaurant or figuring out the sale price of an item. Share your experiences and any additional tips you have in the comments below! Let's help each other master the art of percentage calculation.
Latest Posts
Latest Posts
-
Difference Between A Wasp And A Hornet
Nov 23, 2025
-
Write The Quadratic Equation Whose Roots Are
Nov 23, 2025
-
Unit For Volume In Metric System
Nov 23, 2025
-
How Many Feet Is 90 Meters
Nov 23, 2025
-
How Do You Say I Will In Spanish
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about 4 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.