5 Out Of 20 As A Percentage
sandbardeewhy
Nov 25, 2025 · 10 min read
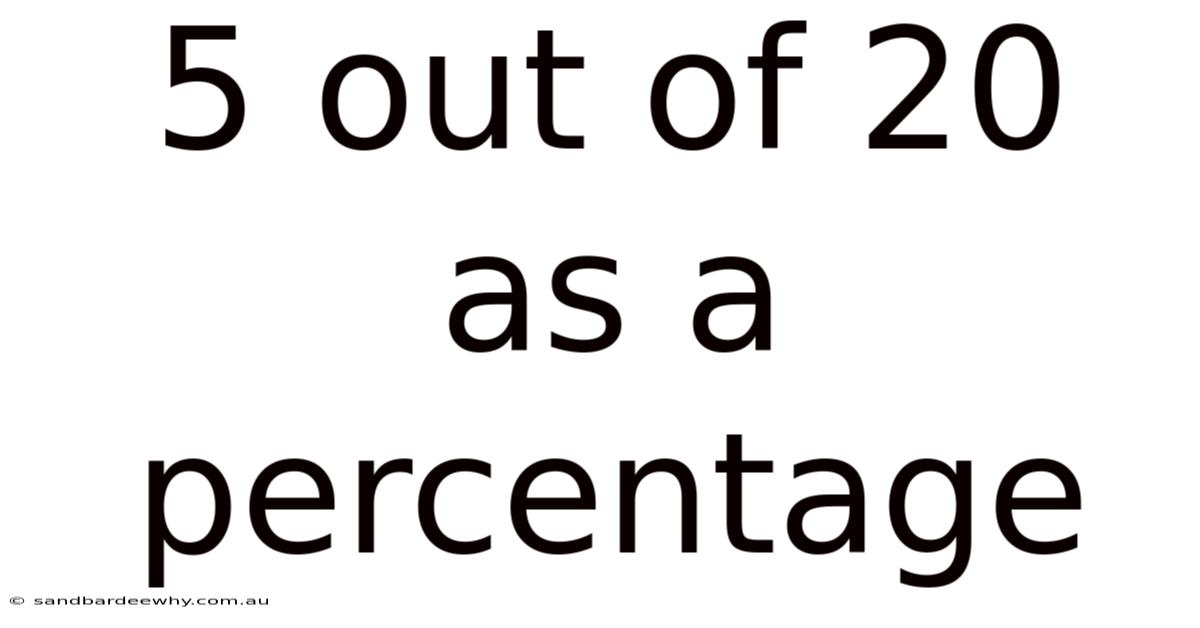
Table of Contents
The aroma of freshly brewed coffee fills the air as you sit at your desk, a stack of papers looming. Each sheet is marked with fractions, decimals, and percentages - remnants of a late-night study session. You're trying to master the art of converting numbers, a skill that feels both essential and elusive. Suddenly, a simple question pops into your head: What exactly is 5 out of 20 as a percentage? It seems straightforward, yet you hesitate, unsure if you truly grasp the fundamental concept.
The world is awash in numbers. From calculating discounts at your favorite store to understanding statistics in a research paper, percentages are ubiquitous. Knowing how to convert fractions into percentages, like figuring out what 5 out of 20 is as a percentage, is more than just an academic exercise. It's a practical skill that empowers you to make informed decisions every day. This article will break down the process step-by-step, offering insights and techniques that will demystify percentages and equip you with the confidence to tackle any numerical challenge.
Main Subheading: Understanding the Basics of Percentages
Percentages are a fundamental part of mathematics and everyday life, representing a proportion or ratio as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." This simple concept forms the basis for understanding many aspects of finance, statistics, and even everyday activities like shopping and cooking. Percentages provide a standardized way to compare different quantities, making it easier to grasp relative sizes and changes.
To truly appreciate percentages, it's important to understand their relationship with fractions and decimals. A percentage is essentially a fraction with a denominator of 100. For example, 50% is equivalent to 50/100, which simplifies to 1/2. Similarly, percentages can be easily converted into decimals by dividing by 100. So, 50% becomes 0.50. These conversions are crucial for performing calculations and understanding the meaning behind percentage values.
Comprehensive Overview: Diving Deep into Percentages
At its core, a percentage expresses a part of a whole as a number out of 100. This makes it an incredibly useful tool for standardizing comparisons. Imagine you are comparing the success rates of two marketing campaigns. One campaign resulted in 50 sales out of 200 leads, while the other generated 75 sales out of 300 leads. At first glance, it might seem like the second campaign was more successful. However, by converting these figures into percentages, you can see that the first campaign had a success rate of 25% (50/200 = 0.25 = 25%), while the second campaign had a success rate of also 25% (75/300 = 0.25 = 25%). The percentages reveal that both campaigns performed equally well in terms of converting leads into sales.
The concept of percentages dates back to ancient Rome, where calculations were often done in terms of fractions of 100. However, the modern percentage symbol (%) didn't appear until much later. It gradually evolved from a shorthand notation used in medieval manuscripts. Over time, the use of percentages became increasingly widespread, particularly in commerce and finance. Today, percentages are an indispensable part of nearly every industry, from banking and retail to healthcare and education.
Understanding the mathematical foundation of percentages is essential for mastering their application. The basic formula for calculating a percentage is:
(Part / Whole) * 100 = Percentage
In this formula, the "part" represents the specific quantity you are interested in, while the "whole" represents the total or reference value. Multiplying the resulting fraction by 100 converts it into a percentage. For example, if you want to find what percentage 15 is of 50, you would divide 15 by 50 (15/50 = 0.3) and then multiply by 100 (0.3 * 100 = 30%). Therefore, 15 is 30% of 50.
One common mistake people make when working with percentages is confusing the "part" and the "whole." Always make sure you understand which value represents the total and which value represents the specific portion you are interested in. Another common error is forgetting to multiply by 100. Remember that percentages are always expressed as a number out of 100, so this final step is crucial for obtaining the correct result.
Percentages are also used to calculate percentage increase and decrease, which are useful for tracking changes over time. To calculate percentage increase, you use the formula:
((New Value - Original Value) / Original Value) * 100 = Percentage Increase
For example, if a company's revenue increased from $100,000 to $120,000, the percentage increase would be ((120,000 - 100,000) / 100,000) * 100 = 20%. Similarly, to calculate percentage decrease, you use the formula:
((Original Value - New Value) / Original Value) * 100 = Percentage Decrease
If a product's price decreased from $50 to $40, the percentage decrease would be ((50 - 40) / 50) * 100 = 20%.
Trends and Latest Developments
In today's data-driven world, understanding and interpreting percentages is more important than ever. One notable trend is the increasing use of percentages in data visualization. Charts and graphs often use percentages to represent proportions and distributions, making complex data more accessible and understandable. For example, pie charts commonly use percentages to show the relative sizes of different categories within a dataset.
Another trend is the use of percentages in personalized marketing. Companies analyze customer data to understand individual preferences and behaviors, and then use percentages to tailor marketing messages and offers. For instance, a retailer might send a customer a personalized email offering a 15% discount on their favorite product category.
However, there are also some challenges associated with the widespread use of percentages. One concern is the potential for misinterpretation or manipulation. Percentages can be easily manipulated to create a misleading impression. For example, a company might claim a significant percentage increase in sales, but fail to mention that the increase is from a very low base.
Another challenge is the need for statistical literacy. As percentages become increasingly prevalent in everyday life, it is important for people to develop the skills to critically evaluate percentage-based information. This includes understanding the limitations of percentages, recognizing potential biases, and being able to interpret percentages in context. Professional insights highlight the importance of context when interpreting percentages. For example, a small percentage change in a large market can have a significant impact, while a large percentage change in a small market might be relatively insignificant.
Furthermore, the use of AI and machine learning is enhancing the application of percentages in predictive analytics. Algorithms can analyze vast datasets to identify patterns and trends, and then use percentages to forecast future outcomes. For example, a financial institution might use machine learning to predict the likelihood of a loan default, expressed as a percentage.
Tips and Expert Advice: Mastering Percentage Calculations
Converting fractions to percentages is a straightforward process that can be mastered with a few simple tips and tricks. The most basic method involves dividing the numerator (the top number) by the denominator (the bottom number) and then multiplying the result by 100.
1. Simplify the Fraction: Before diving into the calculation, check if you can simplify the fraction. Simplifying the fraction makes the division easier and reduces the chances of errors. For example, if you have the fraction 4/8, you can simplify it to 1/2 by dividing both the numerator and denominator by 4. Then, dividing 1 by 2 gives you 0.5, which you then multiply by 100 to get 50%.
2. Use a Calculator: While it's important to understand the underlying concepts, don't hesitate to use a calculator for complex calculations. Calculators are especially useful when dealing with fractions that result in long or repeating decimals. Using a calculator can save you time and ensure accuracy.
3. Convert to Decimal First: As mentioned earlier, converting the fraction to a decimal before multiplying by 100 can make the process more intuitive. To convert a fraction to a decimal, simply divide the numerator by the denominator. For example, to convert 3/4 to a percentage, divide 3 by 4 to get 0.75. Then, multiply 0.75 by 100 to get 75%.
4. Practice Regularly: Like any mathematical skill, mastering percentage calculations requires practice. The more you practice, the more comfortable you will become with the process. Try working through different examples and scenarios to solidify your understanding. You can find practice problems online or in textbooks.
5. Understand the Context: Always consider the context in which you are using percentages. Percentages can be easily misinterpreted if they are taken out of context. For example, a 10% increase might sound impressive, but it could be insignificant if the starting value was very low.
6. Double-Check Your Work: It's always a good idea to double-check your work, especially when dealing with important calculations. Make sure you have correctly identified the "part" and the "whole" and that you have performed the calculations accurately.
7. Use Benchmarks: Create mental benchmarks for common percentages. Knowing that 1/4 is 25%, 1/2 is 50%, and 3/4 is 75% can help you quickly estimate percentages and identify potential errors.
Now, let's apply these tips to the original question: What is 5 out of 20 as a percentage?
First, we have the fraction 5/20. To simplify, we can divide both the numerator and denominator by 5, resulting in 1/4. Now, we can easily convert 1/4 to a decimal by dividing 1 by 4, which gives us 0.25. Finally, we multiply 0.25 by 100 to get 25%. Therefore, 5 out of 20 is equal to 25%. This practical example illustrates how simplifying the fraction can make the calculation much easier.
FAQ: Your Percentage Questions Answered
Q: How do I convert a percentage back to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, to convert 60% to a fraction, divide 60 by 100 to get 60/100. Then, simplify the fraction by dividing both the numerator and denominator by their greatest common divisor (in this case, 20), which gives you 3/5.
Q: What is the difference between percentage and percentage points?
A: Percentage refers to a proportion out of 100, while percentage points refer to the arithmetic difference between two percentages. For example, if a company's profit margin increased from 10% to 15%, the increase is 5 percentage points (15 - 10 = 5). It is also a 50% increase ((15-10)/10 * 100 = 50%).
Q: How do I calculate the percentage of a discount?
A: To calculate the percentage of a discount, divide the discount amount by the original price and multiply by 100. For example, if an item originally priced at $80 is on sale for $60, the discount amount is $20. Divide $20 by $80 (20/80 = 0.25) and multiply by 100 to get 25%. Therefore, the discount is 25%.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when calculating percentage increase. For example, if a company's revenue doubles, the percentage increase is 100%. If the revenue triples, the percentage increase is 200%, and so on.
Q: How are percentages used in statistics?
A: Percentages are widely used in statistics to represent proportions, distributions, and probabilities. They are often used to summarize data, compare different groups, and identify trends. For example, percentages are used to report survey results, election outcomes, and demographic data.
Conclusion: Mastering the Power of Percentages
Understanding and calculating percentages is a fundamental skill that is essential for navigating everyday life. From figuring out discounts to interpreting data, percentages are everywhere. By mastering the basic concepts, practicing regularly, and understanding the context in which percentages are used, you can unlock the power of percentages and make informed decisions. Knowing that 5 out of 20 is equal to 25% is just the beginning. The more you delve into the world of percentages, the more you will appreciate their versatility and usefulness.
Take the time to practice converting fractions to percentages, calculating percentage increases and decreases, and interpreting percentage-based information. The more comfortable you become with these skills, the more confident you will be in your ability to analyze and understand the world around you. Share this article with your friends and family, and let's all become more percentage-savvy!
Latest Posts
Latest Posts
-
Which Is Bigger Pint Or Quart
Nov 25, 2025
-
How Many Ounces Is In A Pound And A Half
Nov 25, 2025
-
Lord Of Flies Chapter 12 Summary
Nov 25, 2025
-
How Many Ounces Water In Gallon
Nov 25, 2025
-
What Is The Decimal For 5 8
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.