7 As A Percentage Of 20
sandbardeewhy
Nov 21, 2025 · 13 min read
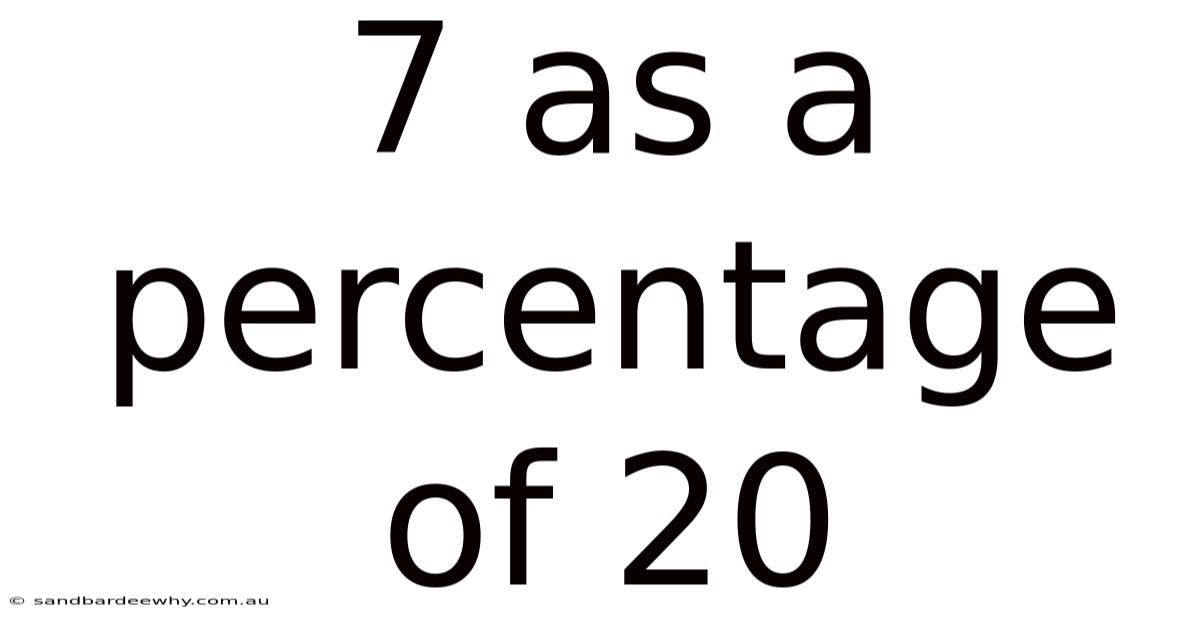
Table of Contents
Imagine you're at a bustling farmers market, eyeing a basket of vibrant red apples. The sign says, "20 Apples for $10!" You only want a few, so you pick out 7 apples. Now, you need to figure out what percentage of the entire basket you're taking so you can pay a fair price. How do you calculate what percentage 7 is of 20?
Understanding percentages is a fundamental skill that stretches far beyond the farmers market. It's essential in finance, statistics, everyday shopping, and even understanding scientific data. Whether you're calculating discounts, analyzing survey results, or determining proportions in a recipe, knowing how to work with percentages is crucial. Let's dive into a comprehensive exploration of how to calculate what 7 is as a percentage of 20, and how you can apply this knowledge to countless other scenarios.
Mastering Percentage Calculations: 7 as a Percentage of 20
Percentages are all about expressing a part of a whole in terms of 100. The term "percent" itself comes from the Latin per centum, meaning "out of one hundred." This means that when we say something is 50 percent, we're saying it's 50 out of every 100, or half of the total. To find what percentage one number is of another, we use a simple formula:
(Part / Whole) * 100 = Percentage
In our specific case, we want to find what percentage 7 is of 20. So, 7 is the "part," and 20 is the "whole." Plugging these values into the formula gives us:
(7 / 20) * 100 = Percentage
Now, let’s break down the calculation step by step. First, divide 7 by 20:
7 / 20 = 0.35
Next, multiply this result by 100 to convert the decimal to a percentage:
0.35 * 100 = 35%
Therefore, 7 is 35% of 20. This means that if you take 7 apples from a basket of 20, you're taking 35% of the total apples.
The Foundational Math Behind Percentages
Understanding the underlying math behind percentages helps solidify the concept and makes it easier to apply in various situations. Percentages are essentially fractions or ratios with a standardized denominator of 100. This standardization allows us to easily compare different proportions and understand relative sizes.
Consider a pie chart. The entire pie represents 100%, and each slice represents a percentage of the whole. If one slice takes up a quarter of the pie, it represents 25% (because 1/4 = 0.25, and 0.25 * 100 = 25%).
The formula (Part / Whole) * 100 is derived from the basic principles of fractions and ratios. The division (Part / Whole) gives you the fractional representation of the part in relation to the whole. Multiplying by 100 simply converts this fraction into a percentage. For example, if you scored 80 out of 100 on a test, the fraction is 80/100, which simplifies to 0.8. Multiplying 0.8 by 100 gives you 80%, which is your score as a percentage.
Historical Context of Percentages
The concept of percentages can be traced back to ancient Rome. As the Roman Empire expanded, they needed a standardized way to calculate taxes and financial transactions. The Romans often used fractions like 1/100 to compute taxes on goods sold at auction. This evolved into a system of hundredths, which laid the groundwork for what we now know as percentages.
During the Middle Ages, as trade and commerce flourished in Europe, the use of percentages became more widespread. Italian merchants, particularly in Florence and Venice, played a crucial role in developing and popularizing the concept. They used percentages to calculate interest rates, profits, and losses.
The symbol "%" is believed to have evolved from a symbol used to represent per cento (Italian for "out of one hundred"). Over time, this symbol was abbreviated and eventually transformed into the modern percentage sign. The standardization of percentages made financial calculations easier and more consistent, contributing to the growth of modern banking and finance.
Real-World Applications Beyond the Classroom
The ability to calculate percentages is not just an academic exercise; it's a practical skill that’s applicable in numerous real-world scenarios. From managing personal finances to making informed purchasing decisions, understanding percentages empowers you to make smarter choices.
In finance, percentages are used to calculate interest rates on loans and investments, as well as returns on investments. For example, if you invest $1,000 in a stock that increases in value by $50, the return on your investment is 5% (because (50 / 1000) * 100 = 5%). Understanding these percentages helps you evaluate the performance of your investments and make informed decisions about where to allocate your money.
In retail, percentages are used to calculate discounts and sales tax. When a store advertises a "20% off" sale, you can calculate the discounted price by multiplying the original price by 20% and subtracting that amount from the original price. Similarly, sales tax is calculated as a percentage of the purchase price and added to the total cost. Knowing how to calculate these percentages helps you determine the actual cost of items and compare prices across different stores.
In healthcare, percentages are used to express the effectiveness of treatments and the prevalence of diseases. For example, if a study shows that a new drug is 80% effective in treating a certain condition, it means that 80 out of 100 people who take the drug experience positive results. Understanding these percentages helps you evaluate the potential benefits and risks of different treatments.
Psychological Perspective
Numbers do not exist in a vacuum. Our brains respond to them based on context and presentation. For instance, behavioral economics teaches us that framing information as a percentage can significantly impact decision-making. A "10% discount" might seem more appealing than "saving $5 on a $50 item," even though they represent the same value. The human brain often perceives percentage discounts as larger relative savings.
The way a percentage is presented can also influence how we perceive risk and reward. For example, a "95% success rate" sounds far more reassuring than a "5% failure rate," even though they convey the same information. This psychological framing is used extensively in marketing, finance, and healthcare to influence consumer behavior and decision-making.
Understanding these psychological aspects of percentages can help you become a more critical and informed consumer. By recognizing how percentages can be used to manipulate perceptions, you can make more rational decisions based on the actual value or risk involved.
Trends and Latest Developments
In today's data-driven world, understanding percentages is more critical than ever. From financial analyses to scientific research, percentages are used to present and interpret data across a wide range of fields. Recent trends and developments highlight the increasing importance of this fundamental skill.
One notable trend is the use of percentages in data visualization. As the amount of available data continues to grow exponentially, it's becoming increasingly important to present this data in a way that is easy to understand and interpret. Percentages are often used in charts and graphs to show the relative proportions of different categories, making it easier to identify patterns and trends.
For example, pie charts and stacked bar charts are commonly used to visualize percentages. These types of charts allow you to quickly compare the sizes of different segments or categories and see how they contribute to the overall total. Data visualization tools often include features that automatically calculate and display percentages, making it easier for users to analyze and interpret data.
Another trend is the use of percentages in machine learning and artificial intelligence. Machine learning algorithms often use percentages to express the accuracy and reliability of their predictions. For example, a machine learning model might be said to have an accuracy rate of 90%, meaning that it correctly predicts the outcome 90% of the time. Understanding these percentages is crucial for evaluating the performance of machine learning models and determining whether they are suitable for a particular application.
Additionally, the proliferation of online tools and calculators has made it easier than ever to calculate percentages. These tools can be used to quickly perform complex calculations, such as calculating compound interest rates or determining the percentage change between two values. While these tools can be helpful, it's important to understand the underlying concepts and principles so that you can interpret the results accurately.
Professional Insights
From a professional standpoint, the ability to work with percentages is essential for anyone working in finance, marketing, or data analysis. Financial analysts use percentages to calculate returns on investments, analyze financial statements, and make investment recommendations. Marketers use percentages to track campaign performance, measure customer engagement, and analyze market trends. Data analysts use percentages to summarize data, identify patterns, and draw conclusions.
In finance, understanding percentages is crucial for evaluating the profitability and risk of different investment opportunities. For example, a financial analyst might use percentages to calculate the return on equity (ROE) or the debt-to-equity ratio. These metrics provide insights into a company's financial performance and help investors make informed decisions about whether to invest in the company.
In marketing, percentages are used to track the success of marketing campaigns and identify areas for improvement. For example, a marketer might use percentages to measure the click-through rate (CTR) of an online advertisement or the conversion rate of a landing page. These metrics provide insights into how well the campaign is performing and help marketers optimize their strategies to improve results.
In data analysis, percentages are used to summarize large datasets and identify meaningful patterns. For example, a data analyst might use percentages to calculate the proportion of customers who fall into different demographic categories or the percentage of sales that come from different product lines. These percentages can then be used to create reports and visualizations that communicate key findings to stakeholders.
Tips and Expert Advice
To truly master percentage calculations, especially when determining what 7 is as a percentage of 20, consider these practical tips and expert advice. These insights will help you apply the concepts more effectively in real-world scenarios.
Simplify Fractions
Before diving into the percentage calculation, simplify the fraction if possible. This can make the numbers easier to work with and reduce the chances of making errors. In our case, the fraction is 7/20, which is already in its simplest form. However, if you were working with a fraction like 12/30, you could simplify it to 2/5 by dividing both the numerator and denominator by their greatest common divisor, which is 6.
Simplifying fractions not only makes the calculations easier but also helps you understand the relationship between the part and the whole more intuitively. For example, knowing that 12/30 is equivalent to 2/5 tells you that the part is two-fifths of the whole.
Estimate Before Calculating
Before performing the calculation, take a moment to estimate the percentage. This can help you catch any obvious errors and ensure that your final answer is reasonable. In our case, we know that 7 is a little more than one-third of 20. Since one-third is approximately 33.33%, we can estimate that the percentage should be somewhere around 35%.
Estimating before calculating also helps you develop a better understanding of percentages and how they relate to fractions and ratios. By mentally approximating the percentage, you can improve your number sense and make more informed decisions in real-world scenarios.
Use Benchmarks
Use common benchmarks to help you visualize and understand percentages. For example, 25% is equivalent to one-quarter, 50% is equivalent to one-half, and 75% is equivalent to three-quarters. These benchmarks can serve as reference points when you are estimating or calculating percentages.
In our case, we can use the benchmark of 50% to help us understand that 7 is less than half of 20. This reinforces our understanding that the percentage should be less than 50%. Using benchmarks can also help you quickly estimate percentages in everyday situations, such as calculating discounts or tipping at a restaurant.
Practice Regularly
The best way to master percentage calculations is to practice regularly. The more you practice, the more comfortable you will become with the concepts and the more easily you will be able to apply them in different situations. Try working through practice problems, solving real-world scenarios, and using online tools and calculators to test your skills.
You can also practice by incorporating percentage calculations into your daily life. For example, you can calculate the percentage discount on items you purchase, track your expenses as a percentage of your income, or estimate the percentage of time you spend on different activities each day. By making percentage calculations a regular part of your routine, you can develop a strong understanding of the concepts and improve your ability to apply them in any situation.
FAQ
Q: How do I convert a percentage back to a fraction? A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 35% is equal to 35/100, which simplifies to 7/20.
Q: Can a percentage be greater than 100%? A: Yes, a percentage can be greater than 100%. This typically occurs when you are comparing a value to its original value and the value has increased by more than the original amount. For example, if a company's revenue increases from $100,000 to $150,000, the revenue has increased by 50%, but the new revenue is 150% of the original revenue.
Q: How do I calculate the percentage increase or decrease between two values? A: To calculate the percentage increase or decrease between two values, use the formula: ((New Value - Old Value) / Old Value) * 100. If the result is positive, it represents a percentage increase. If the result is negative, it represents a percentage decrease.
Q: What is the difference between a percentage point and a percentage? A: A percentage point is the arithmetic difference between two percentages. For example, if a company's profit margin increases from 10% to 12%, the profit margin has increased by 2 percentage points. The percentage increase in the profit margin is ((12-10)/10) * 100 = 20%.
Q: How are percentages used in statistics? A: In statistics, percentages are used to summarize and analyze data, calculate probabilities, and make inferences about populations. Percentages are often used to express the proportion of a sample that falls into a particular category or to compare the characteristics of different groups.
Conclusion
In summary, determining that 7 is 35% of 20 involves understanding the basic formula (Part / Whole) * 100 and applying it correctly. Percentages are a fundamental concept with wide-ranging applications in finance, retail, healthcare, and everyday life. By mastering percentage calculations, you can make more informed decisions, analyze data more effectively, and improve your overall numerical literacy.
Now that you have a solid understanding of how to calculate percentages, put your knowledge to the test. Try applying these concepts in your daily life, whether it's calculating discounts while shopping, analyzing your personal finances, or interpreting data in the news. Share your findings with others and help them improve their understanding of percentages as well. What everyday scenarios can you apply this knowledge to? Leave a comment below and let's discuss how we can all become more proficient with percentages!
Latest Posts
Latest Posts
-
Why Did Gatsby Buy His House
Nov 21, 2025
-
What Area In The Brain Sets The Respiratory Rhythm
Nov 21, 2025
-
Inverse Operations To Isolate The Variable Examples
Nov 21, 2025
-
How Do You Factor A Trinomial
Nov 21, 2025
-
Why Are Fruit Flies Biting Me
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 7 As A Percentage Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.