7 Is What Percent Of 20
sandbardeewhy
Nov 28, 2025 · 11 min read
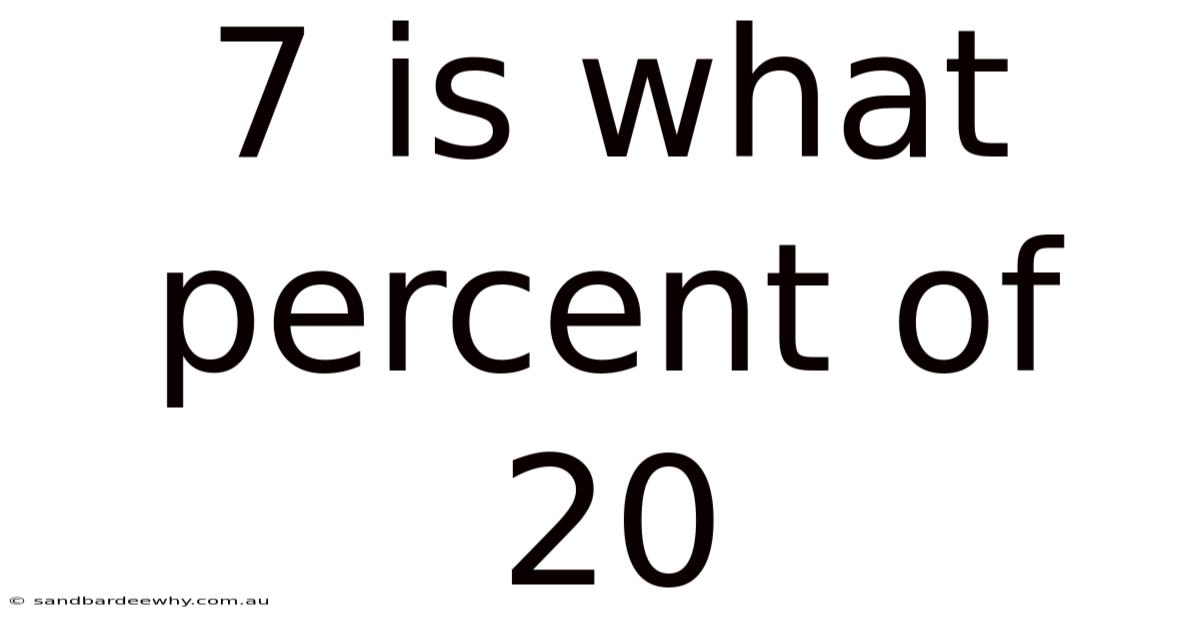
Table of Contents
Imagine you're at a bustling farmer's market, and you've decided to buy some delicious apples. You pick out a basket of 20 shiny, red apples. As you're about to pay, the farmer tells you that 7 of these apples are a special variety, grown only on his farm. Curious, you wonder: "What percentage of my apples are these special ones?"
This simple scenario introduces us to a fundamental concept used daily: calculating percentages. Whether figuring out discounts while shopping, understanding statistics in a report, or determining proportions in recipes, percentages are everywhere. In this article, we will explore how to solve the specific problem of finding what percentage 7 is of 20. We'll break down the concept, provide step-by-step instructions, offer real-world examples, and answer common questions to ensure you fully grasp the concept.
Understanding the Basics of Percentages
To determine what percent 7 is of 20, we need to understand what a percentage represents. A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." Thus, when we say "50 percent," we mean 50 out of 100, or half.
The Formula for Calculating Percentages
The basic formula for calculating a percentage is:
(Part / Whole) * 100 = Percentage
- Part: The specific amount you are interested in (in our case, 7).
- Whole: The total amount or the reference value (in our case, 20).
- Percentage: The result you get after performing the calculation, expressed as a percentage.
Applying the Formula to "7 is What Percent of 20"
Using the formula, we can set up our equation as follows:
(7 / 20) * 100 = Percentage
Now, let's break down the calculation step-by-step:
-
Divide the Part by the Whole:
7 ÷ 20 = 0.35
-
Multiply by 100:
- 35 * 100 = 35
So, 7 is 35% of 20.
Historical Context of Percentages
The concept of percentages has ancient roots. Historians believe that the idea of using hundredths originated in ancient Rome, where taxes were often calculated as a certain number of centesimae (hundredths) of the value of goods. As trade and commerce grew, the need for a standardized way to express proportions became increasingly important.
During the Middle Ages, the use of percentages became more widespread in Europe, particularly in Italy, where merchants used them for calculating interest, profits, and losses. By the 15th century, the percentage symbol (%) began to appear, further solidifying its place in mathematical and commercial practices.
Why Percentages Are Important
Percentages are an essential tool in various fields:
- Finance: Calculating interest rates, investment returns, and loan payments.
- Retail: Determining discounts, markups, and sales tax.
- Statistics: Expressing data and survey results in a standardized way.
- Science: Representing concentrations, errors, and changes in experimental data.
- Everyday Life: Figuring out tips, understanding nutritional information, and comparing prices.
Common Misconceptions About Percentages
-
Confusing Percentage with Percentage Points: It's important to distinguish between a percentage and a percentage point. A percentage is a relative value, while a percentage point is an absolute difference between two percentages. For example, if a value increases from 10% to 12%, it has increased by 2 percentage points, but it has increased by 20% (since 2 is 20% of 10).
-
Incorrectly Calculating Percentage Change: When calculating percentage change, always use the initial value as the denominator. The formula is:
((New Value - Initial Value) / Initial Value) * 100 -
Applying Percentages to Different Wholes: Be careful when comparing percentages that are based on different totals. For example, a 10% discount on a $100 item is different from a 10% discount on a $200 item.
Real-World Examples and Applications
Understanding how to calculate percentages is useful in various scenarios. Let's explore a few real-world examples where determining what percent one number is of another can be beneficial.
Example 1: Calculating Test Scores
Suppose you took a test with 20 questions, and you answered 7 questions correctly. What percentage of the questions did you get right?
Using the formula:
(7 / 20) * 100 = 35%
You answered 35% of the questions correctly.
Example 2: Budgeting Finances
Let's say you have a monthly budget of $20, and you spend $7 on entertainment. What percentage of your budget is allocated to entertainment?
Using the formula:
(7 / 20) * 100 = 35%
You spend 35% of your budget on entertainment.
Example 3: Analyzing Sales Data
A store sold 20 products in a day, and 7 of them were sold during a promotional period. What percentage of the day's sales came from the promotional period?
Using the formula:
(7 / 20) * 100 = 35%
35% of the day's sales came from the promotional period.
Example 4: Determining Dietary Composition
If a snack contains 20 grams of total carbohydrates, and 7 grams of that are fiber, what percentage of the carbohydrates is fiber?
Using the formula:
(7 / 20) * 100 = 35%
35% of the carbohydrates in the snack are fiber.
Example 5: Assessing Project Completion
You have a project that requires 20 tasks to complete, and you have finished 7 tasks. What percentage of the project is complete?
Using the formula:
(7 / 20) * 100 = 35%
You have completed 35% of the project.
Trends and Latest Developments
The use of percentages remains a fundamental part of data analysis and reporting across various sectors. However, the way percentages are used and interpreted is evolving with the rise of data science and analytics.
Visual Representation of Percentages
Modern data visualization tools provide interactive ways to represent percentages, making it easier to understand and communicate insights. Pie charts, bar graphs, and dashboards are commonly used to display percentage distributions, allowing users to quickly grasp the proportions of different categories.
The Role of Technology
Technology has made calculating percentages more accessible and efficient. Spreadsheet software like Microsoft Excel and Google Sheets offer built-in functions to calculate percentages automatically. Statistical software packages like R and Python provide advanced tools for analyzing and visualizing percentage data.
Behavioral Insights
Behavioral economics has highlighted the importance of how percentages are framed and presented. For example, studies have shown that people are more likely to respond positively to a 90% success rate than a 10% failure rate, even though they represent the same information. Understanding these psychological effects is crucial in marketing, advertising, and public policy.
Big Data and Analytics
In the era of big data, percentages play a critical role in summarizing and interpreting large datasets. Data analysts use percentages to identify trends, patterns, and anomalies in vast amounts of information, helping organizations make data-driven decisions.
Expert Insight on Using Percentages Effectively
"Percentages are powerful tools for simplifying complex data, but they must be used with caution," says Dr. Emily Carter, a statistician at Data Insights Analytics. "Always consider the context and the base value when interpreting percentages. Misleading conclusions can arise if percentages are used without understanding the underlying data."
Tips and Expert Advice
To effectively use and understand percentages, here are some practical tips and expert advice:
1. Always Know Your Base
When interpreting a percentage, always be aware of the base value it refers to. A small percentage of a large number can still be significant, while a large percentage of a small number may be relatively insignificant.
For example, a 1% increase in the sales of a company with $1 billion in revenue is a substantial $10 million increase. On the other hand, a 50% increase in the sales of a small business with $10,000 in revenue is only a $5,000 increase.
2. Use Percentages to Compare Proportions
Percentages are useful for comparing proportions, but ensure you are comparing them within a consistent context. Avoid comparing percentages that are calculated based on different bases or populations.
For instance, comparing the percentage of students passing a test in two different schools is valid only if the schools have similar student demographics and testing standards. If one school has a more selective admission process, a direct comparison of pass rates may be misleading.
3. Be Mindful of Percentage Change
When calculating percentage change, use the correct formula and always refer to the initial value as the base. Incorrectly calculating percentage change can lead to significant misinterpretations.
For example, if a product's price increases from $20 to $25, the percentage increase is:
(($25 - $20) / $20) * 100 = 25%
4. Avoid Averaging Percentages
Averaging percentages directly can be misleading if the bases are different. Instead, calculate the weighted average by considering the base values.
For example, if one class has a 70% pass rate with 30 students and another class has an 80% pass rate with 20 students, the overall pass rate is not simply the average of 70% and 80%. Instead, calculate the total number of students who passed and divide by the total number of students:
((0.70 * 30) + (0.80 * 20)) / (30 + 20) = (21 + 16) / 50 = 37 / 50 = 0.74 = 74%
The overall pass rate is 74%.
5. Use Visualization Tools
Employ data visualization tools like charts and graphs to present percentages effectively. Visual representations can make it easier to understand and communicate percentage data, especially when dealing with complex information.
For example, a pie chart can clearly show the distribution of a budget across different categories, while a bar graph can compare the percentages of different groups.
6. Understand Contextual Relevance
Always consider the context when interpreting percentages. A percentage may have different implications depending on the situation.
For example, a 5% error rate in a medical diagnosis could have severe consequences, while a 5% error rate in a customer satisfaction survey might be acceptable.
7. Round Appropriately
When presenting percentages, round the numbers appropriately to avoid giving a false sense of precision. In many cases, rounding to the nearest whole number or tenth of a percent is sufficient.
For example, instead of saying 35.2857%, round it to 35.3% or even 35%, depending on the level of detail required.
8. Double-Check Your Calculations
Always double-check your calculations to ensure accuracy. Even a small error can lead to significant misinterpretations.
Use a calculator or spreadsheet software to verify your results, and if possible, have someone else review your work.
9. Communicate Clearly
When presenting percentages, communicate clearly and concisely. Explain what the percentage represents and provide any relevant context.
Avoid using jargon or technical terms that the audience may not understand. Use simple language and visual aids to enhance understanding.
10. Stay Updated
Keep yourself updated with the latest developments in data analysis and statistics. As technology and methodologies evolve, new tools and techniques for using percentages effectively may emerge.
FAQ
Q: How do I convert a percentage to a decimal?
A: To convert a percentage to a decimal, divide the percentage by 100. For example, 35% becomes 35 / 100 = 0.35.
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.35 becomes 0.35 * 100 = 35%.
Q: What is the difference between a percentage increase and a percentage decrease?
A: A percentage increase represents the relative increase in a value, while a percentage decrease represents the relative decrease. The formulas are:
- Percentage Increase:
((New Value - Initial Value) / Initial Value) * 100 - Percentage Decrease:
((Initial Value - New Value) / Initial Value) * 100
Q: How do I calculate a percentage of a number?
A: To calculate a percentage of a number, convert the percentage to a decimal and multiply it by the number. For example, to find 35% of 200:
0.35 * 200 = 70
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an initial value and the new value is more than double the initial value. For example, if a company's revenue increases from $100 to $250, the percentage increase is:
(($250 - $100) / $100) * 100 = 150%
Q: How do I calculate the original value if I know the percentage and the result?
A: To calculate the original value, divide the result by the percentage (expressed as a decimal). For example, if 35% of a number is 70, the original number is:
70 / 0.35 = 200
Conclusion
In summary, understanding what percent 7 is of 20 involves a simple yet powerful calculation. By dividing the part (7) by the whole (20) and multiplying by 100, we find that 7 is 35% of 20. This fundamental concept is applicable in various real-world scenarios, from calculating test scores and budgeting finances to analyzing sales data and determining dietary composition. By mastering the use of percentages, you can enhance your analytical skills and make more informed decisions in both personal and professional contexts.
Now that you have a solid understanding of how to calculate percentages, put your knowledge to the test! Try applying the formula to different scenarios and see how percentages can help you make sense of the world around you. Share your findings, ask questions, and engage with others to deepen your understanding and unlock the full potential of this essential mathematical tool.
Latest Posts
Latest Posts
-
How Do You Find The Quotient Of A Fraction
Nov 28, 2025
-
What Is The Meaning Of Character Traits
Nov 28, 2025
-
Symbolism In The Most Dangerous Game
Nov 28, 2025
-
How Many Cups Is A Half Gallon Of Water
Nov 28, 2025
-
How Do You Use Triple Beam Balance
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about 7 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.