8 Of 12 Is What Percent
sandbardeewhy
Nov 28, 2025 · 10 min read
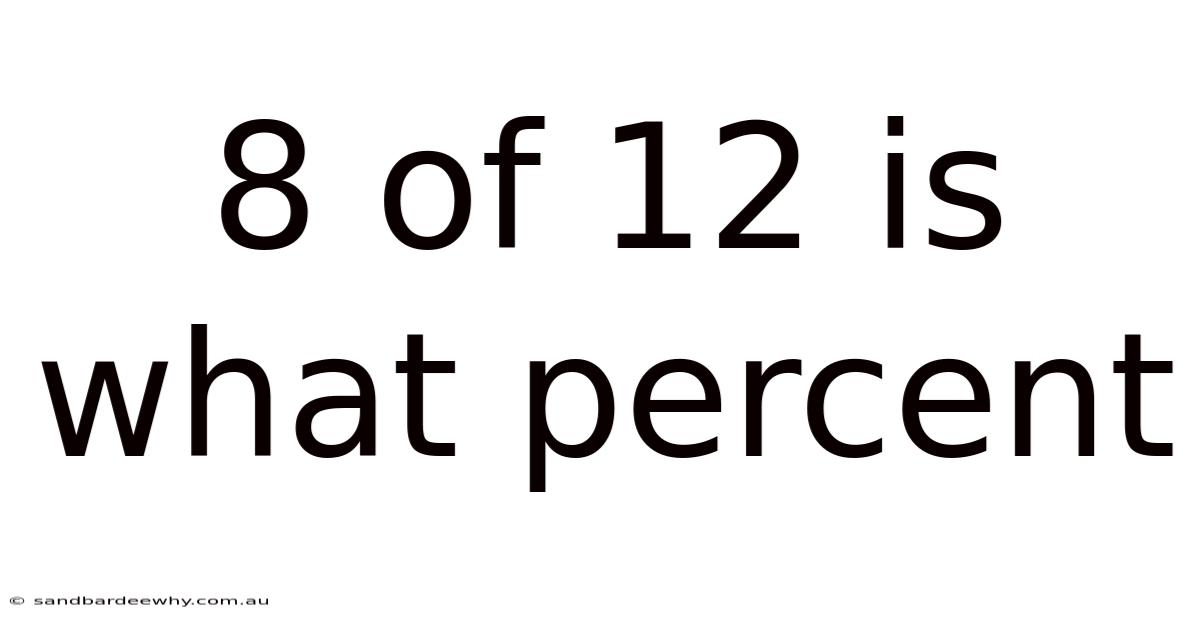
Table of Contents
Have you ever found yourself calculating discounts at a store, figuring out a tip at a restaurant, or trying to understand sports statistics? These everyday scenarios often require a quick grasp of percentages. What seems like a simple calculation can sometimes be confusing. For instance, consider this question: 8 of 12 is what percent? While it may appear straightforward, understanding the underlying principles and methods to solve it is crucial. Let's dive into this fundamental concept and explore how to accurately calculate percentages in various contexts.
Decoding Percentage Basics
Percentages are a fundamental part of mathematics, crucial in daily life and various professional fields. To truly grasp "8 of 12 is what percent," it’s important to break down the basics. A percentage is a way of expressing a number as a fraction of 100. In simpler terms, it's a ratio that tells us how much of one quantity we have relative to a whole, with that whole always being considered as 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." This concept allows us to standardize comparisons and understand proportions more intuitively.
Imagine you have a pie cut into 100 slices. If you eat 25 slices, you've consumed 25 percent of the pie. Percentages are used to represent this kind of proportional relationship, making it easier to compare different quantities regardless of their absolute sizes. This is why percentages are preferred in many situations, from calculating interest rates on loans to understanding the results of a survey. By understanding this basic idea, you can appreciate why percentages are so useful in analyzing data, making decisions, and communicating information effectively.
Delving Deeper: The Foundation of Percentages
At its core, understanding percentages means recognizing that they are essentially fractions or ratios with a standard denominator of 100. This standardization allows for straightforward comparisons and calculations. When we say something is "50 percent," we mean it is 50 out of 100, which can also be expressed as the fraction 50/100 or the decimal 0.5. This interconvertibility between percentages, fractions, and decimals is a key aspect of working with percentages effectively.
The concept of percentages has ancient roots, dating back to the Roman Empire, where taxes were often calculated as a fraction of assets. Over time, as trade and commerce expanded, the need for a standardized way to express proportions became increasingly important. The development of the percent symbol (%) and the widespread use of percentages in calculations helped to streamline financial transactions and data analysis. Today, percentages are used in virtually every aspect of life, from personal finance to scientific research, demonstrating their enduring relevance and utility. Grasping the underlying mathematical principles allows for a more intuitive understanding and confident application of percentages in various real-world scenarios.
The Practical Applications of Percentages
Percentages are not just theoretical concepts; they are essential tools in everyday life. Consider shopping: Discounts are almost always expressed as percentages. For instance, a "20% off" sale means that an item's price is reduced by 20 percent of its original value. Knowing how to calculate this discount quickly can save you money and ensure you're getting a good deal. Similarly, when dining out, understanding how to calculate a tip as a percentage of the bill is crucial for proper etiquette and financial planning.
In finance, percentages are used to represent interest rates on loans and investments, inflation rates, and the performance of stock portfolios. Understanding these percentages can help you make informed decisions about saving, investing, and managing your money. In statistics, percentages are used to present data in a clear and understandable format. Survey results, market share, and demographic data are often expressed as percentages to highlight proportions and trends. By mastering the use of percentages, you equip yourself with a valuable skill set that enhances your ability to navigate the complexities of modern life and make informed decisions in various contexts.
Methods to Calculate Percentages
Calculating percentages can be straightforward once you understand the basic formulas and techniques. The most common method involves setting up a proportion or using a simple formula. To find what percentage one number is of another, you can use the formula: (Part / Whole) * 100. In the case of "8 of 12 is what percent," 8 is the part, and 12 is the whole. So, the calculation would be (8 / 12) * 100.
Another useful technique is to convert the percentage problem into an equation. For example, "What is 20% of 50?" can be written as "x = 0.20 * 50," where x is the unknown value. Solving for x gives you the answer. Additionally, understanding how to use mental math tricks can speed up percentage calculations in everyday situations. For instance, to find 10% of a number, simply move the decimal point one place to the left. To find 5%, take half of the 10% value. These methods and tricks can help you approach percentage problems with confidence and accuracy, whether you're calculating discounts, analyzing data, or making financial decisions.
The Role of Percentages in Decision-Making
Percentages play a critical role in decision-making across various fields. In business, companies use percentages to analyze market trends, track sales performance, and assess profitability. For instance, calculating the percentage increase or decrease in sales from one period to another can provide valuable insights into the effectiveness of marketing strategies and overall business performance. Similarly, analyzing the percentage of customer satisfaction can help identify areas for improvement in products or services.
In healthcare, percentages are used to communicate the effectiveness of treatments, assess the risk of diseases, and monitor patient outcomes. For example, a study might report that a new drug has a "90% success rate," indicating that it was effective in 90 percent of the cases. This kind of information helps doctors and patients make informed decisions about treatment options. In public policy, percentages are used to analyze demographic trends, assess the impact of government programs, and allocate resources effectively. Understanding how to interpret and use percentages in these contexts is essential for making informed decisions that are based on data and evidence. By mastering the use of percentages, you can enhance your ability to analyze information, identify trends, and make sound judgments in a variety of professional and personal settings.
Calculating "8 of 12 is What Percent?"
Let's apply the principles discussed above to solve the problem: "8 of 12 is what percent?" Here's a breakdown of the steps:
-
Identify the Part and the Whole: In this question, 8 is the part, and 12 is the whole. We want to find out what percentage 8 represents out of 12.
-
Set Up the Fraction: Express the relationship as a fraction: 8/12.
-
Convert to Decimal: Divide the numerator (8) by the denominator (12): 8 ÷ 12 ≈ 0.6667.
-
Convert to Percentage: Multiply the decimal by 100 to convert it to a percentage: 0.6667 * 100 = 66.67%.
So, 8 of 12 is approximately 66.67%.
Trends and Latest Developments
The way we calculate and use percentages has evolved with technological advancements. Today, calculators and software automate complex percentage calculations, making them faster and more accurate. However, understanding the underlying principles remains crucial, especially in data analysis and interpretation.
Visual Data Representation
Visual data representation is increasingly important. Charts, graphs, and infographics make understanding percentages easier, particularly in business and marketing. Presenting percentage data visually can quickly convey trends and insights that might be missed in raw numbers.
Statistical Analysis
Statistical analysis increasingly relies on percentages to provide meaningful insights. Market research, financial analysis, and scientific studies use percentages to present findings in an easily understandable format. For example, A/B testing in marketing often uses percentages to show which version of an ad performs better.
Machine Learning
Machine learning algorithms use percentages to assess model accuracy. Metrics like precision, recall, and F1-score, often expressed as percentages, help evaluate the performance of machine learning models.
Infographics
Infographics are valuable tools for presenting percentage data. By using visually appealing charts and graphs, infographics can simplify complex information and make it more accessible to a wider audience. They are particularly useful in marketing and education.
Tips and Expert Advice
Calculating percentages accurately requires careful attention to detail. Here are some tips and expert advice to help you avoid common mistakes and improve your skills.
Double-Check Your Work
Always double-check your calculations. A simple mistake in division or multiplication can lead to a significantly incorrect result. Use a calculator to verify your answers, especially when dealing with complex numbers.
Understand the Context
Pay attention to the context of the problem. Misunderstanding the question can lead to using the wrong numbers or applying the wrong formulas.
Use Estimation
Before doing the actual calculation, estimate the result. This will help you identify if your final answer is reasonable. For example, if you are calculating a percentage and expect the result to be around 50%, an answer of 5% or 500% should immediately raise a red flag.
Practice Regularly
Practice makes perfect. The more you work with percentages, the more comfortable and confident you will become. Try solving different types of percentage problems to expand your skill set.
Familiarize Yourself with Different Types of Percentage Problems
Understanding the different types of percentage problems—such as percentage increase, percentage decrease, and finding a percentage of a total—is crucial for accuracy. Each type requires a slightly different approach.
Utilize Online Resources
There are numerous online tools and resources available to help you practice and improve your percentage calculation skills. Websites, apps, and tutorials can provide additional support and guidance.
FAQ
Q: What is the formula for calculating percentage increase?
A: The formula for percentage increase is: [(New Value - Original Value) / Original Value] * 100.
Q: How do I calculate a percentage decrease?
A: The formula for percentage decrease is: [(Original Value - New Value) / Original Value] * 100.
Q: What is the difference between a percentage and a percentile?
A: A percentage represents a part of a whole, while a percentile indicates the value below which a given percentage of observations in a group of observations fall.
Q: How can I quickly calculate 10% of a number?
A: To find 10% of a number, simply move the decimal point one place to the left. For example, 10% of 50 is 5.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100% when dealing with percentage increase or when comparing a part to a whole that is smaller than the part.
Conclusion
Calculating percentages is a crucial skill applicable in numerous real-world scenarios, from everyday shopping to complex financial analysis. To answer the question, 8 of 12 is what percent?, we've shown it's approximately 66.67%. By understanding the basic principles, utilizing effective calculation methods, and staying informed about the latest trends, you can confidently tackle any percentage-related challenge.
Now that you have a solid grasp of percentages, put your knowledge into practice. Start by calculating discounts on your next shopping trip or figuring out tips at a restaurant. Share this article with friends or colleagues who might find it helpful. Leave a comment below with any questions or insights you've gained. Your engagement will not only reinforce your learning but also help others master this essential skill.
Latest Posts
Latest Posts
-
Is Melting Ice A Chemical Change
Nov 28, 2025
-
How Many Cups Are 200 Ml
Nov 28, 2025
-
How Much Is 200 C In Fahrenheit
Nov 28, 2025
-
Themes Of The Novel To Kill A Mockingbird
Nov 28, 2025
-
What Height Is 54 Inches In Feet
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about 8 Of 12 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.