Is 1 4 Greater Than 1 2
sandbardeewhy
Nov 28, 2025 · 12 min read
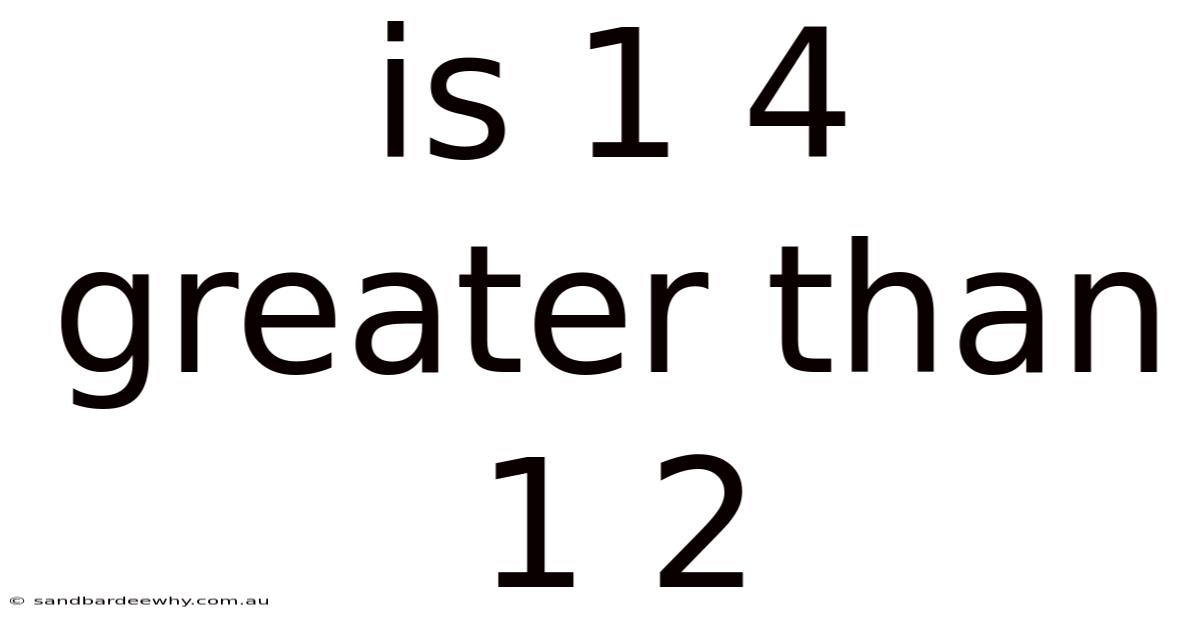
Table of Contents
Imagine you're sharing a pizza with a friend. You cut the pizza into four equal slices, and you get to eat one of those slices. Now, imagine you cut the same pizza into only two slices, and you get one of those slices. Which slice would you rather have? This simple scenario illustrates a fundamental concept in mathematics: comparing fractions.
At first glance, the numbers "4" and "2" might trick our minds into thinking that 1/4 is greater than 1/2, since 4 is bigger than 2. However, fractions represent parts of a whole, and the larger the denominator (the bottom number), the more pieces the whole is divided into, resulting in smaller individual pieces. So, is 1/4 greater than 1/2? Let's dive into a detailed exploration to understand why the answer is unequivocally no.
Understanding Fractions: Is 1/4 Greater Than 1/2?
To properly address the question of whether 1/4 is greater than 1/2, it’s essential to understand the basic principles of fractions. A fraction represents a part of a whole. It consists of two main components: the numerator and the denominator. The numerator (the top number) indicates how many parts of the whole you have, and the denominator (the bottom number) indicates how many equal parts the whole is divided into.
In the fraction 1/4, '1' is the numerator, and '4' is the denominator. This means we have one part out of a total of four equal parts. Similarly, in the fraction 1/2, '1' is the numerator, and '2' is the denominator, indicating that we have one part out of two equal parts. Visualizing these fractions can make the comparison much easier. Imagine a pie cut into four slices; 1/4 represents one of those slices. Now, picture the same pie cut into two slices; 1/2 represents one of these larger slices.
The Core Concept: Denominator Size
The key concept to grasp when comparing fractions is that the larger the denominator, the smaller the individual parts, assuming the numerator remains constant. When a whole is divided into more parts, each part naturally becomes smaller. Think of it this way: if you share a cake with four people, each person gets a smaller piece than if you shared the same cake with only two people.
Mathematically, this is a crucial point. The denominator determines the size of each fractional part. Therefore, a larger denominator means smaller parts, and a smaller denominator means larger parts. This inverse relationship is fundamental to understanding why 1/4 is not greater than 1/2.
Historical Context and Development of Fractions
The concept of fractions dates back to ancient civilizations. Egyptians used fractions extensively for measurement, land division, and accounting. Their system primarily used unit fractions (fractions with a numerator of 1), such as 1/2, 1/3, 1/4, and so on. The Babylonians, on the other hand, used a base-60 number system, which allowed them to represent fractions with greater accuracy, especially in astronomical calculations.
Over time, different cultures developed various notations and methods for working with fractions. The modern notation we use today, with a horizontal line separating the numerator and denominator, became standardized during the medieval period. Arab mathematicians made significant contributions to the understanding and manipulation of fractions, and their work was later transmitted to Europe, where it played a crucial role in the development of algebra and calculus.
Comparing Fractions: Methods and Techniques
Several methods can be used to compare fractions effectively. Here are some of the most common techniques:
-
Common Denominator Method: This involves finding a common denominator for both fractions. Once the denominators are the same, you can directly compare the numerators. The fraction with the larger numerator is the greater fraction. For example, to compare 1/4 and 1/2, you can convert 1/2 to 2/4. Now, comparing 1/4 and 2/4 is straightforward: 2/4 is larger.
-
Cross-Multiplication Method: This technique involves multiplying the numerator of one fraction by the denominator of the other fraction and vice versa. Then, you compare the resulting products. For example, to compare 1/4 and 1/2, multiply 1 (numerator of the first fraction) by 2 (denominator of the second fraction), which equals 2. Then, multiply 1 (numerator of the second fraction) by 4 (denominator of the first fraction), which equals 4. Since 4 is greater than 2, 1/2 is greater than 1/4.
-
Decimal Conversion: Convert both fractions to their decimal equivalents and then compare the decimal values. For example, 1/4 is equal to 0.25, and 1/2 is equal to 0.5. Comparing 0.25 and 0.5 clearly shows that 0.5 is larger.
-
Visual Aids: Using diagrams, such as pie charts or bar models, can provide a visual representation of the fractions, making it easier to compare their sizes. This is particularly helpful for students who are just learning about fractions.
Mathematical Representation and Proof
To mathematically prove that 1/2 is greater than 1/4, we can use the concept of inequalities. An inequality is a mathematical statement that shows the relationship between two values that are not equal. We want to show that:
1/4 < 1/2
To do this, we can multiply both sides of the inequality by a positive number without changing the direction of the inequality. Let's multiply both sides by 4:
4 * (1/4) < 4 * (1/2)
This simplifies to:
1 < 2
Since 1 is indeed less than 2, the original inequality 1/4 < 1/2 holds true. This provides a formal mathematical proof that 1/2 is greater than 1/4.
Current Trends and Data on Understanding Fractions
In education, there's a renewed emphasis on ensuring students develop a strong conceptual understanding of fractions. Traditional methods often focus on rote memorization of rules, which can lead to misunderstandings and difficulties when students encounter more complex mathematical concepts. Current pedagogical trends advocate for using visual models, real-world examples, and hands-on activities to help students grasp the underlying principles of fractions.
Recent studies have shown that students who have a strong conceptual understanding of fractions perform better in algebra and other advanced math courses. This highlights the importance of building a solid foundation in fraction concepts early in a student's mathematical education. Educational researchers are continually exploring new ways to improve fraction instruction and address common misconceptions.
One popular opinion among educators is that fractions should be introduced using concrete materials before moving on to abstract symbols. This approach helps students connect the abstract symbols to real-world objects and situations, making the concepts more meaningful and memorable. For instance, using fraction bars, pattern blocks, or even cutting up food items can help students visualize fractions and understand their relationships.
The Role of Technology in Teaching Fractions
Technology plays an increasingly important role in teaching fractions. Interactive simulations, educational apps, and online games can provide students with engaging and personalized learning experiences. These tools can help students explore fractions in a dynamic and interactive way, allowing them to manipulate virtual objects, solve problems, and receive immediate feedback.
For example, many educational websites offer virtual fraction manipulatives that students can use to compare fractions, add and subtract fractions, and solve fraction-related problems. These virtual tools can be particularly helpful for students who struggle with abstract concepts, as they provide a visual and interactive way to explore the properties of fractions.
Addressing Common Misconceptions
One of the most common misconceptions about fractions is that a larger denominator always means a larger fraction. As we've discussed, this is not true. The denominator represents the number of equal parts the whole is divided into, so a larger denominator actually means smaller parts. Another common misconception is that fractions must always be less than 1. Students may struggle to understand improper fractions (where the numerator is greater than the denominator) and mixed numbers.
To address these misconceptions, it's important to provide students with ample opportunities to work with fractions in a variety of contexts. Using visual models, real-world examples, and hands-on activities can help students develop a deeper understanding of fraction concepts and avoid common pitfalls.
Tips and Expert Advice for Mastering Fractions
Mastering fractions is crucial for success in mathematics and many real-world applications. Here are some practical tips and expert advice to help you or your students build a solid understanding of fractions:
1. Start with Visuals
Visual aids are invaluable when introducing fractions. Use diagrams, pie charts, bar models, and real-world objects to illustrate the concept of fractions. For example, when explaining 1/4 and 1/2, draw two identical circles. Divide one circle into four equal parts and shade one part to represent 1/4. Divide the other circle into two equal parts and shade one part to represent 1/2. Visually comparing the shaded areas clearly shows that 1/2 is larger than 1/4.
Encourage learners to draw their own diagrams to represent fractions. This active engagement reinforces their understanding and helps them visualize the relationship between the numerator and denominator. Additionally, use physical objects like building blocks or measuring cups to demonstrate fractions in a tangible way.
2. Emphasize Real-World Connections
Connect fractions to real-world situations to make the concepts more relevant and meaningful. For example, when discussing 1/2, talk about sharing a pizza with a friend or cutting a sandwich in half. When discussing 1/4, talk about dividing a cake into four equal pieces or measuring ingredients for a recipe.
By relating fractions to everyday experiences, learners can better understand their practical applications and see the value of learning about them. Encourage learners to identify fractions in their own environment, such as in cooking, measuring, or telling time.
3. Practice with Manipulatives
Hands-on activities with manipulatives can greatly enhance understanding. Fraction bars, pattern blocks, and Cuisenaire rods are excellent tools for exploring fraction concepts. These manipulatives allow learners to physically manipulate fractions, compare their sizes, and perform operations.
For example, using fraction bars, learners can easily compare 1/4 and 1/2 by placing the corresponding bars side by side. This visual comparison reinforces the understanding that 1/2 is larger than 1/4. Encourage learners to experiment with different manipulatives and explore various fraction concepts through hands-on activities.
4. Focus on Conceptual Understanding
Avoid rote memorization of rules without understanding the underlying concepts. Instead, focus on building a strong conceptual foundation. For example, when teaching fraction operations, explain why we need a common denominator before adding or subtracting fractions.
Help learners understand the meaning of the numerator and denominator and how they relate to each other. Encourage them to explain their reasoning and justify their answers. By emphasizing conceptual understanding, learners will be better equipped to apply their knowledge to solve complex problems.
5. Use Technology Wisely
Technology can be a powerful tool for learning fractions, but it should be used strategically. Interactive simulations, educational apps, and online games can provide engaging and personalized learning experiences. However, it's important to choose high-quality resources that align with educational goals and promote conceptual understanding.
Encourage learners to use technology to explore fractions in a dynamic and interactive way. For example, they can use virtual fraction manipulatives to compare fractions, add and subtract fractions, and solve fraction-related problems. However, make sure that technology is used as a supplement to, rather than a replacement for, hands-on activities and conceptual understanding.
6. Address Misconceptions Directly
Be proactive in addressing common misconceptions about fractions. For example, explicitly address the misconception that a larger denominator always means a larger fraction. Use visual models and real-world examples to illustrate that a larger denominator actually means smaller parts.
Provide learners with ample opportunities to identify and correct their own misconceptions. Encourage them to explain their reasoning and justify their answers. By addressing misconceptions directly, you can help learners develop a more accurate and robust understanding of fractions.
FAQ: Understanding Fractions
Q: What is a fraction?
A: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts of the whole you have, and the denominator indicates how many equal parts the whole is divided into.
Q: Why is the denominator important?
A: The denominator determines the size of each fractional part. A larger denominator means the whole is divided into more parts, resulting in smaller individual parts.
Q: How can I compare two fractions?
A: You can compare fractions by finding a common denominator, cross-multiplying, converting to decimals, or using visual aids like pie charts.
Q: What is a common denominator?
A: A common denominator is a denominator that is the same for two or more fractions. Finding a common denominator allows you to directly compare the numerators of the fractions.
Q: What are some common misconceptions about fractions?
A: Common misconceptions include thinking that a larger denominator always means a larger fraction and not understanding improper fractions or mixed numbers.
Conclusion
In summary, understanding fractions is fundamental to mathematical literacy, and comparing fractions accurately is a crucial skill. The statement "1/4 is greater than 1/2" is incorrect because a larger denominator, with the same numerator, indicates smaller parts of a whole. Visual aids, real-world examples, and a solid grasp of the concepts behind numerators and denominators are essential for mastering fractions.
Now that you have a comprehensive understanding of why 1/4 is not greater than 1/2, take the next step in solidifying your knowledge. Practice comparing different fractions and explore real-world applications of fractions to deepen your understanding. Share this article with friends, family, or anyone who might benefit from a clear explanation of this essential mathematical concept, and let's build a stronger foundation in math together!
Latest Posts
Latest Posts
-
How Many Weeks In Ten Years
Nov 28, 2025
-
10 Yards Is How Many Feet
Nov 28, 2025
-
How Many Pounds Is 42 Ounces
Nov 28, 2025
-
Is Melting Ice A Chemical Change
Nov 28, 2025
-
How Many Cups Are 200 Ml
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about Is 1 4 Greater Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.