Is 2 3 Bigger Than 5 6
sandbardeewhy
Nov 27, 2025 · 11 min read
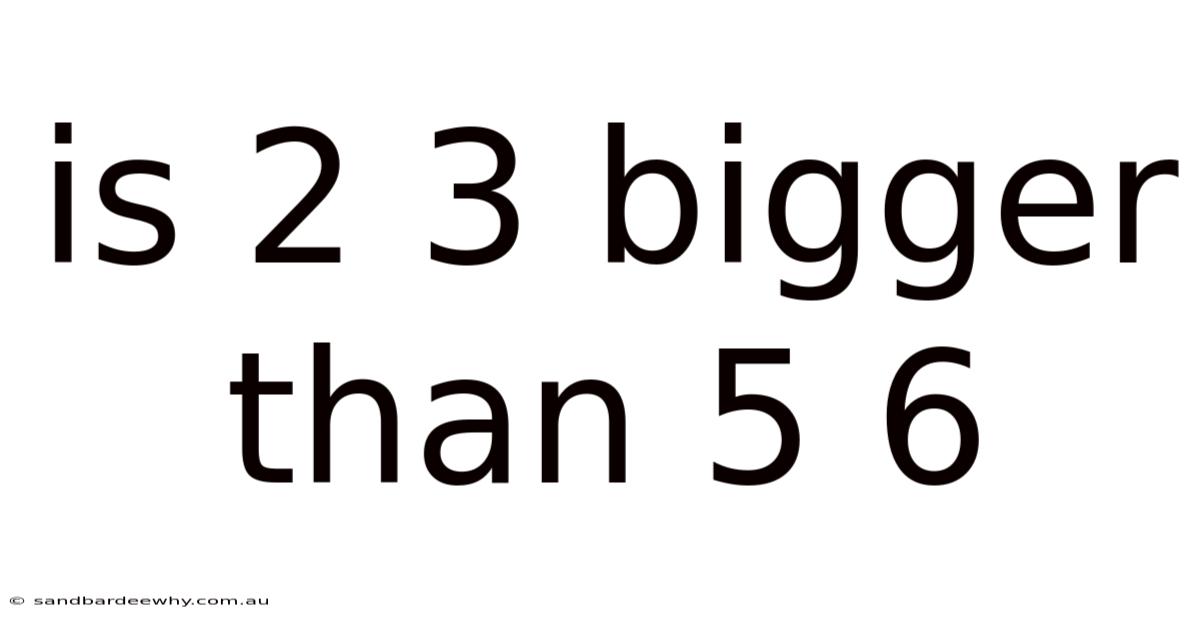
Table of Contents
Imagine you're planning a pizza night with friends. You have two pizzas: one cut into 3 slices and another into 6 slices. You take 2 slices from the first pizza and 5 slices from the second. Do you have more pizza from the first or the second? This simple scenario introduces us to the question: is 2/3 bigger than 5/6? This is a fundamental question of comparing fractions, and understanding it is crucial in various real-world applications, from cooking and budgeting to engineering and finance.
Comparing fractions isn't always straightforward. When the denominators are different, as in the case of 2/3 and 5/6, a direct comparison isn't immediately obvious. To determine which fraction represents a larger quantity, we need to employ a few key strategies. In this comprehensive guide, we'll dive deep into the methods used to compare fractions, explore the underlying mathematical principles, and provide practical examples to ensure you grasp this concept fully. So, let's embark on this mathematical journey and unravel the mystery of whether 2/3 is indeed bigger than 5/6.
Understanding Fractions: A Comprehensive Overview
Fractions are a cornerstone of mathematics, representing parts of a whole. To fully grasp the comparison between 2/3 and 5/6, it's essential to understand the basic components and principles of fractions.
At its core, a fraction consists of two primary components: the numerator and the denominator. The numerator (the top number) indicates how many parts of the whole we have, while the denominator (the bottom number) indicates the total number of equal parts that make up the whole. For instance, in the fraction 2/3, the numerator '2' signifies that we have two parts, and the denominator '3' tells us that the whole is divided into three equal parts. Similarly, in the fraction 5/6, '5' represents the number of parts we have, and '6' represents the total number of equal parts in the whole.
Fractions can be categorized into several types, each with its unique characteristics:
-
Proper Fractions: These are fractions where the numerator is less than the denominator, such as 2/3 or 5/6. Proper fractions always represent a value less than one.
-
Improper Fractions: In these fractions, the numerator is greater than or equal to the denominator, like 7/4 or 9/9. Improper fractions represent a value greater than or equal to one.
-
Mixed Numbers: A mixed number combines a whole number and a proper fraction, such as 1 3/4. Mixed numbers are often used to express improper fractions in a more understandable format. The mixed number 1 3/4 is equivalent to the improper fraction 7/4.
-
Equivalent Fractions: These are fractions that represent the same value, even though they have different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions because they both represent half of a whole.
Understanding these types of fractions and their components is crucial for comparing and manipulating fractions effectively.
The Importance of Common Denominators
When comparing fractions, particularly those with different denominators like 2/3 and 5/6, the concept of a common denominator becomes paramount. A common denominator is a shared multiple of the denominators of the fractions being compared. Using a common denominator allows us to compare the fractions directly by comparing their numerators.
The process of finding a common denominator typically involves identifying the Least Common Multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators. For example, to compare 2/3 and 5/6, we need to find the LCM of 3 and 6. The multiples of 3 are 3, 6, 9, 12, and so on, while the multiples of 6 are 6, 12, 18, 24, and so on. The smallest number that appears in both lists is 6, making it the LCM.
Once we have the common denominator, we need to convert each fraction into an equivalent fraction with the new denominator. To do this, we multiply both the numerator and the denominator of each fraction by a factor that will result in the desired common denominator.
For the fraction 2/3, we multiply both the numerator and the denominator by 2:
(2 * 2) / (3 * 2) = 4/6
The fraction 2/3 is now expressed as the equivalent fraction 4/6.
The fraction 5/6 already has the common denominator of 6, so no conversion is needed.
Now that both fractions have the same denominator, we can easily compare their numerators. The fraction with the larger numerator represents the larger value. In this case, we are comparing 4/6 and 5/6.
Visualizing Fractions
Visual aids can be incredibly helpful in understanding and comparing fractions, especially for those who are new to the concept or find it challenging to grasp abstractly. Visual representations allow us to see the proportional relationships between different fractions, making the comparison more intuitive.
One common method for visualizing fractions is using pie charts or circle diagrams. In this approach, a circle represents the whole, and the fraction is depicted as a slice of the circle. The size of the slice corresponds to the fraction's value. For example, to visualize 2/3, you would divide a circle into three equal parts and shade two of those parts. Similarly, to visualize 5/6, you would divide a circle into six equal parts and shade five of them. By comparing the shaded areas of the two circles, you can visually determine which fraction represents a larger portion of the whole.
Another effective visualization technique is using bar models or rectangles. In this method, a rectangle represents the whole, and the fraction is depicted as a portion of the rectangle. The rectangle is divided into equal parts based on the denominator, and the numerator indicates how many of those parts are shaded. For example, to visualize 2/3, you would divide a rectangle into three equal parts and shade two of those parts. To visualize 5/6, you would divide a rectangle into six equal parts and shade five of them. Again, by comparing the shaded areas, you can visually determine which fraction is larger.
Converting Fractions to Decimals
Converting fractions to decimals is another effective way to compare their values. A decimal is a way of expressing a fraction using the base-10 number system. To convert a fraction to a decimal, you simply divide the numerator by the denominator.
For example, to convert 2/3 to a decimal, you would perform the division 2 ÷ 3. The result is approximately 0.6667 (rounded to four decimal places).
Similarly, to convert 5/6 to a decimal, you would perform the division 5 ÷ 6. The result is approximately 0.8333 (rounded to four decimal places).
Once you have the decimal representations of the fractions, you can easily compare them by comparing their decimal values. The fraction with the larger decimal value is the larger fraction. In this case, 0.8333 is greater than 0.6667, indicating that 5/6 is larger than 2/3.
This method is particularly useful when comparing several fractions or when dealing with fractions that have large or complex denominators. Converting to decimals provides a straightforward and universally comparable format.
Trends and Latest Developments
In recent years, there has been a renewed emphasis on developing innovative and engaging methods for teaching and learning fractions, driven by research in mathematics education and advancements in technology.
Gamification has emerged as a powerful tool for making learning fractions more interactive and enjoyable. Educational games that incorporate fraction concepts, such as comparing fractions, adding fractions, and simplifying fractions, have been shown to improve student engagement and understanding. These games often provide immediate feedback, visual aids, and opportunities for practice, helping students to build a solid foundation in fractions.
Technology has also played a significant role in transforming the way fractions are taught and learned. Interactive simulations, online calculators, and educational apps provide students with opportunities to explore fraction concepts in a dynamic and visual way. These tools can help students to develop a deeper understanding of fractions and their applications in real-world contexts.
Tips and Expert Advice
Comparing fractions can be made easier with a few strategic approaches and a solid understanding of the underlying principles. Here's some expert advice:
-
Simplify Fractions First: Before attempting to compare fractions, always check if they can be simplified. Simplifying fractions involves dividing both the numerator and the denominator by their greatest common factor (GCF). For example, the fraction 4/6 can be simplified by dividing both the numerator and the denominator by 2, resulting in the simplified fraction 2/3. Simplifying fractions makes them easier to work with and can sometimes reveal equivalencies that were not immediately apparent.
-
Cross-Multiplication: Cross-multiplication is a quick and efficient method for comparing two fractions. To use this method, multiply the numerator of the first fraction by the denominator of the second fraction, and then multiply the numerator of the second fraction by the denominator of the first fraction. Compare the two products. The fraction corresponding to the larger product is the larger fraction. For example, to compare 2/3 and 5/6 using cross-multiplication:
- 2 * 6 = 12
- 5 * 3 = 15
Since 15 is greater than 12, 5/6 is greater than 2/3.
-
Benchmark Fractions: Using benchmark fractions like 1/2, 1/4, and 3/4 can provide a quick way to estimate and compare fractions. For example, if you're comparing 3/7 and 5/9, you can recognize that 3/7 is slightly less than 1/2, while 5/9 is slightly more than 1/2. Therefore, 5/9 is larger than 3/7. This method is particularly useful for mental math and quick estimations.
-
Convert to Percentages: Converting fractions to percentages is another way to compare them. To convert a fraction to a percentage, multiply the fraction by 100. For example:
- 2/3 * 100 = 66.67%
- 5/6 * 100 = 83.33%
Comparing the percentages, 83.33% is greater than 66.67%, indicating that 5/6 is larger than 2/3. This method is useful because percentages are often more intuitive and easier to compare than fractions.
-
Practice Regularly: Like any mathematical skill, proficiency in comparing fractions requires practice. Work through a variety of examples, and challenge yourself with increasingly complex problems. Use online resources, textbooks, and worksheets to hone your skills.
FAQ
Q: What is a fraction in its simplest form?
A: A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. For example, 2/3 is in its simplest form, but 4/6 is not because both 4 and 6 are divisible by 2.
Q: How do I find the least common multiple (LCM)?
A: One way to find the LCM is to list the multiples of each number until you find a common multiple. Another way is to use prime factorization. For example, to find the LCM of 3 and 6, you can list the multiples:
- Multiples of 3: 3, 6, 9, 12...
- Multiples of 6: 6, 12, 18, 24...
The LCM is 6.
Q: Can I use a calculator to compare fractions?
A: Yes, most calculators can perform fraction calculations, including comparing fractions. Simply enter the fractions and use the appropriate function to compare them.
Q: What is cross-multiplication, and how does it work?
A: Cross-multiplication is a method for comparing two fractions by multiplying the numerator of each fraction by the denominator of the other fraction. The fraction with the larger product is the larger fraction. For example, to compare a/b and c/d, calculate a * d and b * c. If a * d is greater than b * c, then a/b is greater than c/d.
Q: How do I compare mixed numbers?
A: To compare mixed numbers, first compare the whole number parts. If the whole number parts are different, the mixed number with the larger whole number part is larger. If the whole number parts are the same, compare the fractional parts using any of the methods discussed above.
Conclusion
In summary, to answer the question "is 2/3 bigger than 5/6?" the answer is no, 5/6 is bigger than 2/3. We can use various methods such as finding a common denominator, converting to decimals, or using cross-multiplication to arrive at this conclusion. Understanding these methods not only enhances your mathematical skills but also provides practical tools for everyday situations. Now that you have a solid understanding of comparing fractions, put your knowledge to the test. Try comparing different sets of fractions, explore online resources, and challenge yourself with real-world problems that involve fractions. Continue practicing and refining your skills to master this essential mathematical concept.
Latest Posts
Latest Posts
-
Is Flowers For Algernon A True Story
Nov 27, 2025
-
168 Inches Is How Many Feet
Nov 27, 2025
-
3 4 Is How Many Tablespoons
Nov 27, 2025
-
The Surgical Repair Of A Muscle
Nov 27, 2025
-
What Is Lennie And Georges Dream
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Bigger Than 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.