Least Common Multiple 12 And 9
sandbardeewhy
Nov 22, 2025 · 13 min read
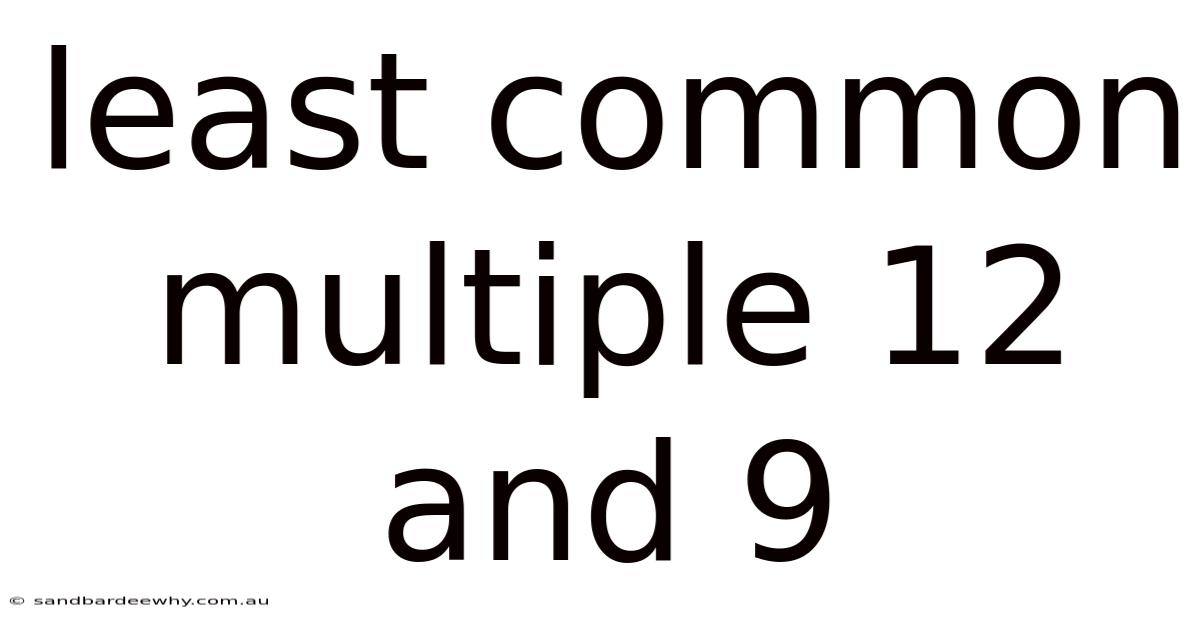
Table of Contents
Have you ever found yourself planning a party, trying to coordinate two different sets of decorations that come in varying quantities? Or perhaps you're a teacher, trying to figure out when two students on different practice schedules will be in the music room simultaneously. These everyday problems, seemingly disparate, share a common mathematical thread: the least common multiple. Understanding the least common multiple, or LCM, isn't just abstract math; it's a practical tool that simplifies many real-world scenarios, making complex arrangements surprisingly straightforward.
Imagine you're baking cookies for a bake sale. One batch requires 12 minutes in the oven, and another needs 9 minutes. If you want to time it perfectly so that both batches finish at the same time, you need to find a common multiple of 12 and 9. The least common multiple helps you discover the shortest time interval at which both batches align. This article will explore the concept of the least common multiple using the example of 12 and 9, offering a comprehensive guide that will equip you with the knowledge to tackle similar problems, whether you're a student, a professional, or just someone who enjoys the elegance of mathematics.
Main Subheading
The least common multiple (LCM) is a foundational concept in number theory with broad applications across various fields of mathematics and beyond. At its core, the LCM of two or more integers is the smallest positive integer that is perfectly divisible by each of those numbers. This means that when you divide the LCM by any of the original numbers, the result is an integer with no remainder. Understanding the LCM helps in simplifying fractions, scheduling events, and solving problems related to cyclical occurrences.
In practical terms, the LCM serves as a tool for identifying the smallest shared interval or quantity between different sets or cycles. Think about coordinating different tasks with varying durations or aligning repeating events that occur at different frequencies. The LCM provides a single point of reference that allows for efficient planning and synchronization. For instance, in music, the LCM can help determine when different rhythmic patterns align; in manufacturing, it can optimize production schedules to minimize waste.
Comprehensive Overview
To fully grasp the significance of the least common multiple, it's essential to delve into its definitions, mathematical foundations, historical context, and practical applications. Understanding these elements will give you a holistic view of why the LCM is such a vital tool.
Definition of Least Common Multiple
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by each of those integers without any remainder. Mathematically, if you have two numbers, a and b, their LCM, denoted as lcm(a, b), is the smallest positive integer m such that a divides m and b divides m.
For example, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, 24, and so on. The multiples of 6 are 6, 12, 18, 24, 30, and so on. The common multiples of 4 and 6 are 12, 24, 36, and so on. The smallest among these common multiples is 12, so the LCM of 4 and 6 is 12.
Scientific Foundations
The concept of the least common multiple is deeply rooted in number theory, a branch of mathematics that deals with the properties and relationships of integers. At the heart of LCM lies the concept of divisibility and factorization. Every integer can be expressed as a product of prime numbers, and understanding these prime factorizations is crucial for finding the LCM.
The fundamental theorem of arithmetic states that every integer greater than 1 can be uniquely expressed as a product of prime numbers, up to the order of the factors. For instance, 12 can be expressed as 2^2 * 3, and 9 can be expressed as 3^2. The LCM is then constructed by taking the highest power of each prime factor that appears in any of the numbers.
History of Least Common Multiple
The historical roots of the least common multiple can be traced back to ancient civilizations, where mathematics was used for practical purposes such as trade, astronomy, and calendar-making. While there is no single inventor of the LCM, the concept was implicitly used in various calculations and problem-solving techniques.
Ancient Babylonian and Egyptian mathematicians dealt with problems involving fractions and proportions, which required an understanding of common multiples. The formal study of number theory, including concepts related to LCM, gained prominence in ancient Greece, with mathematicians like Euclid exploring divisibility and factorization. Euclid's Elements contains algorithms for finding the greatest common divisor (GCD), which is closely related to the LCM.
Essential Concepts Related to LCM
Several related concepts are crucial for a deeper understanding of the least common multiple:
-
Multiples: A multiple of a number is the product of that number and any integer. For example, the multiples of 5 are 5, 10, 15, 20, and so on.
-
Common Multiples: A common multiple of two or more numbers is a number that is a multiple of each of those numbers. For example, common multiples of 4 and 6 are 12, 24, 36, and so on.
-
Greatest Common Divisor (GCD): The greatest common divisor of two or more integers is the largest positive integer that divides each of the integers without any remainder. The GCD and LCM are related by the formula: lcm(a, b) = (a * b) / gcd(a, b)
-
Prime Factorization: The process of expressing a number as a product of its prime factors. For example, the prime factorization of 12 is 2^2 * 3, and the prime factorization of 15 is 3 * 5.
-
Relatively Prime: Two numbers are said to be relatively prime if their greatest common divisor is 1. For example, 8 and 15 are relatively prime because their GCD is 1.
Practical Applications of LCM
The least common multiple finds applications in a wide array of fields:
-
Scheduling: Coordinating events that occur at regular intervals. For example, if one task takes 12 minutes and another takes 9 minutes, the LCM (36) tells you the shortest time interval at which both tasks will finish simultaneously.
-
Fractions: Simplifying fractions by finding a common denominator. For example, to add 1/4 and 1/6, you need to find the LCM of 4 and 6, which is 12. You then rewrite the fractions as 3/12 and 2/12, making it easy to add them.
-
Manufacturing: Optimizing production schedules to minimize waste and maximize efficiency. By aligning different production cycles, manufacturers can reduce downtime and streamline operations.
-
Music: Determining when different rhythmic patterns align. Musicians use LCM to create complex rhythms and harmonies by understanding the relationships between different time signatures.
-
Computer Science: In areas such as cryptography and data synchronization, LCM is used to ensure that processes align correctly and efficiently.
Trends and Latest Developments
In recent years, the concept of the least common multiple has seen a resurgence of interest due to its applications in modern computational algorithms and optimization techniques. As technology advances, efficient methods for calculating LCM are becoming increasingly important in various fields.
One notable trend is the development of more efficient algorithms for computing LCM, especially for large numbers. Traditional methods like prime factorization can become computationally intensive for very large numbers. Researchers have been exploring alternative approaches, such as using binary GCD algorithms, which are faster and more memory-efficient.
Another trend is the integration of LCM concepts into machine learning and data analysis. In certain applications, such as time series analysis and pattern recognition, LCM can be used to identify repeating patterns and synchronize data. For example, in financial markets, LCM can help analyze cycles and predict future trends.
Moreover, the use of LCM in cryptography is gaining attention. Cryptographic algorithms often rely on number theory concepts to ensure security and efficiency. LCM can be used to generate keys and encrypt data in a way that is difficult to crack.
Professional insights suggest that as computational power increases, the applications of LCM will continue to expand. The ability to quickly and accurately compute LCM for large numbers will be crucial in fields such as finance, cybersecurity, and data science.
Tips and Expert Advice
Understanding and applying the least common multiple can be greatly enhanced with practical tips and expert advice. Here are some strategies to effectively use LCM in various scenarios:
-
Master Prime Factorization: Prime factorization is the foundation of finding the LCM. Practice breaking down numbers into their prime factors. For instance, to find the LCM of 12 and 9:
- 12 = 2^2 * 3
- 9 = 3^2
- LCM(12, 9) = 2^2 * 3^2 = 4 * 9 = 36
- The key is to take the highest power of each prime factor present in either number.
- This skill is essential for accurately calculating LCM, especially with larger numbers.
- It provides a systematic approach to finding the smallest common multiple.
-
Use the GCD-LCM Relationship: Remember that lcm(a, b) = (a * b) / gcd(a, b). If you know the greatest common divisor (GCD) of two numbers, you can easily find their LCM. For example, the GCD of 12 and 9 is 3. Therefore:
- LCM(12, 9) = (12 * 9) / 3 = 108 / 3 = 36
- This formula is particularly useful when the GCD is easier to compute than the LCM directly.
- Utilizing this relationship can save time and effort in calculations.
-
List Multiples: For smaller numbers, listing multiples can be a quick way to find the LCM. List the multiples of each number until you find a common multiple.
- Multiples of 12: 12, 24, 36, 48, ...
- Multiples of 9: 9, 18, 27, 36, 45, ...
- The smallest common multiple is 36.
- This method is intuitive and can be particularly effective for numbers that are not too large.
-
Apply LCM to Real-World Problems: Look for opportunities to use LCM in everyday situations. Whether you're scheduling tasks, coordinating events, or simplifying fractions, LCM can provide a solution.
- For example, if you have two tasks, one that repeats every 15 minutes and another every 25 minutes, the LCM (75) tells you that both tasks will align every 75 minutes.
- This skill is invaluable for efficient planning and problem-solving.
- Recognizing these situations helps reinforce your understanding of LCM.
-
Use Technology: There are many online calculators and software tools that can compute the LCM of numbers. These tools can be especially helpful for large numbers or complex problems.
- Tools like Wolfram Alpha or dedicated LCM calculators can provide quick and accurate results.
- However, it's important to understand the underlying principles of LCM rather than relying solely on technology.
- Use technology to verify your manual calculations and explore more complex scenarios.
-
Understand Relatively Prime Numbers: If two numbers are relatively prime (i.e., their GCD is 1), their LCM is simply their product.
- For example, the numbers 8 and 15 are relatively prime.
- Therefore, LCM(8, 15) = 8 * 15 = 120.
- Recognizing relatively prime numbers can simplify LCM calculations.
-
Break Down Complex Problems: When dealing with multiple numbers, break the problem down into smaller steps. Find the LCM of two numbers at a time, and then find the LCM of that result with the next number, and so on.
- For example, to find the LCM of 4, 6, and 9:
- LCM(4, 6) = 12
- LCM(12, 9) = 36
- Therefore, LCM(4, 6, 9) = 36
- This approach makes complex problems more manageable.
- For example, to find the LCM of 4, 6, and 9:
-
Practice Regularly: Like any mathematical skill, proficiency in finding LCM requires regular practice. Work through various problems and examples to reinforce your understanding.
- Use textbooks, online resources, and practice worksheets to test your skills.
- Regular practice builds confidence and improves accuracy.
-
Teach Others: One of the best ways to solidify your understanding of a concept is to teach it to others. Explain the concept of LCM to a friend, family member, or colleague.
- Teaching forces you to organize your thoughts and clarify any misconceptions.
- It also helps you gain a deeper appreciation for the material.
By following these tips and expert advice, you can master the concept of the least common multiple and apply it effectively in various real-world scenarios.
FAQ
Q: What is the least common multiple (LCM)?
A: The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by each of those integers without any remainder. It is the smallest number that is a multiple of all the given numbers.
Q: How do you calculate the LCM of two numbers?
A: There are several methods to calculate the LCM:
- Listing Multiples: List the multiples of each number until you find a common multiple. The smallest common multiple is the LCM.
- Prime Factorization: Find the prime factorization of each number. Then, take the highest power of each prime factor that appears in any of the numbers and multiply them together.
- GCD-LCM Relationship: Use the formula lcm(a, b) = (a * b) / gcd(a, b), where gcd(a, b) is the greatest common divisor of a and b.
Q: What is the relationship between LCM and GCD?
A: The LCM and GCD (greatest common divisor) are related by the formula: lcm(a, b) = (a * b) / gcd(a, b). This means that the LCM of two numbers can be found by dividing the product of the numbers by their GCD.
Q: Why is LCM important?
A: LCM is important for various reasons:
- Simplifying Fractions: It is used to find a common denominator when adding or subtracting fractions.
- Scheduling: It helps in coordinating events that occur at regular intervals.
- Manufacturing: It optimizes production schedules to minimize waste and maximize efficiency.
- Music: It determines when different rhythmic patterns align.
Q: Can LCM be used for more than two numbers?
A: Yes, LCM can be used for more than two numbers. To find the LCM of multiple numbers, you can find the LCM of two numbers at a time, and then find the LCM of that result with the next number, and so on.
Q: What is prime factorization, and how does it relate to LCM?
A: Prime factorization is the process of expressing a number as a product of its prime factors. For example, the prime factorization of 12 is 2^2 * 3. Prime factorization is essential for finding the LCM because it allows you to identify all the prime factors and their highest powers that are needed to form the LCM.
Q: How does LCM apply to real-world problems?
A: LCM has numerous real-world applications:
- Scheduling: Coordinating tasks or events that occur at different intervals (e.g., planning when two buses on different routes will arrive at the same stop).
- Cooking: Adjusting recipes that serve different numbers of people (e.g., scaling up a recipe that serves 4 people to serve 10 people).
- Construction: Aligning repeating patterns in building materials (e.g., determining how many tiles are needed to cover a floor with repeating patterns).
Conclusion
Understanding the least common multiple and its applications can greatly enhance problem-solving skills in various fields. From coordinating events to simplifying fractions, the LCM provides a powerful tool for aligning cycles and optimizing processes. By mastering prime factorization, utilizing the GCD-LCM relationship, and practicing regularly, you can effectively apply LCM in real-world scenarios.
Now that you have a comprehensive understanding of the least common multiple, we encourage you to put your knowledge to the test. Try solving LCM problems, exploring real-world applications, and sharing your insights with others. Engage with our content by leaving comments, asking questions, and suggesting topics for future articles. Your participation will help us create even more valuable resources for the mathematical community.
Latest Posts
Latest Posts
-
What Is 52 Inches In Feet
Nov 22, 2025
-
Study Com Women In Stem Scholarship
Nov 22, 2025
-
Themes Of The Lord Of The Flies
Nov 22, 2025
-
Consider The Lilies Of The Field
Nov 22, 2025
-
The Students Are Going To Listen In Spanish
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple 12 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.