What Is 17 Out Of 20 As A Percentage
sandbardeewhy
Nov 25, 2025 · 12 min read
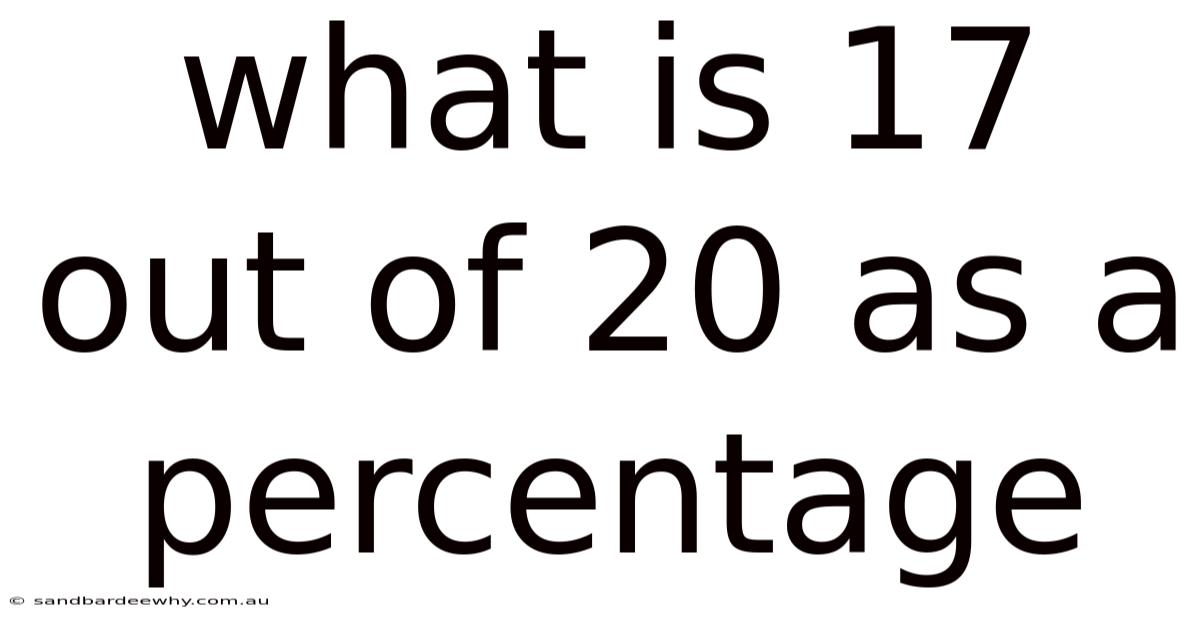
Table of Contents
Imagine you're at a carnival, aiming for the grand prize in a ring toss game. You take 20 shots, and 17 rings land perfectly around the bottles. Excitement rushes through you – you’re so close! But a nagging question pops up: what exactly is your success rate? Figuring out what 17 out of 20 is as a percentage isn’t just about the prize; it's about understanding your performance.
In everyday scenarios, converting fractions into percentages is incredibly useful. Whether it’s calculating your grades, understanding discounts at your favorite store, or even figuring out how well your favorite baseball player is hitting, knowing how to find a percentage helps you make sense of the numbers. This seemingly simple skill provides a clear, standardized way to understand proportions and compare different sets of data. Let's dive into the world of percentages and unlock the mystery behind converting 17/20 into a percentage, making sure you’re always on top of your game.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Essentially, percentages provide a standardized way to understand proportions, making it easy to compare different ratios. For example, saying "50%" means 50 out of every 100, or half of the total.
Percentages are a fundamental concept in mathematics and are used extensively in various fields, including finance, statistics, and everyday life. They allow us to easily grasp proportions and make informed decisions. Whether you're calculating discounts while shopping, understanding interest rates on loans, or analyzing statistical data, percentages are indispensable.
The Mathematical Foundation of Percentages
At its core, a percentage is a ratio or fraction that has been scaled to have a denominator of 100. Mathematically, to convert any fraction to a percentage, you multiply the fraction by 100. This process scales the ratio to a standard base, making it easy to compare different proportions.
The formula to convert a fraction to a percentage is:
Percentage = (Fraction) × 100
For example, if you want to convert the fraction 1/4 to a percentage, you would calculate:
Percentage = (1/4) × 100 = 25%
This indicates that 1/4 is equivalent to 25 out of 100, or 25 percent.
Historical Context and Evolution of Percentages
The concept of percentages dates back to ancient Rome, where calculations were often made in terms of fractions of 100. Roman Emperor Augustus, for example, levied a tax of 1/100 on goods sold at auction, known as centesima rerum venalium. However, the modern concept of percentages as we know it today began to take shape during the Renaissance.
The use of percentages became more widespread with the development of the decimal system and the rise of commerce and finance in Europe during the 15th and 16th centuries. Merchants, bankers, and mathematicians needed a standardized way to express and compare proportions for calculations related to interest, profit, and taxes.
Over time, the notation for percentages evolved as well. While early notations varied, the symbol "%" gradually became standardized, simplifying calculations and communication. The widespread adoption of percentages made financial and statistical analysis more accessible and understandable, contributing significantly to the growth of modern economies.
Essential Concepts Related to Percentages
Several key concepts are closely related to percentages, enhancing their utility in various applications:
-
Base: The base is the total or whole quantity to which the percentage refers. For example, if you say "20% of students," the total number of students is the base.
-
Percentage Increase and Decrease: Percentage increase is the relative increase between two quantities, expressed as a percentage of the original quantity. The formula is:
Percentage Increase = ((New Value - Original Value) / Original Value) × 100
Similarly, percentage decrease is the relative decrease between two quantities, expressed as a percentage of the original quantity. The formula is:
Percentage Decrease = ((Original Value - New Value) / Original Value) × 100
-
Percentage Change: Percentage change is a general term that refers to either percentage increase or percentage decrease. It's used to describe the relative change in a quantity over time.
-
Percentage Points: Percentage points are used to describe the difference between two percentages. For example, if a company's profit margin increases from 10% to 15%, it's an increase of 5 percentage points.
-
Percentage Error: Percentage error is the difference between an estimated value and the actual value, expressed as a percentage of the actual value. It's used to assess the accuracy of estimations or measurements. The formula is:
Percentage Error = ((|Estimated Value - Actual Value|) / Actual Value) × 100
Understanding these concepts enriches the practical application of percentages, allowing for precise analysis and informed decision-making in both professional and personal contexts.
Why Percentages Are Important
Percentages are vital because they simplify the comparison and understanding of proportions. Without percentages, comparing fractions with different denominators can be cumbersome. Percentages provide a common base (100) that makes comparisons straightforward.
Consider the following example: If Company A has a profit of $30 out of $200 revenue, and Company B has a profit of $45 out of $300 revenue, it's difficult to immediately tell which company is more profitable. However, if you convert these figures to percentages:
- Company A Profit Margin = ($30 / $200) × 100 = 15%
- Company B Profit Margin = ($45 / $300) × 100 = 15%
You can quickly see that both companies have the same profit margin of 15%. This ease of comparison is why percentages are so widely used in business, finance, and statistics.
Percentages also facilitate effective communication. People generally understand percentages more easily than fractions or decimals. When presenting data or statistics, using percentages can make the information more accessible and understandable to a broader audience.
Converting 17 out of 20 to a Percentage
Now, let's get back to our original question: what is 17 out of 20 as a percentage? This involves converting the fraction 17/20 into a percentage.
Step-by-Step Conversion
To convert 17/20 to a percentage, you need to follow these steps:
-
Write the fraction: Start with the fraction 17/20.
-
Multiply by 100: Multiply the fraction by 100 to convert it to a percentage.
(17/20) × 100
-
Simplify:
- First, divide 100 by 20, which equals 5.
- Then, multiply 17 by 5.
17 × 5 = 85
-
Add the percent sign: Add the percent sign (%) to the result.
So, 17/20 as a percentage is 85%. This means that 17 out of 20 is equivalent to 85 out of 100.
Alternative Methods for Conversion
There are alternative methods to convert 17/20 to a percentage that can sometimes simplify the calculation:
-
Convert the denominator to 100: Since a percentage is a fraction with a denominator of 100, try to convert the given fraction to have a denominator of 100. To convert 20 to 100, you multiply it by 5. Therefore, multiply both the numerator and denominator by 5:
(17 × 5) / (20 × 5) = 85/100
The fraction 85/100 directly represents 85%.
-
Convert to a decimal first: Divide the numerator by the denominator to convert the fraction to a decimal:
17 ÷ 20 = 0.85
Then, multiply the decimal by 100 to get the percentage:
- 85 × 100 = 85%
Both of these methods provide the same result, offering flexibility depending on your comfort with different mathematical operations.
Real-World Examples
Understanding how to convert fractions to percentages is useful in many real-world scenarios:
- Grading: If you score 17 out of 20 on a quiz, you can quickly calculate your grade as 85%.
- Discounts: If an item is 20% off and originally costs $20, you can calculate the discount amount by finding 20% of 20.
- Statistics: If a survey finds that 17 out of 20 people prefer a certain product, you can report that 85% of the survey respondents prefer that product.
- Finance: If you invest $20 and earn $17 in profit, your return on investment is 85%.
These examples highlight the practical application of percentages in various aspects of daily life, making it easier to interpret and communicate numerical data.
Trends and Latest Developments
The use of percentages continues to evolve with technological advancements and changing societal needs. Here are some current trends and developments:
Data Visualization and Infographics
Percentages are frequently used in data visualization and infographics to present complex information in an accessible format. Visual representations, such as pie charts, bar graphs, and heat maps, often use percentages to highlight proportions and distributions within datasets.
For example, news organizations and research firms use infographics to display survey results, economic data, and demographic trends. By using percentages, they can effectively communicate key findings to a broad audience, regardless of their statistical expertise.
E-commerce and Retail
In e-commerce and retail, percentages are essential for pricing strategies, discounts, and marketing campaigns. Retailers use percentages to calculate markups, margins, and promotional offers. Understanding these percentages helps businesses optimize pricing and maximize profitability.
Dynamic pricing algorithms also rely on percentages to adjust prices in real-time based on demand, competition, and other factors. These algorithms analyze sales data, inventory levels, and market trends to determine the optimal price for each product, often resulting in customized discounts and promotions for individual customers.
Education and Training
Educational platforms and online courses increasingly use interactive tools and simulations to teach percentages and other mathematical concepts. These tools provide students with hands-on experience and immediate feedback, making learning more engaging and effective.
For instance, adaptive learning platforms use algorithms to assess students' understanding of percentages and tailor the content and difficulty level accordingly. This personalized approach helps students master the concept at their own pace, addressing individual learning needs and maximizing outcomes.
Financial Analysis and Investment
Percentages are fundamental to financial analysis and investment decision-making. Investors use percentages to calculate returns on investment, assess risk, and compare the performance of different assets.
Financial analysts also use percentages to evaluate companies' financial statements, calculate key ratios, and forecast future performance. These analyses help investors make informed decisions about buying, selling, or holding stocks, bonds, and other securities.
Professional Insights
As data analytics and business intelligence become more sophisticated, the use of percentages is becoming more nuanced. Professionals are increasingly using percentages in conjunction with other statistical measures to gain a more comprehensive understanding of complex phenomena.
For example, market researchers may use percentages to summarize survey responses, but they also consider confidence intervals, p-values, and other statistical measures to assess the reliability and validity of their findings. This holistic approach helps them draw more accurate conclusions and make better-informed recommendations.
Tips and Expert Advice
Here are some practical tips and expert advice for working with percentages effectively:
Double-Check Your Work
Always double-check your calculations to ensure accuracy. A small error in calculation can lead to significant misinterpretations, especially in financial or statistical analysis. Use a calculator or spreadsheet software to verify your results, particularly when dealing with complex calculations or large datasets.
For example, when calculating a percentage increase or decrease, make sure you use the correct formula and apply it to the appropriate base value. It's also helpful to review your assumptions and input data to identify any potential sources of error.
Understand the Base
Be aware of the base to which the percentage refers. Misunderstanding the base can lead to incorrect conclusions. Always clarify what the percentage is "of" to avoid confusion.
For example, if a company reports a 10% increase in sales, it's essential to know whether this increase is compared to the previous month, the previous quarter, or the previous year. Each of these bases can provide different insights into the company's performance.
Use Benchmarks
Use benchmarks to compare percentages across different contexts. Benchmarks provide a reference point for evaluating performance and identifying areas for improvement.
For example, when assessing a company's profit margin, compare it to the industry average or the profit margins of its competitors. This comparison can help you determine whether the company's performance is above or below par and identify potential opportunities for improvement.
Avoid Percentage Overload
Avoid presenting too many percentages at once, as it can overwhelm your audience. Focus on the most relevant percentages and present them in a clear and concise manner.
When presenting data, use visual aids such as charts and graphs to highlight key percentages and make the information more accessible. Also, provide context and explanations to help your audience understand the significance of the percentages.
Estimate and Approximate
Develop the ability to estimate and approximate percentages mentally. This skill can be useful for quick calculations in everyday situations. Practice estimating percentages of different quantities to improve your mental math skills.
For example, when shopping, estimate the discount amount by approximating the percentage off. If an item is 25% off, quickly estimate the discount by dividing the original price by 4. This can help you make informed purchasing decisions without having to rely on a calculator.
FAQ
Q: What is the formula for converting a fraction to a percentage?
A: The formula is: Percentage = (Fraction) × 100.
Q: How do you convert a percentage back to a fraction?
A: Divide the percentage by 100 and simplify the resulting fraction. For example, 75% = 75/100 = 3/4.
Q: What is the difference between percentage and percentage points?
A: Percentage is a proportion out of 100, while percentage points are the difference between two percentages. For example, if a rate increases from 10% to 12%, it increases by 2 percentage points.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100% if it represents an increase over the original value. For example, if an investment doubles in value, it has increased by 100%, resulting in a final value that is 200% of the original.
Q: How do you calculate percentage increase or decrease?
A: Percentage Increase = ((New Value - Original Value) / Original Value) × 100. Percentage Decrease = ((Original Value - New Value) / Original Value) × 100.
Conclusion
Converting 17 out of 20 to a percentage gives us 85%, a skill that enhances our understanding of proportions in countless scenarios. From calculating grades and discounts to analyzing statistics and financial data, the ability to work with percentages is invaluable. This simple yet powerful tool provides a standardized way to interpret and compare different quantities, making it an essential skill for both personal and professional success.
Now that you've mastered this concept, why not put your knowledge to the test? Explore more complex percentage calculations, analyze real-world data using percentages, or share your newfound expertise with others. Keep practicing and applying this skill, and you'll find yourself making more informed decisions and gaining a deeper understanding of the world around you.
Latest Posts
Latest Posts
-
What Bible Version Do Catholics Use
Nov 25, 2025
-
Law Of Segregation And Independent Assortment
Nov 25, 2025
-
What Is A Product Of Transcription
Nov 25, 2025
-
What Is A 44 Out Of 50
Nov 25, 2025
-
How Much Seconds In A Year
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 17 Out Of 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.