What Is 2 3 Of 16
sandbardeewhy
Nov 28, 2025 · 9 min read
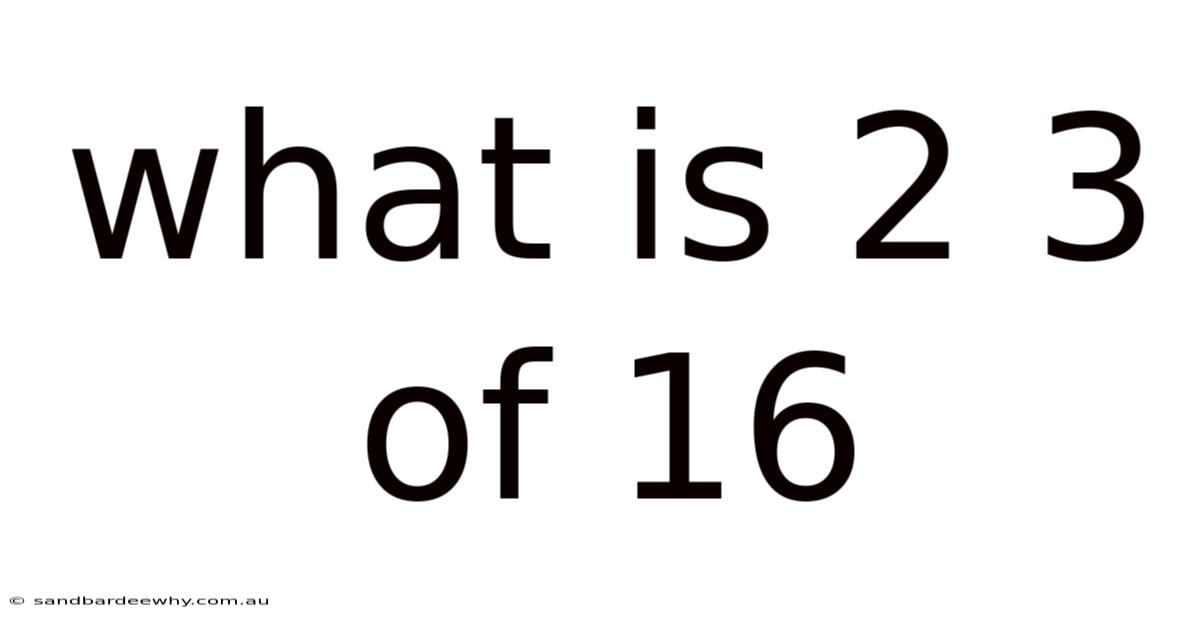
Table of Contents
Imagine you're baking a cake for a party, and the recipe calls for two-thirds of a cup of sugar. But all you have is a measuring cup that holds 16 tablespoons. How many tablespoons do you need to add to get the correct amount? This is a real-life scenario where understanding fractions and their application becomes essential.
Calculating fractions of whole numbers is a fundamental skill applicable far beyond the kitchen. It’s crucial in fields like finance, engineering, and even everyday situations like splitting a bill with friends. Understanding how to find two-thirds of 16 empowers you to solve problems involving proportions and ratios with confidence. Let’s delve into the process and explore its applications.
Main Subheading: Understanding the Basics
To understand what two-thirds of 16 is, it's crucial to break down the concept of fractions. A fraction represents a part of a whole. In the fraction two-thirds (written as 2/3), the number 2 is the numerator, representing the number of parts we're interested in, and the number 3 is the denominator, representing the total number of equal parts the whole is divided into.
When we say "of" in mathematics, it usually indicates multiplication. Therefore, "two-thirds of 16" means 2/3 multiplied by 16. This can be visualized as dividing 16 into three equal parts and then taking two of those parts. The importance of understanding this simple operation extends to various more complex mathematical and real-world applications, laying the foundation for more advanced concepts.
Comprehensive Overview: Deep Dive into Fractions and Multiplication
At its core, finding a fraction of a whole number involves understanding the relationship between fractions, multiplication, and division. Let's break it down step by step.
Definition of a Fraction: A fraction is a numerical quantity that is not a whole number. It represents a part of a whole. As mentioned earlier, it consists of a numerator and a denominator. The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts we are considering. For example, in the fraction 1/4, the whole is divided into four equal parts, and we are considering one of those parts.
Multiplication of a Fraction by a Whole Number: When multiplying a fraction by a whole number, we treat the whole number as a fraction with a denominator of 1. For example, 16 can be written as 16/1. The multiplication then becomes a straightforward process of multiplying the numerators together and the denominators together. So, (2/3) * 16 becomes (2/3) * (16/1).
The Calculation: To calculate two-thirds of 16, we multiply 2/3 by 16/1:
(2/3) * (16/1) = (2 * 16) / (3 * 1) = 32/3
The result is an improper fraction, meaning the numerator is greater than the denominator. To better understand this quantity, we can convert it to a mixed number.
Converting to a Mixed Number: To convert the improper fraction 32/3 to a mixed number, we divide 32 by 3. 32 divided by 3 is 10 with a remainder of 2. Therefore, 32/3 is equal to 10 and 2/3 (written as 10 2/3).
Visual Representation: Imagine you have 16 identical objects, and you need to find two-thirds of them. You would first divide the 16 objects into three equal groups (as much as possible). Since 16 isn't perfectly divisible by 3, you'd get 5 objects in each group, with one object left over. Then, to get two-thirds, you would take two of these groups, which is 10 objects. The remaining object needs to be divided into three parts, and you take two of those parts. Thus, you have 10 whole objects and two-thirds of another object.
Historical Context: The concept of fractions dates back to ancient civilizations. Egyptians and Babylonians used fractions extensively in their calculations for land division, taxation, and construction. The notation and operations with fractions have evolved over centuries, becoming a cornerstone of modern mathematics. Understanding and manipulating fractions is not just a modern mathematical skill; it's a practice with deep historical roots.
Trends and Latest Developments
While the basic principles of calculating fractions remain constant, the way they are taught and applied continues to evolve. Here are some trends and developments:
Emphasis on Conceptual Understanding: Modern mathematics education places a strong emphasis on understanding the "why" behind the calculations, rather than just memorizing formulas. This means using visual aids, real-world examples, and interactive activities to help students grasp the concept of fractions and their applications.
Use of Technology: Technology plays a significant role in teaching and learning about fractions. Interactive simulations, online calculators, and educational apps make it easier for students to visualize fractions and practice calculations. These tools can provide immediate feedback and personalized learning experiences, making the learning process more engaging and effective.
Real-World Applications: Connecting fractions to real-world scenarios is crucial for making the learning relevant and meaningful. Teachers are increasingly using examples from everyday life, such as cooking, budgeting, and sports, to illustrate the use of fractions. This helps students see the practical value of learning about fractions and motivates them to master the skill.
Data Analysis and Statistics: Fractions are fundamental in statistics and data analysis. Calculating percentages, proportions, and probabilities all rely on a solid understanding of fractions. With the increasing importance of data literacy in today's world, a strong foundation in fractions is more critical than ever.
Professional Insight: As a professional, I've observed that individuals with a strong grasp of fundamental math concepts, including fractions, tend to perform better in roles requiring analytical and problem-solving skills. The ability to quickly and accurately calculate fractions is a valuable asset in various fields, from finance to engineering to data science.
Tips and Expert Advice
Here are some practical tips and expert advice to help you master calculating fractions of whole numbers:
Use Visual Aids: Visualizing fractions can make the concept more concrete and easier to understand. Draw diagrams, use fraction bars, or create physical models to represent fractions. This can be especially helpful when learning to add, subtract, multiply, and divide fractions.
For example, if you're trying to find two-thirds of 16, you could draw 16 circles and then try to divide them into three equal groups. This visual representation can help you see that each group would have 5 circles, with one circle left over.
Practice Regularly: Like any skill, mastering fractions requires practice. Work through a variety of problems, starting with simple calculations and gradually moving to more complex ones. Use online resources, textbooks, or worksheets to find practice problems.
Set aside a few minutes each day to practice fraction calculations. Consistency is key to building fluency and confidence.
Break Down Complex Problems: When faced with a complex problem involving fractions, break it down into smaller, more manageable steps. Identify the key information and the operations you need to perform. Work through each step carefully, checking your work as you go.
For example, if you need to calculate two-thirds of 16, you can first find one-third of 16 (which is 16/3) and then multiply that result by 2.
Relate Fractions to Real-World Situations: Connecting fractions to real-world situations can make the learning more engaging and meaningful. Look for opportunities to use fractions in everyday life, such as when cooking, shopping, or measuring.
For example, if you're doubling a recipe that calls for 3/4 cup of flour, you need to multiply 3/4 by 2. This helps you see the practical application of fractions and reinforces your understanding of the concept.
Seek Help When Needed: Don't be afraid to ask for help if you're struggling with fractions. Talk to a teacher, tutor, or friend who is knowledgeable about math. There are also many online resources, such as videos and tutorials, that can provide additional support.
Remember, everyone learns at their own pace. It's okay to ask for help and take your time to master the concept.
FAQ
Q: What does "of" mean in math?
A: In mathematics, "of" often indicates multiplication. When you see "one-half of 10," it means 1/2 multiplied by 10.
Q: How do I multiply a fraction by a whole number?
A: To multiply a fraction by a whole number, treat the whole number as a fraction with a denominator of 1. Then, multiply the numerators together and the denominators together. For example, (1/2) * 5 = (1/2) * (5/1) = (15) / (21) = 5/2.
Q: What is an improper fraction?
A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 5/2 and 7/7 are improper fractions.
Q: How do I convert an improper fraction to a mixed number?
A: To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part. The denominator remains the same. For example, to convert 5/2 to a mixed number, divide 5 by 2. The quotient is 2, and the remainder is 1. Therefore, 5/2 = 2 1/2.
Q: Why is understanding fractions important?
A: Understanding fractions is crucial for many reasons. Fractions are used in everyday life, such as cooking, shopping, and measuring. They are also fundamental in more advanced math concepts, such as algebra, geometry, and calculus. Additionally, fractions are essential in various fields, including finance, engineering, and data science.
Conclusion
In conclusion, finding two-thirds of 16 involves understanding the basic principles of fractions and multiplication. By multiplying 2/3 by 16, we find the result to be 32/3, which can be expressed as the mixed number 10 2/3. This calculation highlights the practical application of fractions in everyday scenarios.
Now that you understand the process, put your knowledge to the test! Try calculating other fractions of whole numbers. Share your results or any questions you have in the comments below. Let's continue to build our mathematical skills together!
Latest Posts
Latest Posts
-
How Do You Use Triple Beam Balance
Nov 28, 2025
-
What Is A Herd Of Camels Called
Nov 28, 2025
-
How Many Tons Is 10000 Pounds
Nov 28, 2025
-
Difference Between Anglican And Catholic Church
Nov 28, 2025
-
Devilfish Island Of The Blue Dolphins
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.