What Is 2 3 Of 20
sandbardeewhy
Nov 26, 2025 · 13 min read
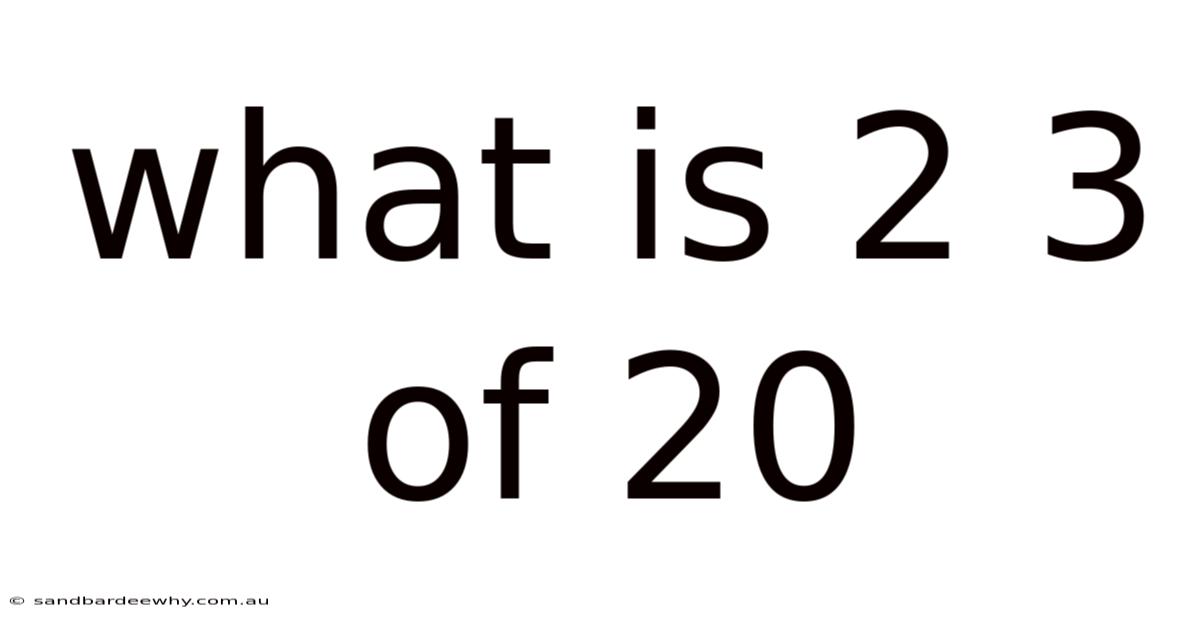
Table of Contents
Imagine you're baking a cake for a party, and the recipe calls for a specific amount of flour. But instead of giving you the exact measurement, it says, "Use 2/3 of a 20-ounce bag." Suddenly, you're faced with a mini math problem right in the middle of your kitchen. Or perhaps you're splitting the cost of a pizza with friends, and your share is 2/3 of the total $20 bill. How much do you owe? These everyday scenarios highlight how understanding fractions and proportions is more than just a classroom exercise; it's a practical skill that helps us navigate the real world.
Calculating fractions of whole numbers is a fundamental concept in mathematics with far-reaching applications. Whether you're figuring out discounts at a store, adjusting quantities in a recipe, or understanding proportions in data, knowing how to find a fraction of a number is essential. In this article, we will explore exactly how to calculate what is 2/3 of 20, and delve into the underlying principles to make this concept clear and applicable to various situations. By the end, you'll not only be able to solve this specific problem but also confidently tackle similar calculations in any context.
Main Subheading: Understanding Fractions and Multiplication
At its core, finding a fraction of a number involves multiplication. A fraction represents a part of a whole, and when we say "2/3 of 20," we're essentially asking: what is two-thirds multiplied by 20? Understanding this relationship is crucial because it transforms the problem into a straightforward multiplication exercise.
Fractions consist of two parts: the numerator and the denominator. The numerator (the top number) tells us how many parts we have, while the denominator (the bottom number) tells us how many parts the whole is divided into. For example, in the fraction 2/3, the numerator 2 indicates that we are interested in two parts, and the denominator 3 indicates that the whole is divided into three equal parts.
The Basic Concept of Multiplying Fractions and Whole Numbers
To find 2/3 of 20, we need to multiply the fraction 2/3 by the whole number 20. A whole number can be expressed as a fraction by placing it over 1. So, 20 becomes 20/1. This transformation is crucial because it allows us to apply the rules of fraction multiplication seamlessly. The rule for multiplying fractions is simple: multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator.
In our case, we multiply 2/3 by 20/1:
- Numerators: 2 * 20 = 40
- Denominators: 3 * 1 = 3
Thus, 2/3 of 20 is equal to 40/3. This fraction can be left as an improper fraction, where the numerator is greater than the denominator, or it can be converted into a mixed number for easier understanding.
Converting Improper Fractions to Mixed Numbers
An improper fraction like 40/3 is not always the most intuitive way to represent a quantity. Converting it into a mixed number provides a clearer sense of its value. A mixed number consists of a whole number and a proper fraction (where the numerator is less than the denominator).
To convert 40/3 into a mixed number, we divide 40 by 3:
- 40 ÷ 3 = 13 with a remainder of 1
The quotient, 13, becomes the whole number part of the mixed number. The remainder, 1, becomes the numerator of the fractional part, and the denominator remains the same (3). Therefore, 40/3 is equal to 13 1/3. This means that 2/3 of 20 is 13 and 1/3.
Practical Examples and Visualizations
Understanding the abstract concept of fractions becomes easier with practical examples and visualizations. Imagine you have a pizza cut into three equal slices, and you want to take two of those slices. That's 2/3 of the pizza. Now, imagine you have 20 cookies, and you want to give away 2/3 of them. This means you're dividing the cookies into three equal groups and giving away two of those groups. To find out how many cookies that is, you calculate 2/3 of 20, which, as we found, is 13 and 1/3 cookies. Since you can't give away a fraction of a cookie, you might round it down to 13 cookies, keeping the remaining cookie pieces for yourself!
Visualizing fractions helps to solidify understanding. For instance, drawing a rectangle and dividing it into three equal parts, then shading two of those parts, visually represents the fraction 2/3. Similarly, drawing 20 individual items and grouping them into three sets can help you see how 2/3 of 20 translates into approximately 13 items.
The Role of Fractions in Everyday Life
Fractions are not confined to textbooks; they are integral to everyday life. Consider cooking, where recipes often require you to double or halve quantities. If a recipe calls for 1/4 cup of sugar and you want to double it, you need to calculate 2 * 1/4, which equals 1/2 cup.
In finance, fractions are used to calculate percentages and proportions. For example, if a store offers a 20% discount on an item, you are essentially calculating 20/100 (or 1/5) of the original price. Understanding fractions allows you to quickly determine the discounted price and make informed purchasing decisions.
In construction and engineering, fractions are used to measure lengths and distances accurately. A carpenter might need to cut a piece of wood to a specific length, such as 3/8 of an inch. Precise calculations are essential to ensure the structural integrity of the project.
Comprehensive Overview: Delving Deeper into Fractions
Now that we've covered the basics of finding a fraction of a number, let's delve deeper into the mathematical foundations and explore different methods for calculating fractions. This will not only reinforce your understanding but also equip you with a variety of tools to tackle more complex problems.
Alternative Methods for Calculating Fractions
While multiplying the fraction by the whole number is the standard method, there are alternative approaches that can be useful in certain situations. One such method involves dividing the whole number by the denominator of the fraction and then multiplying the result by the numerator.
For example, to find 2/3 of 20, you could first divide 20 by 3:
- 20 ÷ 3 = 6.666... (approximately 6.67)
Then, multiply this result by the numerator, which is 2:
- 6.67 * 2 = 13.34 (approximately)
This method yields the same result as the standard multiplication method (13 1/3), albeit with a slight approximation due to rounding. It can be particularly useful when dealing with fractions that have denominators that easily divide into the whole number.
Understanding Decimal Equivalents of Fractions
Another approach involves converting the fraction into its decimal equivalent before performing the multiplication. This can simplify calculations, especially when using a calculator. To convert a fraction to a decimal, you simply divide the numerator by the denominator.
For the fraction 2/3:
- 2 ÷ 3 = 0.666... (approximately 0.67)
Now, multiply this decimal by the whole number:
- 0.67 * 20 = 13.4 (approximately)
Again, this method provides an approximate answer due to rounding. However, it demonstrates the relationship between fractions and decimals and offers another tool for calculating fractions of numbers.
Historical Context of Fractions
The concept of fractions dates back to ancient civilizations. Egyptians used fractions as early as 3000 BC, primarily to solve practical problems related to land division and resource allocation. They had a unique system of representing fractions, mainly using unit fractions (fractions with a numerator of 1).
The Babylonians, on the other hand, used a base-60 number system, which allowed them to express fractions more accurately. Their system was particularly useful for astronomy and navigation, where precise measurements were crucial.
The modern notation for fractions, with a horizontal line separating the numerator and denominator, was introduced by the Arabs. This notation, along with the decimal system, eventually made its way to Europe and revolutionized mathematics and science.
The Importance of Fractions in Advanced Mathematics
Fractions are not just elementary concepts; they are foundational to more advanced topics in mathematics. In algebra, fractions are used extensively to solve equations and manipulate expressions. In calculus, fractions appear in limits, derivatives, and integrals. Understanding fractions is essential for mastering these advanced concepts.
Furthermore, fractions play a crucial role in probability and statistics. Probabilities are often expressed as fractions, representing the likelihood of an event occurring. Statistical analysis often involves calculating proportions and ratios, which are essentially fractions.
Common Misconceptions About Fractions
Despite their widespread use, fractions are often a source of confusion for many students. One common misconception is that the larger the denominator, the larger the fraction. In reality, a larger denominator means that the whole is divided into more parts, making each part smaller. For example, 1/10 is smaller than 1/2.
Another misconception is that fractions must always be less than 1. Improper fractions, where the numerator is greater than the denominator, are perfectly valid fractions. For example, 5/4 is an improper fraction that is greater than 1.
Trends and Latest Developments
In recent years, there has been a renewed emphasis on the importance of mathematical literacy, including a solid understanding of fractions. Educational research has highlighted the need for more effective teaching methods that focus on conceptual understanding rather than rote memorization.
Incorporating Technology in Teaching Fractions
Technology plays an increasingly important role in teaching fractions. Interactive simulations and online tools allow students to visualize fractions and manipulate them in a dynamic way. These tools can help to address common misconceptions and make learning more engaging.
For example, virtual fraction bars allow students to compare different fractions and see how they relate to each other. Online games can make practicing fraction operations more fun and motivating. Adaptive learning platforms can provide personalized feedback and support to students based on their individual needs.
Real-World Data and Statistics Involving Fractions
Real-world data and statistics often involve fractions and proportions. For example, market share data might be expressed as fractions of the total market. Election results might be reported as percentages, which are essentially fractions out of 100.
Understanding how to interpret and analyze data involving fractions is crucial for making informed decisions. Whether you're evaluating investment opportunities, analyzing survey results, or interpreting scientific data, a solid understanding of fractions is essential.
The Use of Fractions in Modern Finance
In modern finance, fractions are used extensively in calculating returns, managing risk, and pricing assets. For example, stock prices are often quoted in fractions of a dollar. Interest rates are expressed as percentages, which are fractions out of 100.
Financial analysts use fractions to calculate ratios and proportions that provide insights into a company's financial performance. These ratios can help investors make informed decisions about whether to buy, sell, or hold a particular stock.
Expert Opinions on the Importance of Fractions
Experts in mathematics education emphasize the importance of developing a strong foundation in fractions. They argue that fractions are not just a topic in elementary school; they are a gateway to more advanced mathematical concepts.
According to Dr. Jo Boaler, a professor of mathematics education at Stanford University, "Fractions are one of the most important building blocks in mathematics. A solid understanding of fractions is essential for success in algebra, calculus, and beyond."
Other experts advocate for a more hands-on, visual approach to teaching fractions. They argue that students should be given opportunities to explore fractions using manipulatives and real-world examples.
Tips and Expert Advice
To master the art of calculating fractions, here are some practical tips and expert advice to help you along the way.
Start with the Basics
Before tackling more complex problems, ensure you have a solid understanding of the basic concepts of fractions. Understand what a fraction represents, how to identify the numerator and denominator, and how to compare different fractions.
Practice converting fractions to decimals and vice versa. Familiarize yourself with common fractions and their decimal equivalents, such as 1/2 = 0.5, 1/4 = 0.25, and 1/3 = 0.333....
Use Visual Aids
Visual aids can be incredibly helpful for understanding fractions. Use fraction bars, pie charts, or number lines to visualize fractions and their relationships.
Draw diagrams to represent fractions and their operations. For example, when adding fractions, draw a rectangle and divide it into the appropriate number of parts to represent each fraction.
Practice Regularly
Like any skill, mastering fractions requires practice. Set aside time each day to work on fraction problems. Start with simple problems and gradually increase the difficulty as you become more confident.
Use online resources, textbooks, and worksheets to find practice problems. Work through the problems step by step, and check your answers to ensure you understand the concepts.
Apply Fractions to Real-World Situations
One of the best ways to understand fractions is to apply them to real-world situations. Look for opportunities to use fractions in your daily life, whether it's cooking, shopping, or managing your finances.
When cooking, double or halve recipes that involve fractions. When shopping, calculate discounts that are expressed as percentages. When managing your finances, track your expenses as fractions of your income.
Seek Help When Needed
If you're struggling with fractions, don't hesitate to seek help from teachers, tutors, or online resources. Ask questions, attend workshops, or join study groups to clarify any concepts you find confusing.
Remember, everyone learns at their own pace. Don't get discouraged if you don't understand something right away. Keep practicing and seeking help, and you'll eventually master fractions.
FAQ
Q: What is a fraction? A: A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number).
Q: How do you multiply a fraction by a whole number? A: Convert the whole number to a fraction by placing it over 1, then multiply the numerators and the denominators.
Q: What is an improper fraction? A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
Q: How do you convert an improper fraction to a mixed number? A: Divide the numerator by the denominator. The quotient is the whole number part, and the remainder is the numerator of the fractional part.
Q: Why are fractions important? A: Fractions are essential for various real-world applications, including cooking, finance, construction, and advanced mathematics.
Conclusion
In summary, calculating 2/3 of 20 involves understanding the fundamental principles of fractions and multiplication. By converting the whole number into a fraction and multiplying the numerators and denominators, we found that 2/3 of 20 is equal to 40/3, which can be expressed as the mixed number 13 1/3. This concept is not just a mathematical exercise; it's a practical skill that helps us solve everyday problems and make informed decisions.
Understanding fractions is crucial for various aspects of life, from cooking and shopping to finance and advanced mathematics. By mastering the basics, practicing regularly, and applying fractions to real-world situations, you can develop a strong foundation in this essential mathematical concept. Now that you understand how to calculate fractions of whole numbers, take the next step and apply this knowledge to real-world problems. Try calculating discounts, adjusting recipes, or analyzing data that involves fractions. Share your experiences and insights with others, and continue to explore the fascinating world of mathematics.
Latest Posts
Latest Posts
-
Fun Facts About The Sioux Tribe
Nov 26, 2025
-
How Can A Nonliving Thing Have An Ecological Footprint
Nov 26, 2025
-
How To Get Angle Of Refraction
Nov 26, 2025
-
How Many Cups Is 300 Grams Sugar
Nov 26, 2025
-
How To Solve For C Using Mvt
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.