What Is 2 Percent Of 40
sandbardeewhy
Nov 27, 2025 · 10 min read
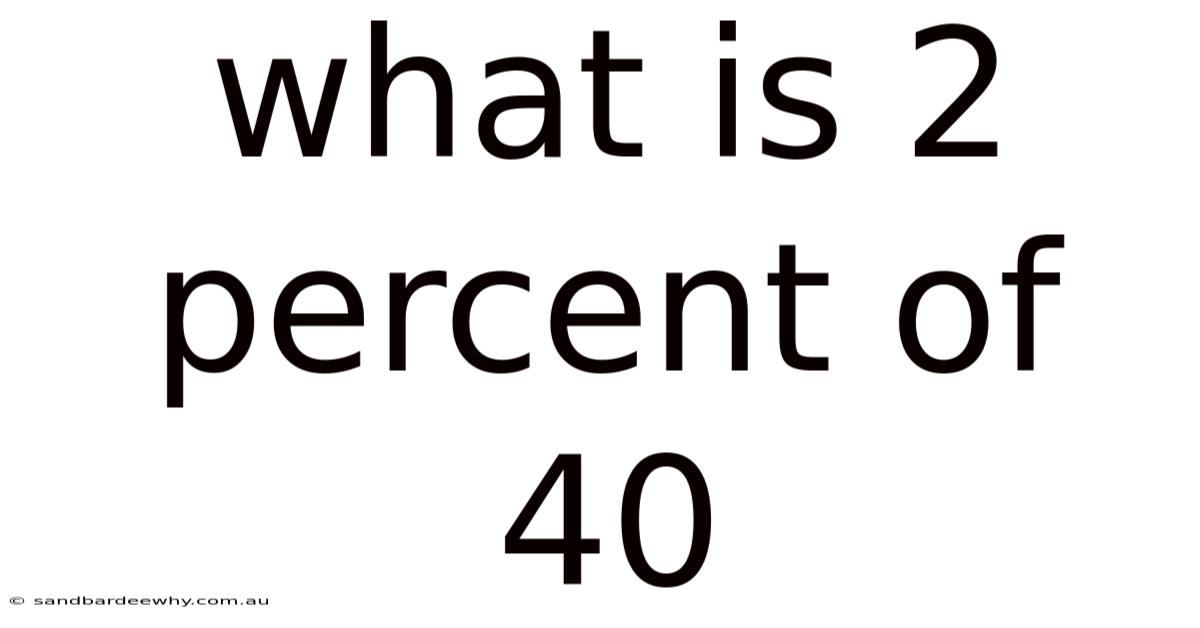
Table of Contents
Have you ever found yourself in a store, eyeing that perfect item, only to be met with a tantalizing discount that requires some quick mental math? Or perhaps you're splitting a bill with friends and need to figure out your share, including a certain percentage for the tip? These everyday scenarios highlight how understanding percentages is a crucial life skill, one that empowers you to make informed decisions and navigate financial situations with confidence.
Percentages might seem like a complex mathematical concept at first glance, but they are actually a straightforward and practical tool. At its core, a percentage is simply a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." So, when we say "2 percent," we're essentially saying "2 out of every 100." This makes percentages incredibly useful for comparing different quantities or understanding proportions, whether it's calculating discounts, analyzing data, or even understanding the nutritional information on a food label.
Main Subheading: Understanding the Basics of Percentages
To fully grasp the concept of percentages, it's essential to understand the underlying principles that make them work. A percentage is a ratio that represents a part of a whole, where the whole is considered to be 100. Think of it like slicing a cake into 100 equal pieces; each piece represents 1 percent of the entire cake. When we calculate a percentage of a number, we are essentially determining what portion of that number corresponds to a specific number of these "slices."
The beauty of percentages lies in their versatility. They provide a standardized way to express proportions, regardless of the original size of the whole. For example, saying that "2 percent of 40" is the same as saying "2 parts out of every 100 parts of 40." This allows us to easily compare proportions across different scales. Whether we're talking about the percentage of students who passed an exam, the percentage of sales growth in a company, or the percentage of body fat in an individual, percentages provide a common language for understanding and interpreting these values.
Comprehensive Overview: Diving Deeper into the World of Percentages
The concept of percentages has a rich history, dating back to ancient Rome. As the Roman Empire expanded, taxes were often levied as a percentage of assets or goods. The Romans used fractions like 1/100 to calculate these taxes, which eventually evolved into the concept of percentages we know today. However, the symbol "%" as we recognize it today didn't appear until much later, in the 15th century. It's believed to have originated from a scribal abbreviation of the Italian word cento, meaning "hundred."
Mathematically, calculating a percentage involves converting the percentage into a decimal or a fraction and then multiplying it by the number you want to find the percentage of. For instance, to find 2 percent of 40, you can convert 2 percent to 0.02 (by dividing 2 by 100) and then multiply 0.02 by 40. Alternatively, you can express 2 percent as the fraction 2/100 and multiply it by 40. Both methods will yield the same result: 0.8. This simple calculation forms the foundation for many real-world applications of percentages.
Percentages are not just confined to simple calculations; they play a vital role in various fields, including finance, statistics, and science. In finance, percentages are used to calculate interest rates, investment returns, and profit margins. In statistics, percentages are used to represent data, compare different groups, and analyze trends. In science, percentages are used to express concentrations, proportions, and errors in measurements. Understanding percentages is crucial for interpreting data, making informed decisions, and communicating information effectively in these fields.
Beyond calculations, it's important to understand the different ways percentages can be used to represent changes in values. For example, a percentage increase represents the relative change in a value from its original amount. If a price increases from $100 to $110, the percentage increase is 10 percent. Conversely, a percentage decrease represents the relative decrease in a value from its original amount. If a price decreases from $100 to $90, the percentage decrease is 10 percent. Understanding these concepts is crucial for interpreting economic data, evaluating investment opportunities, and making informed purchasing decisions.
Another important concept related to percentages is percentage points. Percentage points are used to describe the difference between two percentages. For example, if the unemployment rate increases from 5 percent to 7 percent, the increase is 2 percentage points. It's important to distinguish between percentage points and percentage change. In this example, the percentage change in the unemployment rate is actually 40 percent (calculated as (2/5) * 100), which is significantly different from the 2 percentage point increase. Understanding the difference between these concepts is crucial for accurately interpreting and communicating statistical information.
Trends and Latest Developments: Percentages in the Modern World
In today's data-driven world, percentages are more relevant than ever. They are used extensively in business analytics, market research, and financial modeling. Companies use percentages to track key performance indicators (KPIs), analyze customer behavior, and make data-driven decisions. For example, a retailer might use percentages to track the conversion rate of online shoppers, the click-through rate of email campaigns, or the customer retention rate. These metrics provide valuable insights into the effectiveness of marketing efforts and the overall health of the business.
The use of percentages is also prevalent in political polling and public opinion surveys. Pollsters use percentages to report the level of support for different candidates or policies. These percentages are often accompanied by a margin of error, which represents the range within which the true population value is likely to fall. Understanding the margin of error is crucial for interpreting poll results and avoiding misleading conclusions.
Moreover, with the rise of big data and machine learning, percentages are playing an increasingly important role in data analysis and interpretation. Algorithms often use percentages to represent probabilities, confidence levels, and feature importance. For example, a machine learning model might predict the probability of a customer clicking on an ad with a certain percentage confidence. These percentages help users understand the uncertainty associated with the model's predictions and make more informed decisions.
Furthermore, the way we interact with percentages is also evolving. Interactive dashboards and data visualization tools are making it easier to explore and understand data presented as percentages. These tools allow users to filter data, drill down into specific segments, and visualize trends over time. This interactive approach to data analysis is empowering individuals and organizations to make more informed decisions based on percentage-based insights.
Tips and Expert Advice: Mastering the Art of Percentage Calculations
One of the most effective ways to improve your percentage calculation skills is to practice regularly. Start with simple calculations, such as finding 10 percent, 20 percent, or 50 percent of a number. These percentages are relatively easy to calculate mentally, and they can serve as a foundation for more complex calculations. For example, to find 10 percent of a number, simply move the decimal point one place to the left. To find 50 percent of a number, divide it by 2.
Another useful tip is to break down complex percentage problems into smaller, more manageable steps. For example, if you need to find 17 percent of a number, you can first find 10 percent, then find 5 percent (which is half of 10 percent), and then find 2 percent (which can be calculated directly or derived from 10 percent). By adding these individual percentages together, you can arrive at the final answer. This approach can make even the most challenging percentage problems seem less daunting.
When dealing with percentage increases or decreases, it's important to pay close attention to the base value. The percentage change is always calculated relative to the original value, not the new value. For example, if a price increases from $100 to $120, the percentage increase is 20 percent (calculated as (20/100) * 100). However, if the price then decreases from $120 back to $100, the percentage decrease is not 20 percent. It's actually 16.67 percent (calculated as (20/120) * 100). This difference arises because the base value has changed.
In situations where you need to calculate percentages repeatedly, consider using a spreadsheet program like Microsoft Excel or Google Sheets. These programs have built-in functions for calculating percentages, which can save you time and effort. You can also use these programs to create formulas that automatically update percentages based on changes in the underlying data. This can be particularly useful for tracking financial performance, analyzing sales data, or monitoring key performance indicators.
Finally, don't be afraid to use online percentage calculators to check your work or to solve complex percentage problems. There are many free and reliable percentage calculators available online that can handle a wide range of calculations, including percentage increases, decreases, and differences. These calculators can be a valuable tool for verifying your answers and ensuring accuracy. However, it's important to understand the underlying principles of percentage calculations, even when using a calculator, so that you can interpret the results correctly.
FAQ: Your Questions About Percentages Answered
Q: What is the formula for calculating a percentage? A: The formula for calculating a percentage is: (Part / Whole) * 100.
Q: How do I convert a percentage to a decimal? A: To convert a percentage to a decimal, divide the percentage by 100. For example, 25% = 25/100 = 0.25.
Q: How do I convert a decimal to a percentage? A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 = 0.75 * 100 = 75%.
Q: What is the difference between a percentage increase and a percentage decrease? A: A percentage increase represents the relative increase in a value from its original amount, while a percentage decrease represents the relative decrease in a value from its original amount.
Q: How do I calculate a percentage increase? A: The formula for calculating a percentage increase is: ((New Value - Original Value) / Original Value) * 100.
Q: How do I calculate a percentage decrease? A: The formula for calculating a percentage decrease is: ((Original Value - New Value) / Original Value) * 100.
Q: What are percentage points? A: Percentage points are used to describe the difference between two percentages. For example, if the interest rate increases from 3% to 5%, the increase is 2 percentage points.
Q: How is finding 2 percent of 40 done? A: Convert 2 percent to a decimal (0.02) and multiply by 40: 0.02 * 40 = 0.8.
Conclusion: Mastering Percentages for Everyday Success
Understanding percentages is more than just a mathematical skill; it's a life skill that empowers you to make informed decisions, navigate financial situations with confidence, and interpret data effectively. From calculating discounts at the store to analyzing financial reports at work, percentages are an integral part of our daily lives. By mastering the fundamentals of percentage calculations and practicing regularly, you can unlock a powerful tool for understanding and interpreting the world around you. Remember, to find 2 percent of 40, simply multiply 40 by 0.02, which equals 0.8.
Ready to put your percentage skills to the test? Share this article with your friends and family, and challenge them to solve some percentage problems together. Leave a comment below with your favorite tip for calculating percentages, or share a real-life example of how percentages have helped you make a better decision. Let's continue to learn and grow together in our understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
Fourteen Is 20 Of What Number
Nov 27, 2025
-
How Many Chapters Are In Hatchet
Nov 27, 2025
-
Why Are Least Intrusive Interventions Preferable
Nov 27, 2025
-
Who Was The King Of Troy
Nov 27, 2025
-
Which Of The Following Is Not A Continuous Variable
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.