What Is 2 To The Power Of 4
sandbardeewhy
Nov 28, 2025 · 10 min read
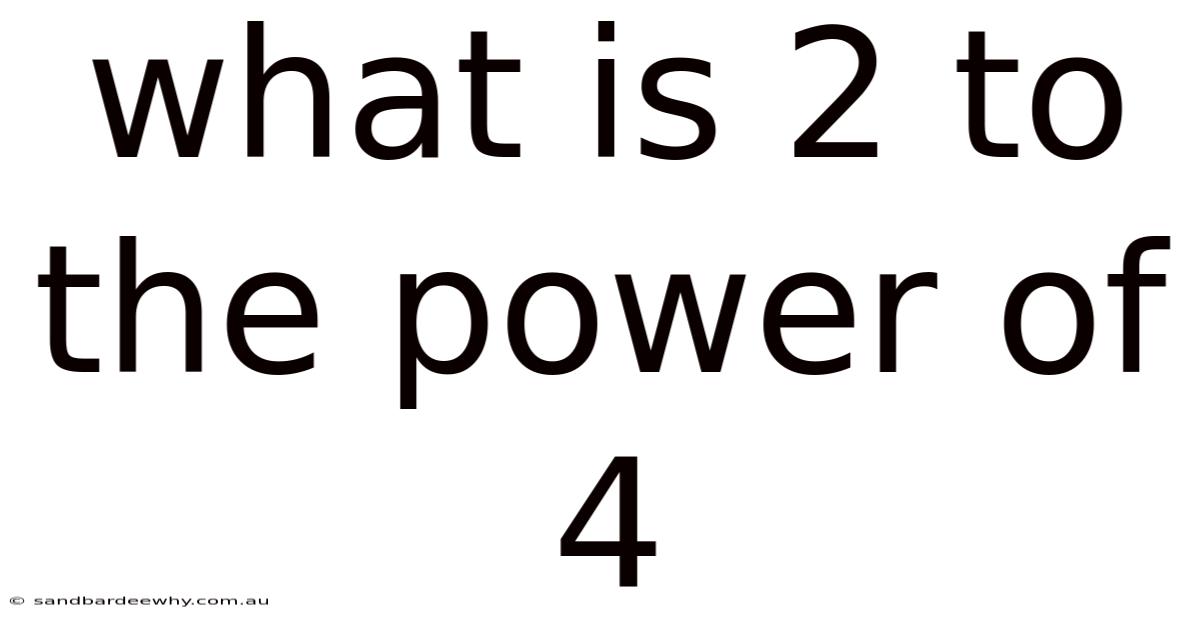
Table of Contents
Imagine you're stacking coins. First, you have one coin. Then you double it, making two. Double that again, and you have four. One more doubling gives you eight, and one final doubling brings you to sixteen shiny coins. This simple act of doubling is the essence of understanding exponents, and in this case, finding out what 2 to the power of 4 is all about.
The concept of exponents might seem intimidating at first, filled with mathematical jargon and abstract symbols. However, at its core, it's simply a shorthand way of expressing repeated multiplication. Instead of writing 2 * 2 * 2 * 2, we can neatly summarize it as 2^4. This expression tells us to multiply the base (2) by itself a specific number of times, indicated by the exponent (4).
Understanding the Basics of Exponents
So, what exactly does it mean when we say "2 to the power of 4"? Let's break it down. The expression 2^4, also written as 2⁴, is read as "2 to the power of 4," "2 raised to the 4th power," or "2 to the fourth." In this expression:
- 2 is the base: The base is the number that is being multiplied by itself.
- 4 is the exponent (or power): The exponent indicates how many times the base is multiplied by itself.
Therefore, 2^4 means multiplying 2 by itself four times: 2 * 2 * 2 * 2.
A Deeper Dive: The Foundation of Exponents
To fully grasp the concept, let's delve into the fundamental principles that underpin exponents:
-
Repeated Multiplication: At its heart, an exponent signifies repeated multiplication. The exponent tells you how many times to use the base as a factor in a multiplication problem.
-
Base and Exponent Relationship: The relationship between the base and exponent is crucial. The base is the number you're multiplying, and the exponent dictates the number of times you multiply it by itself. For instance, in 5³, 5 is the base, and 3 is the exponent, meaning 5 * 5 * 5.
-
Exponential Notation: Exponents provide a concise way to represent repeated multiplication, known as exponential notation. This notation simplifies complex expressions and makes them easier to work with.
-
Reading Exponential Expressions: Understanding how to read exponential expressions is essential. For example, x² is read as "x squared," x³ is read as "x cubed," and x⁴ is read as "x to the fourth power."
-
The Exponent of 1: Any number raised to the power of 1 is simply the number itself. For example, 7¹ = 7. This is because you are only using the base once.
-
The Exponent of 0: Any non-zero number raised to the power of 0 is equal to 1. For example, 10⁰ = 1. This might seem counterintuitive, but it maintains consistency within mathematical rules and patterns.
A Brief History of Exponents
The concept of exponents has evolved over centuries, with contributions from various mathematicians across different cultures. Early notations for exponents were cumbersome and lacked uniformity. Here's a brief look at the history:
-
Ancient Civilizations: The Babylonians and Greeks used repeated multiplication in their calculations, but they didn't have a standardized notation for exponents.
-
Medieval India: Indian mathematicians, such as Brahmagupta, explored concepts related to exponents and negative numbers.
-
16th Century: The use of symbols to represent exponents began to emerge in Europe during the Renaissance. Nicolas Chuquet, a French mathematician, used a notation similar to exponents in his work.
-
17th Century: René Descartes, a French philosopher and mathematician, introduced the modern notation for exponents that we use today in his book La Géométrie (1637).
-
Further Development: Over time, mathematicians developed rules and properties for working with exponents, leading to the formalization of exponentiation as a fundamental mathematical operation.
Core Concepts: Expanding Our Knowledge
Understanding exponents involves grasping several core concepts that extend beyond simple multiplication:
-
Perfect Squares and Cubes: Numbers raised to the power of 2 are known as perfect squares (e.g., 4 = 2²), while numbers raised to the power of 3 are called perfect cubes (e.g., 8 = 2³). Recognizing these patterns can be helpful in various mathematical contexts.
-
Exponential Growth: Exponents are closely related to exponential growth, where quantities increase rapidly over time. This concept is used in fields like finance, biology, and computer science to model phenomena such as population growth, compound interest, and algorithm complexity.
-
Scientific Notation: Exponents play a crucial role in scientific notation, which is used to express very large or very small numbers in a compact and standardized form. For example, the speed of light is approximately 3.0 x 10^8 meters per second.
-
Logarithms: Logarithms are the inverse operation of exponentiation. They are used to find the exponent to which a base must be raised to produce a given number. Logarithms are widely used in fields like physics, engineering, and computer science.
-
Fractional Exponents: Exponents can also be fractions, representing roots. For example, x^(1/2) is the square root of x, and x^(1/3) is the cube root of x. Understanding fractional exponents allows us to work with roots and radicals more easily.
Current Trends and Latest Developments in Exponents
While the fundamental principles of exponents remain unchanged, their applications and interpretations continue to evolve with advancements in technology and mathematical research.
Computational Mathematics
-
High-Performance Computing: Exponents are essential in high-performance computing for tasks like simulating complex systems, modeling physical phenomena, and analyzing large datasets. Efficient algorithms for exponentiation are crucial for optimizing performance in these applications.
-
Cryptography: Exponents play a vital role in modern cryptography, particularly in algorithms like RSA (Rivest–Shamir–Adleman) and Diffie-Hellman key exchange. These algorithms rely on the computational difficulty of certain exponential operations to ensure secure communication and data encryption.
Data Science and Machine Learning
-
Feature Scaling: Exponents are used in feature scaling techniques, such as normalization and standardization, to transform numerical features in datasets. This can improve the performance of machine learning algorithms by ensuring that features have similar ranges of values.
-
Activation Functions: Exponential functions are used in activation functions in neural networks, such as the sigmoid and ReLU (Rectified Linear Unit) functions. These functions introduce non-linearity into neural networks, allowing them to learn complex patterns in data.
Financial Modeling
-
Compound Interest: Exponents are fundamental to calculating compound interest, where interest is earned not only on the principal amount but also on accumulated interest. The formula for compound interest involves raising the interest rate to the power of the number of compounding periods.
-
Option Pricing: Exponents are used in option pricing models, such as the Black-Scholes model, to estimate the fair value of financial options. These models involve exponential functions to account for the time value of money and the probability of future price movements.
Scientific Research
-
Modeling Physical Phenomena: Exponents are used in scientific research to model a wide range of physical phenomena, from radioactive decay to fluid dynamics. Exponential functions can describe how quantities change over time or space.
-
Data Analysis: Exponents are used in data analysis to identify patterns and relationships in experimental data. Exponential curves can be fit to data to model growth rates, decay rates, or other trends.
Expert Insights
-
Optimization: Exponentiation can be computationally expensive, especially for large exponents. Researchers are developing more efficient algorithms for exponentiation, such as exponentiation by squaring, to reduce computational complexity.
-
Quantum Computing: Quantum computers can perform certain exponential operations much faster than classical computers. This has implications for cryptography and other fields where exponents play a key role.
Tips and Expert Advice for Working with Exponents
Understanding exponents is not just about memorizing rules; it's about developing a deep understanding of how they work and how they can be applied in various situations. Here are some practical tips and expert advice to help you master exponents:
-
Master the Basics: Before diving into complex problems, make sure you have a solid understanding of the basic rules of exponents. This includes the product rule, quotient rule, power rule, and negative exponent rule. Practice applying these rules to simple problems until they become second nature.
-
Break Down Complex Problems: When faced with a complex problem involving exponents, break it down into smaller, more manageable steps. Identify the individual operations that need to be performed and apply the appropriate rules of exponents to simplify each step.
-
Use Prime Factorization: Prime factorization can be a powerful tool for simplifying expressions involving exponents. By expressing numbers as products of prime factors, you can often identify common factors that can be canceled out or combined.
-
Watch Out for Negative Signs: Pay close attention to negative signs when working with exponents. Remember that a negative exponent indicates the reciprocal of the base raised to the positive exponent. Also, be careful when raising negative numbers to even or odd powers.
-
Practice Regularly: Like any mathematical skill, mastering exponents requires practice. Set aside time each day or week to work on problems involving exponents. The more you practice, the more comfortable and confident you will become.
-
Use Online Resources: Take advantage of the many online resources available for learning about exponents. Websites like Khan Academy, Wolfram Alpha, and Mathway offer tutorials, practice problems, and step-by-step solutions.
-
Visualize Exponents: Try to visualize exponents to gain a better understanding of how they work. For example, you can think of x² as the area of a square with side length x, and x³ as the volume of a cube with side length x.
-
Real-World Applications: Look for real-world applications of exponents to see how they are used in different fields. This can help you appreciate the power and versatility of exponents.
Frequently Asked Questions (FAQ) about Exponents
-
Q: What is a negative exponent?
- A: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, x^(-n) = 1 / x^n.
-
Q: What is a fractional exponent?
- A: A fractional exponent represents a root. For example, x^(1/2) is the square root of x, and x^(1/3) is the cube root of x.
-
Q: How do I simplify expressions with exponents?
- A: To simplify expressions with exponents, apply the rules of exponents, such as the product rule, quotient rule, and power rule. Combine like terms and cancel out common factors whenever possible.
-
Q: What is the difference between exponentiation and logarithms?
- A: Exponentiation and logarithms are inverse operations. Exponentiation is the process of raising a base to a power, while logarithms are the process of finding the exponent to which a base must be raised to produce a given number.
-
Q: How are exponents used in scientific notation?
- A: Exponents are used in scientific notation to express very large or very small numbers in a compact and standardized form. A number in scientific notation is written as a product of a coefficient between 1 and 10 and a power of 10.
Conclusion
So, what is 2 to the power of 4? It's 16. But more than just a number, it's a gateway to understanding a fundamental mathematical concept with wide-ranging applications. From computer science to finance, exponents are essential tools for modeling and solving problems in the real world. By understanding the basics, exploring advanced concepts, and practicing regularly, you can master exponents and unlock their full potential.
Now that you have a solid grasp of exponents, take the next step. Explore more complex mathematical concepts, apply exponents to real-world problems, and continue to expand your knowledge. Share this article with others who might benefit from it, and leave a comment below to share your own insights and experiences with exponents. What are some of the most interesting or challenging problems you've encountered that involve exponents?
Latest Posts
Latest Posts
-
What Economic System Does The Us Have
Nov 28, 2025
-
20 Oz Is How Many Cups
Nov 28, 2025
-
What Is The Responsibility Of The Secretary Of State
Nov 28, 2025
-
How Long Is The Mackinac Bridge In Miles
Nov 28, 2025
-
How To Find Height From Slant Height
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.