What Is 24 Percent Of 60
sandbardeewhy
Nov 21, 2025 · 10 min read
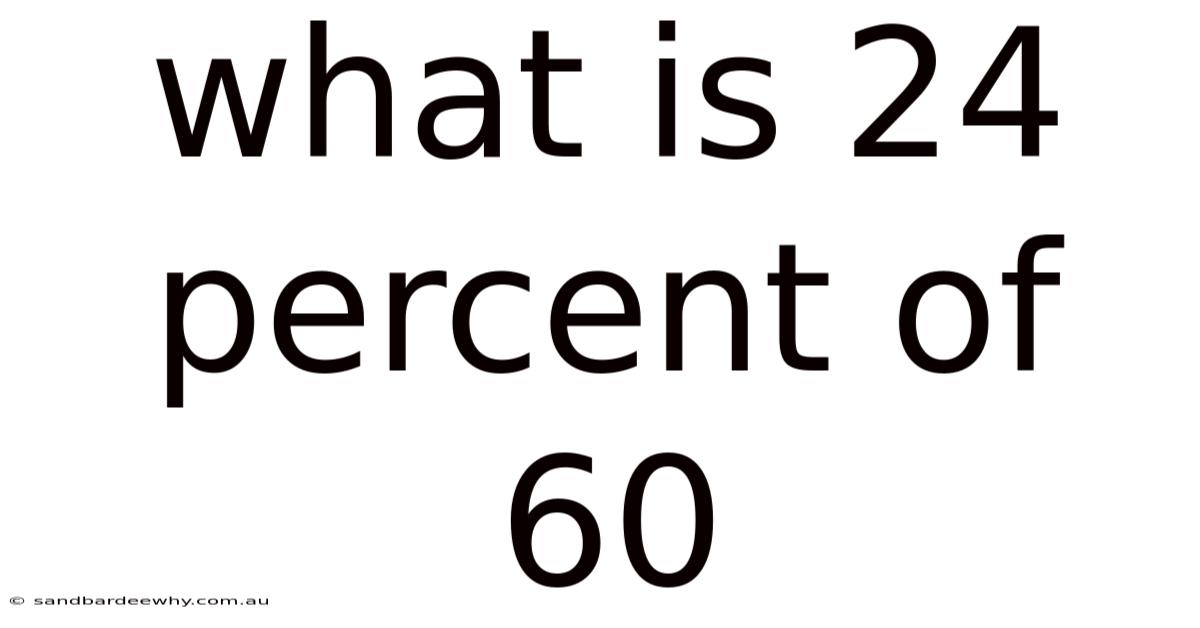
Table of Contents
Imagine you're at a store, and there's a sale offering 24% off on an item priced at $60. Wouldn't you want to quickly figure out how much you're saving? Or picture you’re splitting a bill of $60 with friends, and you're responsible for 24% of it. Knowing how to calculate these percentages swiftly is not just a mathematical exercise; it's a practical life skill.
Whether you’re calculating discounts, figuring out tips, or understanding statistics, the ability to determine a percentage of a number is invaluable. In this article, we'll explore a specific example: finding what 24% of 60 is. We’ll dive into the underlying concepts, different calculation methods, and some handy tips to make this calculation simple and accurate. By the end of this guide, you'll be able to confidently solve similar percentage problems in various real-world scenarios.
Main Subheading: Understanding Percentages
Percentages are an integral part of our daily lives, appearing in financial reports, academic grades, and even in cooking recipes. At its core, a percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, when we say 24 percent, we mean 24 out of every 100.
Understanding percentages requires grasping a few fundamental concepts. First, it's essential to recognize that a percentage is essentially a ratio. For instance, 24% can be written as the fraction 24/100. Second, converting a percentage to a decimal makes calculations easier. To convert a percentage to a decimal, you simply divide it by 100. So, 24% becomes 0.24. With these basics in mind, we can tackle the calculation of what 24% of 60 is, making it a straightforward process.
Comprehensive Overview
Definition of Percentage
A percentage is a way of expressing a number as a fraction of 100. It's a dimensionless number, meaning it doesn't have any units. The symbol "%" is used to denote percentage. In mathematical terms, if you want to express a quantity x as a percentage of a total quantity y, you would calculate (x/y) * 100%. This gives you the proportion of x relative to y in terms of percentage.
Percentages are useful because they provide a standardized way to compare different proportions. For example, if two classes have different numbers of students, comparing the percentage of students who passed an exam gives a clearer picture than comparing the raw numbers. Percentages simplify comparisons and make it easier to understand proportions in various contexts.
The Scientific Foundation of Percentages
The use of percentages is rooted in the mathematical concept of proportions and ratios, which have been used for centuries in various fields. The underlying principle is based on the idea of scaling a ratio to a standard base of 100, making it easier to compare different quantities.
The concept of proportionality, which forms the basis of percentages, is closely related to the mathematical field of ratio and proportion. A ratio expresses the relative size of two quantities, while a proportion states that two ratios are equal. Percentages are simply a standardized way of expressing proportions, making them more intuitive and easier to work with.
Historical Context of Percentages
The concept of percentages can be traced back to ancient Rome, where calculations were often made in terms of fractions of 100. The Romans used a system similar to percentages to calculate taxes, duties, and interest rates. However, the modern concept of percentage as we know it today emerged during the Middle Ages.
During the 15th century, as trade and commerce flourished in Europe, the use of percentages became more widespread. Merchants and traders needed a standardized way to calculate profits, losses, and interest rates. The adoption of the decimal system in the 16th century further facilitated the use of percentages, making calculations easier and more accurate.
Essential Concepts for Calculating Percentages
To calculate what 24 percent of 60 is, it's crucial to understand how to convert percentages to decimals and vice versa. As mentioned earlier, to convert a percentage to a decimal, you divide it by 100. For example, 24% becomes 0.24 when divided by 100. Conversely, to convert a decimal to a percentage, you multiply it by 100. For example, 0.24 becomes 24% when multiplied by 100.
Another essential concept is understanding that "of" in percentage calculations usually means multiplication. Therefore, to find 24% of 60, you need to multiply 0.24 by 60. This simple rule makes calculating percentages straightforward: Percentage of a number = (Percentage as a decimal) * Number.
Methods to Calculate 24 Percent of 60
There are several methods to calculate 24 percent of 60, each offering a different approach to solving the problem. Here are two common methods:
-
Decimal Method:
- Convert the percentage to a decimal: 24% = 0.24
- Multiply the decimal by the number: 0.24 * 60 = 14.4
-
Fraction Method:
- Express the percentage as a fraction: 24% = 24/100
- Multiply the fraction by the number: (24/100) * 60 = (24 * 60) / 100 = 1440 / 100 = 14.4
Both methods yield the same result, providing flexibility in how you approach the calculation. The decimal method is often quicker for those comfortable with decimal multiplication, while the fraction method can be useful for simplifying calculations by reducing fractions.
Trends and Latest Developments
Current Trends in Percentage Usage
Percentages continue to be a fundamental tool in various fields, and their usage is constantly evolving with technological advancements. In finance, percentages are used to calculate interest rates, investment returns, and risk assessments. In retail, they are used to determine discounts, profit margins, and sales growth. In healthcare, percentages are used to analyze patient data, track disease prevalence, and measure treatment effectiveness.
With the rise of big data and data analytics, percentages are becoming even more critical. They provide a standardized way to interpret and communicate complex data sets, making it easier to identify trends, patterns, and insights. Visual tools and dashboards often use percentages to present data in an accessible and understandable format.
Popular Opinions on Percentage Calculations
There are varying opinions on the best methods for calculating percentages, often depending on individual preferences and the specific context. Some people prefer using mental math techniques to quickly estimate percentages, while others rely on calculators or software for precise calculations.
In educational settings, there is an ongoing debate about the importance of teaching manual calculation methods versus relying on technology. While technology can undoubtedly speed up calculations, understanding the underlying principles of percentage calculations is crucial for developing critical thinking and problem-solving skills.
Professional Insights on Percentage Applications
Professionals in various fields emphasize the importance of accuracy and precision when using percentages. In finance, even small errors in percentage calculations can have significant financial implications. In scientific research, accurate percentage calculations are essential for drawing valid conclusions from data.
Experts also highlight the importance of understanding the context in which percentages are used. For example, when interpreting statistical data, it's crucial to consider the sample size and potential biases. Additionally, professionals often use percentages in conjunction with other metrics to gain a more comprehensive understanding of a situation.
Tips and Expert Advice
Simplify Calculations with Mental Math
Mental math can be a powerful tool for quickly estimating percentages, especially in everyday situations. One technique is to break down the percentage into simpler components. For example, to find 24% of 60, you can calculate 20% and 4% separately and then add them together.
- 20% of 60 is (20/100) * 60 = 0.20 * 60 = 12
- 4% of 60 is (4/100) * 60 = 0.04 * 60 = 2.4
- So, 24% of 60 is 12 + 2.4 = 14.4
This approach can make complex percentage calculations more manageable and help you develop a better number sense.
Use Benchmarks for Estimation
Benchmarks are common percentages that are easy to calculate and can be used as reference points for estimating other percentages. Some useful benchmarks include:
- 10% of a number: Divide the number by 10.
- 50% of a number: Divide the number by 2.
- 25% of a number: Divide the number by 4.
- 1% of a number: Divide the number by 100.
For example, to estimate 24% of 60, you can start with 25% of 60, which is 60/4 = 15. Since 24% is slightly less than 25%, the answer will be slightly less than 15. This gives you a quick estimate that you can refine if necessary.
Double-Check Your Work
Accuracy is crucial when calculating percentages, especially in situations where the stakes are high. Always double-check your work to ensure that you haven't made any calculation errors. This is particularly important when dealing with financial calculations or statistical analysis.
One way to double-check your work is to use a different method to calculate the percentage. For example, if you initially used the decimal method, try using the fraction method to verify your answer. Alternatively, you can use a calculator or online tool to confirm your results.
Understand the Context
Percentages can be easily misinterpreted if you don't understand the context in which they are used. Always consider the base number when interpreting percentages. For example, a 10% increase on a small number may be insignificant, while a 10% increase on a large number can be substantial.
Also, be aware of potential biases in the data. For example, if you are analyzing customer satisfaction scores, consider whether the sample is representative of the entire customer base. Understanding the context will help you avoid drawing incorrect conclusions from percentage calculations.
Practice Regularly
Like any skill, calculating percentages becomes easier with practice. Make it a habit to calculate percentages in everyday situations, such as when shopping, dining out, or managing your finances. The more you practice, the more confident and proficient you will become.
You can also use online resources and practice exercises to hone your skills. There are many websites and apps that offer interactive lessons and quizzes on percentage calculations. Regular practice will help you develop a strong number sense and improve your mental math abilities.
FAQ
Q: What is a percentage? A: A percentage is a way of expressing a number as a fraction of 100. It represents a proportion or ratio relative to a whole, where the whole is considered to be 100%.
Q: How do I convert a percentage to a decimal? A: To convert a percentage to a decimal, divide the percentage by 100. For example, 24% becomes 0.24 when divided by 100.
Q: How do I calculate a percentage of a number? A: To calculate a percentage of a number, convert the percentage to a decimal and then multiply the decimal by the number. For example, to find 24% of 60, multiply 0.24 by 60.
Q: Can you explain the decimal method for calculating percentages? A: The decimal method involves converting the percentage to a decimal by dividing it by 100, and then multiplying the decimal by the number you want to find the percentage of. For example, to find 24% of 60, you would convert 24% to 0.24 and then multiply 0.24 by 60, which equals 14.4.
Q: What is the fraction method for calculating percentages? A: The fraction method involves expressing the percentage as a fraction with a denominator of 100, and then multiplying the fraction by the number you want to find the percentage of. For example, to find 24% of 60, you would express 24% as 24/100 and then multiply (24/100) by 60, which equals 14.4.
Conclusion
In summary, calculating 24 percent of 60 involves understanding fundamental concepts of percentages, such as converting percentages to decimals or fractions and applying these conversions to multiplication. Whether you use the decimal method or the fraction method, the key is to accurately apply the mathematical principles involved. Mental math techniques, benchmarks, and regular practice can further enhance your proficiency.
Understanding and calculating percentages is an essential skill applicable in many real-world scenarios. From calculating discounts to understanding statistical data, the ability to work with percentages empowers you to make informed decisions. So, the next time you encounter a percentage problem, remember the methods and tips discussed in this article, and confidently calculate the answer. Why not practice with other numbers or explore more complex scenarios to solidify your understanding?
Latest Posts
Latest Posts
-
What Is The Area Of The Irregular Hexagon
Nov 21, 2025
-
How Many Ounces Is 1 Gal
Nov 21, 2025
-
The Zeroes Of The Function Are
Nov 21, 2025
-
What Is The Basic Foundation Of Neoclassical Literature
Nov 21, 2025
-
How Can You Tell If Someone Is Lying Eyes
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 24 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.