What Is 25 Percent Of 8
sandbardeewhy
Nov 23, 2025 · 12 min read
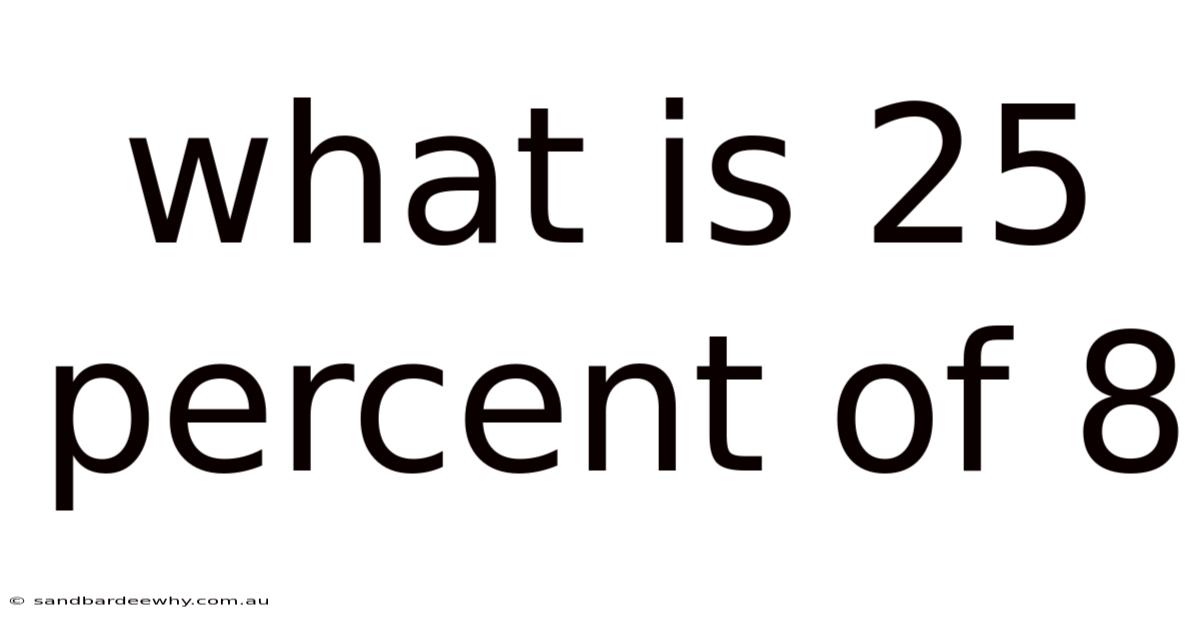
Table of Contents
Have you ever found yourself in a situation where you needed to quickly calculate a percentage of a number? Perhaps you were at a store trying to figure out the sale price of an item, or maybe you were splitting a bill with friends and needed to calculate your share. These everyday scenarios often require us to perform quick mental math, and understanding how to find a percentage of a number is a valuable skill.
Imagine you're out shopping and spot a fantastic gadget priced at $8, but it's advertised with a "25% off" sticker. The excitement of a potential deal is quickly followed by the question: How much will I actually save? This is where knowing how to calculate percentages comes in handy. In this article, we’ll explore a fundamental concept in mathematics: calculating 25 percent of 8, and how it applies to real life.
Unpacking Percentages
Percentages are everywhere, from discounts and taxes to statistics and data analysis. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, a percentage is simply a way of expressing a number as a fraction of 100. This makes it easy to compare proportions and understand relative amounts.
To truly grasp the concept, let's break down the key components. A percentage is a ratio that represents a part of a whole, with the whole being 100%. Think of it as dividing something into 100 equal parts and then looking at how many of those parts you have. For example, if you have 25%, you have 25 out of 100 parts. This can be written as the fraction 25/100 or the decimal 0.25.
Now, let's consider why percentages are so useful. They provide a standardized way to compare different quantities, regardless of their original sizes. Imagine you're comparing two classes: in one class, 10 out of 40 students got an A, and in the other, 15 out of 50 students got an A. Which class performed better? It's not immediately clear, but if you convert these to percentages, you find that 25% of the first class got an A, while 30% of the second class did. This makes the comparison much easier.
Percentages are also essential in finance and economics. Interest rates, inflation rates, and investment returns are all expressed as percentages. Understanding these figures is crucial for making informed financial decisions, whether you're saving for retirement, applying for a loan, or evaluating investment opportunities. Being able to quickly calculate and interpret percentages empowers you to manage your money more effectively.
Furthermore, percentages play a significant role in data analysis and statistics. Researchers use percentages to summarize and present data in a way that is easy to understand. For example, a survey might report that 60% of respondents prefer a certain product. This allows for quick comparisons and helps to identify trends and patterns in the data. In short, mastering percentages is an invaluable skill that can enhance your understanding of the world around you and empower you to make better decisions in various aspects of life.
Comprehensive Overview of Calculating Percentages
The calculation of percentages is rooted in basic arithmetic principles, and understanding these principles is essential for mastering the concept. At its core, finding a percentage of a number involves converting the percentage into a decimal or fraction and then multiplying it by the number. This process allows us to determine what portion of the number the percentage represents.
The scientific foundation behind calculating percentages lies in proportional reasoning. When we say "25 percent of 8," we are essentially asking: "What number is to 8 as 25 is to 100?" This can be expressed as a proportion: x/8 = 25/100. Solving this proportion will give us the answer. To solve for x, we multiply both sides of the equation by 8, resulting in x = (25/100) * 8. This simplifies to x = 0.25 * 8, which equals 2.
Historically, the concept of percentages has evolved alongside the development of mathematics and commerce. Ancient civilizations, such as the Romans, used fractions to calculate taxes and interest rates. However, the modern concept of percentages, with the symbol "%," emerged during the Renaissance period. As trade and finance grew more complex, the need for a standardized way to express proportions became increasingly important. This led to the widespread adoption of percentages as a convenient and universally understood tool for mathematical calculations.
There are several methods you can use to calculate percentages, depending on the context and the tools available to you. One common method is to convert the percentage to a decimal. To do this, divide the percentage by 100. For example, 25% becomes 25/100 = 0.25. Then, multiply the decimal by the number you want to find the percentage of. In our case, 0.25 * 8 = 2.
Another method is to convert the percentage to a fraction in its simplest form. For example, 25% is equivalent to 1/4. Then, multiply the fraction by the number. So, 1/4 * 8 = 2. This method can be particularly useful when dealing with common percentages like 50% (1/2), 25% (1/4), and 75% (3/4).
Additionally, understanding the relationship between fractions, decimals, and percentages is crucial for mastering percentage calculations. Being able to convert fluently between these forms allows you to choose the most efficient method for a given problem. For instance, knowing that 0.5, 1/2, and 50% are all equivalent representations of the same proportion can simplify calculations and make problem-solving easier.
Trends and Latest Developments in Percentage Use
In today's data-driven world, the use of percentages is more prevalent than ever. They are an essential tool for interpreting and communicating information across various fields, from finance and marketing to healthcare and education. Understanding current trends in percentage use can provide valuable insights into how they are applied and perceived in different contexts.
One significant trend is the increasing use of percentages in data visualization. As data sets become larger and more complex, visualizing data in a way that is easy to understand is crucial. Percentages are often used to represent proportions and changes in data, making them a key component of charts, graphs, and infographics. For example, a bar graph might show the percentage of market share held by different companies, or a pie chart might illustrate the distribution of expenses in a budget.
Another trend is the use of percentages in marketing and advertising. Companies often use percentages to highlight discounts, promotions, and savings. However, there is also a growing awareness of the potential for misleading or deceptive use of percentages in advertising. For example, a company might advertise a "50% off" sale, but the original price might be inflated, making the actual savings less significant. As consumers become more savvy, there is an increasing demand for transparency and honesty in percentage-based marketing claims.
In the realm of finance, percentages continue to play a critical role in investment analysis, risk management, and financial planning. Interest rates, return on investment (ROI), and portfolio allocation are all expressed as percentages. Recent developments in financial technology (FinTech) have made it easier for individuals to track and manage their finances using percentage-based tools and metrics. For example, budgeting apps often use percentages to show how much of your income you are spending on different categories.
Furthermore, there is a growing emphasis on statistical literacy and data interpretation in education. As students are exposed to more data in their daily lives, it is essential that they develop the skills to understand and critically evaluate information presented as percentages. This includes understanding the difference between absolute and relative changes, as well as recognizing the potential for bias or misrepresentation in data analysis.
Professional insights suggest that the effective use of percentages requires not only mathematical proficiency but also contextual awareness and critical thinking skills. When interpreting percentages, it is important to consider the sample size, the margin of error, and any potential confounding factors that might influence the results. It is also important to be aware of the limitations of percentages and to use them in conjunction with other forms of data and analysis.
Tips and Expert Advice on Percentage Calculations
Calculating percentages accurately and efficiently can be a valuable skill in many aspects of life. Whether you're shopping, managing your finances, or analyzing data, mastering percentage calculations can help you make informed decisions and solve problems more effectively. Here are some tips and expert advice to enhance your understanding and proficiency in working with percentages.
First, understand the basics. Make sure you have a solid grasp of the fundamental concepts of percentages, fractions, and decimals. This includes knowing how to convert between these forms and understanding the relationship between them. For example, knowing that 25% is equivalent to 0.25 and 1/4 can help you choose the most efficient method for a given calculation.
Next, use benchmarks. Familiarize yourself with common percentages like 10%, 25%, 50%, and 75%. These benchmarks can serve as mental shortcuts for quick calculations. For example, if you need to calculate 10% of a number, simply move the decimal point one place to the left. To find 20%, double the result of 10%. These mental strategies can save time and reduce the risk of errors.
Another tip is to break down complex problems. When dealing with more complex percentage calculations, break the problem down into smaller, more manageable steps. For example, if you need to calculate a discount of 15% followed by a sales tax of 8%, calculate the discount first and then apply the sales tax to the reduced price. This step-by-step approach can help you avoid confusion and ensure accuracy.
Use estimation to check your work. Before performing a percentage calculation, take a moment to estimate the answer. This can help you catch errors and ensure that your final answer is reasonable. For example, if you're calculating 25% of 8, you know that the answer should be less than 8 but more than 0. If your calculation yields an answer outside of this range, it's a sign that you may have made a mistake.
Practice regularly. Like any skill, proficiency in percentage calculations requires practice. Incorporate percentage calculations into your daily routine, whether you're calculating discounts while shopping, tracking your expenses, or analyzing data at work. The more you practice, the more confident and accurate you will become.
Finally, leverage technology. Take advantage of calculators, spreadsheets, and online tools to simplify percentage calculations. These tools can save time and reduce the risk of errors, especially when dealing with complex or repetitive calculations. However, it's important to understand the underlying principles and not rely solely on technology, as this can limit your ability to solve problems in situations where technology is not available.
FAQ About Percentages
Q: What does "percent" mean? A: "Percent" means "out of one hundred." It is a way of expressing a number as a fraction of 100, denoted by the symbol "%."
Q: How do I convert a percentage to a decimal? A: To convert a percentage to a decimal, divide the percentage by 100. For example, 25% = 25/100 = 0.25.
Q: How do I convert a decimal to a percentage? A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 = 0.75 * 100 = 75%.
Q: How do I calculate the percentage of a number? A: To calculate the percentage of a number, convert the percentage to a decimal or fraction and then multiply it by the number. For example, to find 25% of 8, multiply 0.25 by 8, which equals 2.
Q: What is the formula for calculating percentage increase or decrease? A: The formula for calculating percentage increase or decrease is: ((New Value - Old Value) / Old Value) * 100. A positive result indicates an increase, while a negative result indicates a decrease.
Q: How can percentages be used in real-life scenarios? A: Percentages are used in many real-life scenarios, such as calculating discounts while shopping, managing personal finances, analyzing statistical data, and understanding economic indicators.
Q: What is the difference between percentage and percentage points? A: Percentage and percentage points are related but different concepts. A percentage is a ratio expressed as a fraction of 100, while a percentage point is the arithmetic difference between two percentages. For example, if an interest rate increases from 5% to 7%, it has increased by 2 percentage points.
Q: Are there common mistakes to avoid when working with percentages? A: Yes, common mistakes include confusing percentages with percentage points, not converting percentages to decimals or fractions before performing calculations, and misunderstanding the base value when calculating percentage change.
Q: How do I calculate the original price after a discount? A: To calculate the original price after a discount, divide the sale price by (1 - discount percentage). For example, if an item is sold for $60 after a 20% discount, the original price is $60 / (1 - 0.20) = $75.
Q: Can I use a calculator to calculate percentages? A: Yes, calculators and online tools can simplify percentage calculations, especially for complex or repetitive tasks. However, it's important to understand the underlying principles and not rely solely on technology.
Conclusion
In conclusion, calculating 25 percent of 8 is a fundamental mathematical operation with practical applications in everyday life. By understanding the basic principles of percentages, you can easily determine that 25% of 8 is 2. This calculation involves converting the percentage into a decimal (0.25) and then multiplying it by the number (8). The result, 2, represents the portion of 8 that corresponds to 25%.
Throughout this article, we've explored the concept of percentages, their historical roots, and their relevance in various fields, from finance to marketing. We've also discussed current trends in percentage use, such as data visualization and statistical literacy. In addition, we've provided practical tips and expert advice to enhance your understanding and proficiency in working with percentages.
Now that you have a comprehensive understanding of calculating 25 percent of 8 and percentages in general, we encourage you to put your knowledge into practice. Whether you're shopping, managing your finances, or analyzing data, use your newfound skills to make informed decisions and solve problems more effectively. Share this article with your friends or colleagues who might benefit from this information. Don't hesitate to explore additional resources and continue learning about the fascinating world of mathematics.
Latest Posts
Latest Posts
-
How To Say To Look For In Spanish
Nov 23, 2025
-
What Is Half Of 1 And 1 4 Cup
Nov 23, 2025
-
How Many Pounds Are In 32 Oz
Nov 23, 2025
-
What Is Answer To Multiplication Problem Called
Nov 23, 2025
-
How To Finalize A Ppt Presentation
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.