What Is The Decimal Of 1/10
sandbardeewhy
Nov 23, 2025 · 10 min read
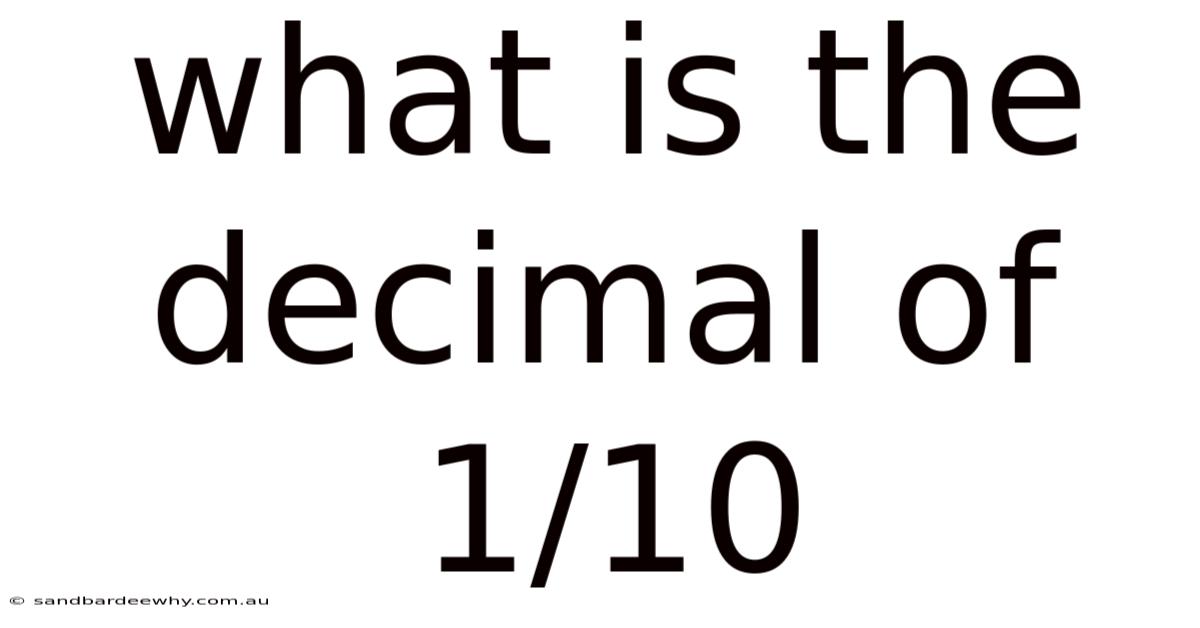
Table of Contents
The aroma of freshly brewed coffee filled the air as Sarah, a budding entrepreneur, meticulously reviewed her business plan. Every detail mattered, from projected revenue to marketing strategies. Yet, she found herself momentarily stumped by a seemingly simple calculation: What is the decimal equivalent of 1/10? It felt like a basic math problem from her school days, but in the high-stakes world of business, accuracy was paramount.
Similarly, consider a chef perfecting a new recipe. A slight miscalculation in the proportion of ingredients can alter the entire flavor profile. The difference between success and failure often lies in the precision of measurements, and understanding basic mathematical concepts like converting fractions to decimals is crucial. For both Sarah and the chef, the decimal representation of 1/10 isn't just a number; it's a foundational element of their respective crafts. In this comprehensive guide, we will explore the decimal representation of 1/10, its significance, and its practical applications across various fields.
Main Subheading: Understanding Fractions and Decimals
Fractions and decimals are two different ways of representing numbers that are less than one whole unit. Fractions, like 1/10, represent a part of a whole, while decimals use a base-10 system to express these parts. Converting between fractions and decimals is a fundamental skill in mathematics and is widely used in everyday life, from calculating percentages to measuring ingredients in a recipe.
Understanding the relationship between fractions and decimals begins with grasping the concept of place value. In the decimal system, each digit to the right of the decimal point represents a fraction with a denominator that is a power of 10. For example, the first digit after the decimal point represents tenths, the second represents hundredths, the third represents thousandths, and so on. This system allows for precise representation of numbers that fall between whole numbers.
Comprehensive Overview: Diving Deep into 1/10
The fraction 1/10 (one-tenth) is a common and straightforward example of a fraction that represents a part of a whole. The number "1" (numerator) indicates the number of parts we have, and the number "10" (denominator) indicates the total number of equal parts into which the whole is divided. To understand its decimal representation, it's essential to break down the underlying mathematical principles.
The Basic Definition
At its core, 1/10 signifies one part out of ten equal parts. Visualize a pie cut into ten equal slices; 1/10 represents one of those slices. This simple fraction is a cornerstone in understanding proportions, ratios, and percentages. It is also the foundation of the decimal system itself, where each position to the right of the decimal point signifies a power of ten.
Converting 1/10 to Decimal Form
To convert a fraction to a decimal, you divide the numerator (the top number) by the denominator (the bottom number). In the case of 1/10, you divide 1 by 10.
Mathematically, this is expressed as:
1 ÷ 10 = 0.1
The result, 0.1, is the decimal representation of 1/10. The "0" to the left of the decimal point indicates there are no whole units, and the "1" to the right of the decimal point indicates one-tenth.
Understanding Place Value
In the decimal system, the position of a digit relative to the decimal point determines its value. The first position to the right of the decimal point is the tenths place, the second is the hundredths place, the third is the thousandths place, and so on.
Therefore, in the decimal 0.1:
- The "0" is in the ones place (representing 0 whole units).
- The "1" is in the tenths place (representing 1/10).
Visual Representation
Visual aids can further clarify the concept. Imagine a number line stretching from 0 to 1. If you divide this line into ten equal segments, the first segment marks the point 0.1, which is the decimal equivalent of 1/10. Similarly, a pie chart divided into ten equal segments would visually represent 1/10 as one of those segments, emphasizing its proportional relationship to the whole.
Historical Context
The concept of fractions and decimals has ancient roots. Fractions were used by ancient Egyptians and Babylonians, while the decimal system, as we know it today, evolved over centuries. The decimal system's widespread adoption facilitated trade, scientific calculations, and engineering by providing a standardized way to represent and manipulate numbers. The decimal representation of 1/10, therefore, is not just a mathematical value but also a product of historical mathematical evolution.
Trends and Latest Developments
In modern mathematics, the decimal representation of 1/10 continues to be fundamental, especially in the context of computer science, data analysis, and financial modeling. The advent of high-precision computing has only amplified the importance of accurate decimal representations in complex calculations.
Data Science and Machine Learning
In data science, datasets often involve fractional values that need to be processed efficiently. Machine learning algorithms rely on numerical data, and the accurate conversion and representation of fractions as decimals are crucial for training models. For instance, in feature scaling, values are often normalized to a range between 0 and 1, requiring precise decimal representations like 0.1.
Financial Technology (FinTech)
In FinTech, transactions often involve fractional amounts, such as interest rates or stock prices. Decimal accuracy is paramount to ensure fair and precise financial operations. Financial software and algorithms must handle decimal representations of fractions, like 1/10, with utmost precision to avoid errors that could have significant financial implications.
Scientific Research
Scientific research frequently involves measurements and calculations that require high precision. Instruments often provide readings in decimal format, and researchers rely on these values to conduct experiments and analyze data. The decimal representation of simple fractions like 1/10 serves as a building block for more complex scientific calculations.
Popular Opinion and Misconceptions
Despite its simplicity, there are common misconceptions about decimal representations. Some people may confuse 0.1 with other similar decimals, such as 0.01 (one-hundredth) or 0.11 (eleven-hundredths). It’s crucial to emphasize the place value concept to avoid such misunderstandings. Educational resources often use visual aids and interactive tools to reinforce the correct understanding of decimal values.
Professional Insights
From a professional standpoint, understanding decimal representations is not merely an academic exercise but a practical necessity. Engineers, scientists, financiers, and even chefs rely on this knowledge to perform their jobs effectively. Continuous education and training often include refresher courses on basic mathematical concepts to ensure professionals maintain a high level of accuracy in their work.
Tips and Expert Advice
Mastering the conversion of fractions to decimals can greatly enhance one's mathematical proficiency. Here are some practical tips and expert advice to help you understand and apply this concept effectively.
Tip 1: Practice Regularly
Like any skill, converting fractions to decimals requires consistent practice. Start with simple fractions like 1/2, 1/4, and 1/5 and gradually move to more complex fractions. Use online resources, worksheets, and interactive exercises to reinforce your understanding. Regular practice builds confidence and helps you quickly recall decimal equivalents.
For example, try converting fractions like 3/4, 2/5, and 7/10 to decimals. Check your answers using a calculator to ensure accuracy. Over time, you will develop an intuitive sense for converting common fractions to their decimal representations.
Tip 2: Use Visual Aids
Visual aids can be particularly helpful for understanding the concept of fractions and decimals. Draw diagrams, use pie charts, or visualize number lines to represent fractions and their decimal equivalents. These visual representations can make abstract concepts more concrete and easier to grasp.
For instance, if you're struggling to understand 1/10 as 0.1, draw a rectangle and divide it into ten equal parts. Shade one of those parts to represent 1/10. This visual representation helps you see the proportional relationship between the fraction and its decimal equivalent.
Tip 3: Memorize Common Conversions
Memorizing the decimal equivalents of common fractions can save you time and effort in many situations. Fractions like 1/2 (0.5), 1/4 (0.25), 1/5 (0.2), 1/10 (0.1), and 1/3 (0.333...) appear frequently in everyday calculations. Knowing these conversions by heart can speed up your problem-solving process.
Create flashcards or use mnemonic devices to help you memorize these common conversions. Regularly test yourself to reinforce your memory. Over time, these conversions will become second nature.
Tip 4: Understand the Relationship Between Fractions and Percentages
Fractions, decimals, and percentages are closely related. Understanding this relationship can make it easier to convert between these forms. To convert a decimal to a percentage, multiply it by 100. For example, 0.1 (which is the decimal form of 1/10) multiplied by 100 equals 10%, so 1/10 is equivalent to 10%.
Similarly, to convert a percentage to a decimal, divide it by 100. For example, 25% divided by 100 equals 0.25, which is the decimal form of 1/4. Understanding these conversions can help you solve a wide range of problems involving proportions and ratios.
Tip 5: Use Technology Wisely
While it’s important to understand the underlying concepts, technology can be a valuable tool for converting fractions to decimals. Calculators, online converters, and smartphone apps can quickly and accurately perform these conversions. However, avoid relying solely on technology without understanding the math behind it.
Use technology to check your work and to explore more complex conversions. For example, you can use a calculator to convert fractions like 17/23 or 41/59 to decimals. However, make sure you also understand the process of dividing the numerator by the denominator to arrive at the decimal equivalent.
Expert Advice: Emphasize Conceptual Understanding
The most important piece of advice is to emphasize conceptual understanding over rote memorization. Instead of simply memorizing conversions, strive to understand why those conversions work. Focus on the relationship between fractions, decimals, and place value. This deeper understanding will enable you to solve a wider range of problems and to apply your knowledge in new and creative ways.
For example, when converting 1/10 to 0.1, understand that 1/10 represents one part out of ten, and 0.1 represents one-tenth in the decimal system. This conceptual understanding will help you generalize your knowledge to other fractions and decimals.
FAQ: Frequently Asked Questions
Q: What is the decimal of 1/10?
A: The decimal representation of 1/10 is 0.1. This means one-tenth.
Q: How do you convert 1/10 to a decimal?
A: To convert 1/10 to a decimal, divide the numerator (1) by the denominator (10). 1 ÷ 10 = 0.1.
Q: Why is it important to know the decimal equivalent of 1/10?
A: Knowing the decimal equivalent of 1/10 is important because it's a fundamental concept in mathematics and is used in various real-world applications, such as finance, science, and everyday calculations.
Q: Can you provide other examples of converting fractions to decimals?
A: Certainly! For example, 1/4 is equal to 0.25, and 1/2 is equal to 0.5. To convert these, you divide 1 by 4 and 1 by 2, respectively.
Q: How does place value relate to the decimal representation of 1/10?
A: In the decimal 0.1, the "1" is in the tenths place, meaning it represents one-tenth. The decimal system is based on powers of 10, so each position to the right of the decimal point represents a fraction with a denominator that is a power of 10.
Conclusion
In summary, the decimal representation of 1/10 is 0.1, a fundamental concept with wide-ranging applications. Understanding this conversion requires grasping the relationship between fractions and decimals, the significance of place value, and the practical methods for converting between these forms. Whether you're a student, a professional, or simply someone looking to enhance your mathematical literacy, mastering the decimal equivalent of 1/10 is a valuable skill.
Now that you have a comprehensive understanding of the decimal representation of 1/10, put your knowledge to the test! Try converting other fractions to decimals and explore how these concepts apply in your everyday life. Share your findings and any additional tips in the comments below, and let's continue learning together.
Latest Posts
Latest Posts
-
How Many Feet Is 14 Meters
Nov 23, 2025
-
What Is Jupiter The God Of
Nov 23, 2025
-
How Many Pounds Is 67 Kilograms
Nov 23, 2025
-
How Many Pounds Is 8 Tons
Nov 23, 2025
-
6 Cups Is How Many Quarts
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Is The Decimal Of 1/10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.