What Is The Decimal Of 1 3
sandbardeewhy
Nov 25, 2025 · 11 min read
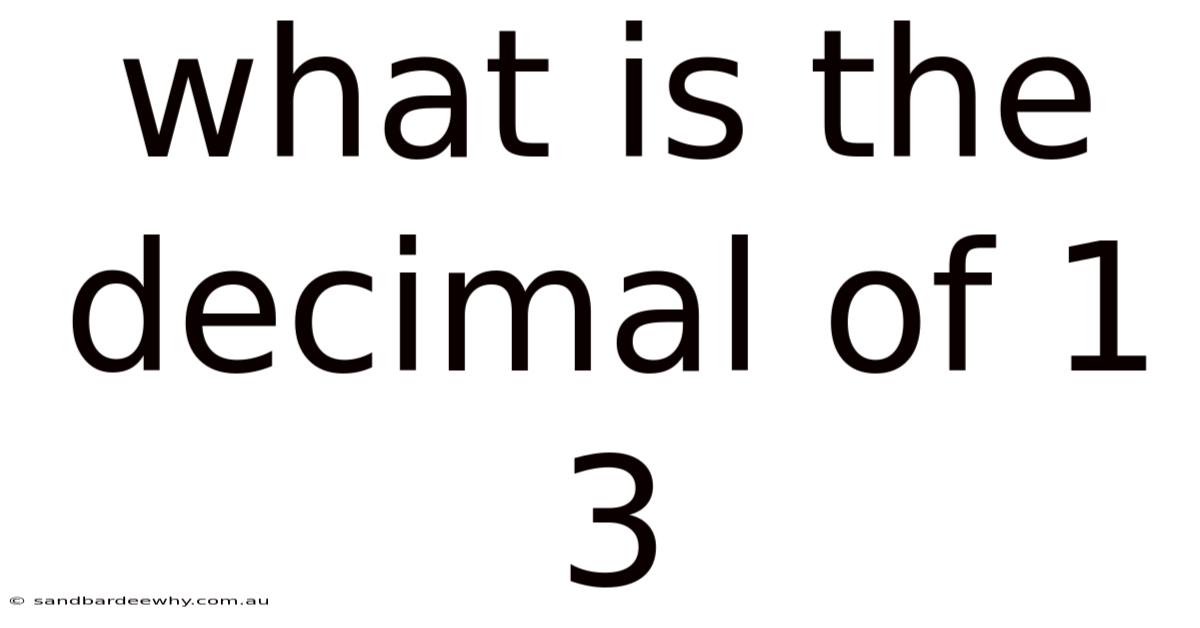
Table of Contents
Imagine you're baking a cake, and the recipe calls for "1 ⅓ cups of flour." You know you need one full cup, but what about that "⅓"? It's not quite a whole cup, but it's more than just a sprinkle. You need a way to represent that portion accurately to get your cake just right. That's where decimals come in handy. They provide a precise way to express fractions, like that "⅓," in a format that's easy to understand and use in calculations. Understanding decimals is crucial for everyday tasks, from cooking to managing finances, and it all starts with grasping how fractions translate into this numerical system.
Converting fractions to decimals can seem like a magic trick at first, but it's really a straightforward process rooted in the principles of division. When you encounter a mixed number like 1 ⅓, you're dealing with a whole number (1) and a fraction (⅓). To express this as a decimal, you need to figure out what decimal value is equivalent to the fraction. This involves dividing the numerator (the top number) of the fraction by the denominator (the bottom number). The result is a decimal that, when added to the whole number, gives you the decimal representation of the mixed number. So, how exactly do we perform this conversion, and what does it tell us about the nature of numbers themselves? Let's delve deeper into the world of decimals and discover how to transform 1 ⅓ into its decimal form.
Main Subheading
The journey from fractions to decimals is a fascinating one, offering a more granular way to represent numbers that lie between whole integers. The beauty of the decimal system lies in its ability to express values with a high degree of precision, making it indispensable in fields like science, engineering, and finance. Unlike fractions, which require a numerator and a denominator, decimals use a base-10 system, where each digit to the right of the decimal point represents a fraction with a denominator that is a power of 10. This makes it incredibly easy to perform arithmetic operations, compare values, and visualize quantities.
Understanding the basics of decimals is fundamental to grasping more complex mathematical concepts. Each position after the decimal point has a specific name and value: tenths, hundredths, thousandths, and so on. This positional notation allows us to represent very small or very large numbers with relative ease. But beyond the practical applications, the conversion between fractions and decimals reveals deeper insights into the nature of numbers. Some fractions convert into terminating decimals, which have a finite number of digits after the decimal point, while others convert into repeating decimals, where a sequence of digits repeats indefinitely. This distinction leads us to explore the concepts of rational and irrational numbers and the infinite nature of the number line.
Comprehensive Overview
At its core, a decimal is a way of representing numbers that are not whole numbers. It is based on the base-10 system, which means that each digit in a decimal number represents a power of 10. The digits to the left of the decimal point represent whole numbers, while the digits to the right represent fractions with denominators that are powers of 10. For example, in the decimal 3.14, the '3' represents three whole units, the '1' represents one-tenth (1/10), and the '4' represents four-hundredths (4/100). This positional notation is what makes decimals so versatile and easy to use.
The scientific foundation of decimals lies in the concept of place value. Each digit in a number has a value that depends on its position. In the decimal system, the place values to the left of the decimal point are powers of 10 (1, 10, 100, 1000, etc.), while the place values to the right of the decimal point are negative powers of 10 (0.1, 0.01, 0.001, etc.). This system allows us to represent any real number, no matter how large or small, with a finite or repeating decimal representation. The use of base-10 is thought to have originated from the fact that humans have ten fingers, making it a natural choice for counting and arithmetic.
The history of decimals is intertwined with the development of numerical systems and mathematical notation. While the concept of representing fractions with a base-10 system dates back to ancient civilizations, the modern decimal notation with a decimal point was not widely adopted until the late 16th century. Key figures in the popularization of decimals include Simon Stevin, a Flemish mathematician who advocated for their use in his book "De Thiende" (The Tenth) in 1585. Stevin argued that decimals were easier to use for calculations than fractions and advocated for their adoption in everyday life. His work played a crucial role in the widespread acceptance of decimals in Europe and beyond.
Understanding the essential concepts of decimals involves recognizing the different types of decimal representations. Terminating decimals are those that have a finite number of digits after the decimal point, such as 0.25 or 0.5. These decimals represent fractions that can be expressed with a denominator that is a power of 10. Repeating decimals, on the other hand, have a sequence of digits that repeats indefinitely, such as 0.333... or 0.142857142857... These decimals represent fractions that cannot be expressed with a denominator that is a power of 10. The distinction between terminating and repeating decimals is important for understanding the nature of rational numbers.
Converting fractions to decimals involves dividing the numerator of the fraction by its denominator. For example, to convert the fraction ⅓ to a decimal, you would divide 1 by 3. The result is 0.333..., which is a repeating decimal. To convert a mixed number like 1 ⅓ to a decimal, you first convert the fraction part (⅓) to a decimal and then add it to the whole number part (1). In this case, ⅓ is equal to 0.333..., so 1 ⅓ is equal to 1 + 0.333..., which is 1.333.... Understanding this conversion process is essential for working with fractions and decimals interchangeably and for performing accurate calculations in various contexts.
Trends and Latest Developments
Current trends in the use of decimals revolve around increasing precision and computational efficiency. In scientific computing, for example, decimals are often represented with a high number of digits to ensure accurate results in complex simulations and calculations. The use of arbitrary-precision arithmetic libraries allows computers to perform calculations with decimals to any desired level of accuracy, overcoming the limitations of fixed-precision floating-point numbers. This is particularly important in fields like cryptography, where even small rounding errors can have significant consequences.
Data from various fields, such as finance and engineering, show a growing reliance on decimals for representing measurements and values. In financial markets, prices are often quoted to several decimal places to reflect small changes in value. In engineering, measurements are made with increasing precision, requiring the use of decimals to represent values accurately. This trend is driven by the increasing availability of high-precision measuring instruments and the need for greater accuracy in design and manufacturing processes.
Popular opinion on decimals is generally positive, with most people recognizing their importance in everyday life and various professions. However, some people may struggle with understanding and using decimals, particularly when it comes to converting fractions to decimals or performing complex calculations. This highlights the importance of effective math education and the need for clear and accessible explanations of decimal concepts. Online resources and educational tools can play a crucial role in helping people improve their understanding of decimals and their applications.
Professional insights into the use of decimals emphasize the importance of understanding the limitations of decimal representations. While decimals can provide a high degree of precision, they are not always able to represent numbers exactly. For example, the fraction ⅓ cannot be represented as a terminating decimal, and any decimal approximation will have some degree of error. This is important to keep in mind when performing calculations and interpreting results, particularly in situations where accuracy is critical. Professionals in fields like finance and engineering are trained to be aware of these limitations and to use appropriate methods for dealing with them.
The latest developments in decimal technology include the development of new algorithms and software tools for performing calculations with decimals more efficiently. For example, researchers are working on developing new methods for multiplying and dividing decimals that are faster and more accurate than traditional methods. These developments are driven by the increasing demand for high-performance computing in various fields and the need for efficient ways to process large amounts of decimal data. Additionally, there is ongoing research into new ways of representing decimals in computer memory to improve storage efficiency and reduce memory usage.
Tips and Expert Advice
One practical tip for working with decimals is to always pay attention to the units of measurement. When dealing with real-world problems, it's important to understand what the decimal represents in terms of the units being used. For example, if you are measuring the length of an object in meters, then a decimal like 2.5 meters represents two and a half meters. Keeping track of the units will help you avoid mistakes and ensure that your calculations are meaningful.
Another helpful tip is to use estimation to check your work when performing calculations with decimals. Before you start calculating, take a moment to estimate what the answer should be. This will give you a sense of whether your final answer is reasonable. For example, if you are adding 3.25 and 4.75, you can estimate that the answer should be around 8 (since 3 + 5 = 8). If your final answer is significantly different from your estimate, then you know you have made a mistake somewhere.
Expert advice on using decimals often emphasizes the importance of understanding the underlying mathematical concepts. Rather than simply memorizing rules and procedures, try to understand why decimals work the way they do. This will help you apply your knowledge to new situations and solve problems more effectively. For example, understanding the concept of place value will help you understand how to add, subtract, multiply, and divide decimals correctly.
When converting fractions to decimals, remember that some fractions will result in repeating decimals. In these cases, you can either round the decimal to a certain number of decimal places or use the repeating decimal notation (e.g., 0.333... or 0.3 with a bar over the 3). The choice of which method to use will depend on the level of accuracy required for the problem. In general, it's better to use the repeating decimal notation if you need to perform further calculations, as this will avoid rounding errors.
Finally, take advantage of the many online resources and tools that are available for working with decimals. There are websites that can convert fractions to decimals, calculators that can perform calculations with decimals, and tutorials that can help you understand decimal concepts. These resources can be invaluable for improving your understanding of decimals and for solving problems more efficiently. Don't be afraid to use them to your advantage.
FAQ
Q: What is a decimal? A: A decimal is a way of representing numbers that are not whole numbers, using a base-10 system. Digits to the right of the decimal point represent fractions with denominators that are powers of 10.
Q: How do I convert a fraction to a decimal? A: Divide the numerator (top number) of the fraction by the denominator (bottom number). The result is the decimal equivalent of the fraction.
Q: What is a repeating decimal? A: A repeating decimal is a decimal in which a sequence of digits repeats indefinitely, such as 0.333... or 0.142857142857...
Q: How do I round a decimal? A: To round a decimal, look at the digit to the right of the place you are rounding to. If that digit is 5 or greater, round up. If it is less than 5, round down.
Q: Why are decimals important? A: Decimals are important because they allow us to represent numbers with a high degree of precision and are widely used in science, engineering, finance, and everyday life.
Conclusion
In summary, decimals provide a precise and versatile way to represent numbers, bridging the gap between whole numbers and fractions. Understanding how to convert fractions to decimals, recognizing the different types of decimal representations, and applying practical tips for working with decimals are essential skills in various fields. From everyday tasks to complex scientific calculations, decimals play a crucial role in our understanding and manipulation of numerical data.
Now that you have a comprehensive understanding of decimals, it's time to put your knowledge into practice. Try converting different fractions to decimals, performing calculations with decimals, and exploring the various online resources available to enhance your skills. Share this article with your friends and colleagues, and let's continue to build a community of confident and competent decimal users!
Latest Posts
Latest Posts
-
Psi Exm For Mac Os 12 7 6
Nov 26, 2025
-
How To Say 20 In Spanish
Nov 26, 2025
-
How Many Oz Are In A Half Gallon
Nov 26, 2025
-
How Tall Is 50 Inches In Feet
Nov 26, 2025
-
Which Transformation Would Not Map The Rectangle Onto Itself
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about What Is The Decimal Of 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.