What Is The Percent For 1/3
sandbardeewhy
Nov 22, 2025 · 13 min read
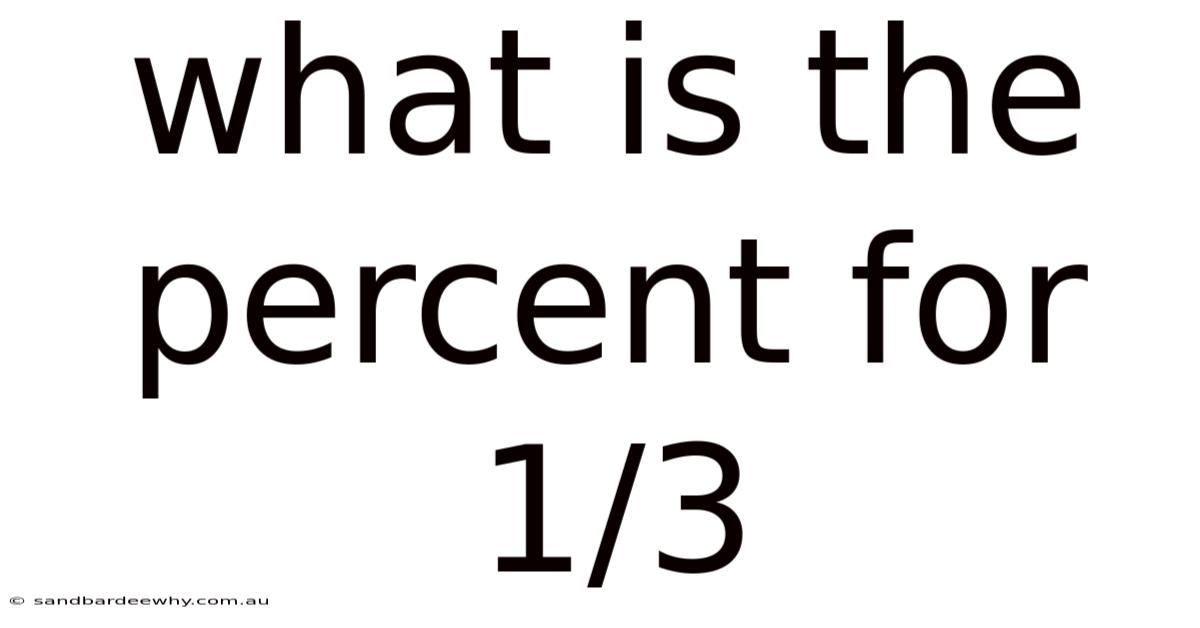
Table of Contents
Imagine you're sharing a pizza with two friends. You cut the pizza into three equal slices. Each of you gets one slice, which represents 1/3 of the whole pizza. But what if you wanted to express your share as a percentage? How would you convert that fraction into a familiar percentage? Understanding how to convert fractions to percentages, especially common fractions like 1/3, is a fundamental skill that finds applications in everyday scenarios, from calculating discounts to understanding statistical data.
The concept of converting fractions to percentages is not just a mathematical exercise; it's a practical tool that simplifies the way we interpret and compare proportions. In the realm of finance, understanding percentages helps in calculating returns on investments, interest rates, and profit margins. In science, percentages are used to express concentrations, errors, and statistical significance. Even in daily life, percentages appear in news reports, surveys, and product labels, making it essential to grasp their meaning and calculation. Let's explore how to determine the percentage equivalent of 1/3 and discuss the broader applications of this skill.
Understanding the Basics of Fractions and Percentages
Before diving into the specific conversion of 1/3 to a percentage, it's important to establish a solid understanding of what fractions and percentages represent. A fraction is a way to represent a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). For instance, in the fraction 1/3, the numerator is 1, and the denominator is 3. This means one part out of three equal parts.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, a percentage represents how many parts of something there are if the whole is divided into 100 parts. For example, 50% means 50 out of 100, or half of the whole.
The relationship between fractions and percentages is direct and convertible. Any fraction can be expressed as a percentage, and any percentage can be expressed as a fraction. This interconvertibility allows us to represent the same proportion in different formats, choosing the one that is most convenient or understandable for a particular context.
To convert a fraction to a percentage, you essentially need to find an equivalent fraction with a denominator of 100. If this isn't straightforward, you can use a simple mathematical operation: divide the numerator by the denominator, and then multiply the result by 100. This process effectively scales the fraction to a percentage.
Understanding this foundational concept is crucial for many practical applications. Whether you are calculating discounts while shopping, figuring out tips at a restaurant, or analyzing statistical data, the ability to fluently convert between fractions and percentages is an invaluable skill. It allows you to quickly grasp proportions and make informed decisions based on numerical information.
Converting 1/3 to a Percentage: Step-by-Step
The process of converting the fraction 1/3 to a percentage involves a simple calculation. Here's a step-by-step guide:
-
Divide the Numerator by the Denominator: The first step is to divide the numerator (1) by the denominator (3). This gives you a decimal value.
1 ÷ 3 = 0.3333...The result is a repeating decimal, approximately 0.3333.
-
Multiply by 100: To convert the decimal to a percentage, multiply the decimal by 100. This moves the decimal point two places to the right.
0.3333... × 100 = 33.33... -
Add the Percent Symbol: Finally, add the percent symbol (%) to the result to indicate that it is a percentage.
33.33...%
Therefore, 1/3 is approximately equal to 33.33%. The decimal representation of 1/3 is a repeating decimal, so the percentage is also a repeating decimal. In many practical contexts, it's common to round the percentage to a more manageable number, such as 33.3% or 33%.
This calculation demonstrates how fractions can be easily converted into percentages, providing a clear and concise way to express proportions. The ability to perform this conversion is essential for anyone dealing with numerical data, as it allows for easy comparison and interpretation of different proportions.
Practical Applications of Understanding Percentages
Understanding percentages, especially those derived from common fractions like 1/3, has numerous practical applications in various aspects of life. Here are a few examples:
-
Finance and Investments: In finance, percentages are used to calculate interest rates, returns on investments, and profit margins. For instance, if an investment yields a return of 1/3 of its initial value, it means the return is approximately 33.33%. This understanding helps investors make informed decisions by easily comparing different investment opportunities.
-
Retail and Discounts: Retailers often use percentages to express discounts on products. A discount of 33.33% on an item means the price is reduced by 1/3. This is a common promotional strategy that attracts customers by offering significant savings. Knowing how to calculate percentages helps consumers quickly determine the actual price they will pay after the discount.
-
Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions of populations or samples. For example, if a survey finds that 1/3 of respondents prefer a particular product, this is often reported as 33.33%. This makes the data easier to understand and compare with other statistics.
-
Education and Grading: In education, percentages are used to calculate grades and evaluate student performance. If a student scores 1/3 of the total points on a test, their grade might be expressed as 33.33%. This provides a clear indication of their performance relative to the maximum possible score.
-
Everyday Life: Percentages also appear in everyday situations, such as calculating tips at restaurants, understanding nutritional information on food labels, and interpreting news reports. For instance, a tip of 15% to 20% is commonly given at restaurants, and understanding percentages helps in calculating the correct amount to leave.
The ability to work with percentages is a fundamental skill that enhances financial literacy, improves decision-making, and facilitates understanding of numerical information in various contexts. Mastering percentage calculations allows individuals to navigate everyday situations with confidence and make well-informed choices.
Common Mistakes to Avoid When Calculating Percentages
When calculating percentages, it's easy to make mistakes that can lead to inaccurate results. Here are some common pitfalls to watch out for:
-
Forgetting to Multiply by 100: One of the most common mistakes is forgetting to multiply the decimal by 100 after dividing the numerator by the denominator. This step is crucial for converting the decimal into a percentage. Without it, the result remains a decimal fraction, not a percentage.
-
Incorrectly Identifying the Base Value: Percentages are always calculated in relation to a base value. Incorrectly identifying this base can lead to inaccurate calculations. For example, when calculating a percentage increase or decrease, it's important to use the original value as the base.
-
Rounding Errors: Rounding decimals too early in the calculation can introduce significant errors in the final percentage. It's best to perform the calculations with as many decimal places as possible and only round the final result to avoid accumulating rounding errors.
-
Confusing Percentage Points with Percentages: It's important to distinguish between percentage points and percentages. A percentage point is a simple arithmetic difference between two percentages. For instance, if a rate increases from 10% to 12%, that's an increase of 2 percentage points, or a 20% relative increase.
-
Misinterpreting Percentage Change: When calculating percentage change, it's essential to use the correct formula:
Percentage Change = [(New Value - Old Value) / Old Value] × 100Using the wrong formula or mixing up the new and old values can lead to incorrect percentage change calculations.
-
Assuming Percentages Are Always Additive: Percentages are not always additive. For example, if something increases by 50% and then decreases by 50%, it does not return to its original value. This is because the 50% decrease is calculated based on the new, higher value.
By being aware of these common mistakes and taking care to avoid them, you can improve the accuracy of your percentage calculations and make more informed decisions based on reliable data.
Trends and Latest Developments in Percentage Usage
The use of percentages continues to evolve with advancements in technology and changes in data presentation practices. Here are some current trends and developments:
-
Data Visualization: With the increasing availability of data, there's a growing trend towards using data visualization tools to present percentages in a more intuitive and accessible format. Charts, graphs, and infographics are used to communicate percentage data effectively, making it easier for audiences to understand complex information.
-
Interactive Dashboards: Interactive dashboards are becoming increasingly popular for presenting real-time data, including percentages. These dashboards allow users to explore data dynamically, filter information, and drill down into specific details, providing a more engaging and informative experience.
-
Artificial Intelligence (AI) and Machine Learning (ML): AI and ML technologies are being used to analyze large datasets and identify patterns and trends that can be expressed as percentages. These technologies can help organizations make data-driven decisions by uncovering insights that might not be apparent through traditional analysis methods.
-
Personalized Reporting: Personalized reporting is gaining traction, where data, including percentages, is tailored to individual users based on their preferences and needs. This ensures that users receive the most relevant information, presented in a way that is easy for them to understand.
-
Mobile Accessibility: With the proliferation of mobile devices, there's a growing emphasis on making percentage data accessible on smartphones and tablets. Mobile-friendly dashboards, reports, and visualizations are designed to provide users with access to critical information on the go.
-
Emphasis on Context: There's an increasing awareness of the importance of providing context when presenting percentages. Instead of simply showing a percentage, data presenters are now including explanations of what the percentage represents, how it was calculated, and what its implications are.
These trends reflect a broader movement towards making data more accessible, understandable, and actionable. By embracing these developments, individuals and organizations can leverage the power of percentages to make better-informed decisions and communicate insights effectively.
Tips and Expert Advice for Mastering Percentage Calculations
Mastering percentage calculations requires practice and a solid understanding of the underlying concepts. Here are some tips and expert advice to help you improve your skills:
-
Practice Regularly: The best way to become proficient in percentage calculations is to practice regularly. Work through various examples and exercises to reinforce your understanding and build your confidence.
-
Understand the Fundamentals: Make sure you have a solid grasp of the fundamental concepts of fractions, decimals, and percentages. Understanding how these concepts relate to each other is essential for performing accurate calculations.
-
Use Mental Math Techniques: Develop your mental math skills to perform simple percentage calculations quickly and easily. For example, knowing that 10% of a number is simply the number divided by 10 can help you estimate percentages in your head.
-
Break Down Complex Problems: When faced with a complex percentage problem, break it down into smaller, more manageable steps. This will make the problem less daunting and reduce the likelihood of errors.
-
Use Estimation Techniques: Before performing a calculation, estimate the answer to get a sense of what the result should be. This can help you identify potential errors and ensure that your calculations are reasonable.
-
Double-Check Your Work: Always double-check your work to ensure that you haven't made any mistakes. Review your calculations and compare your answer to your estimate to verify its accuracy.
-
Use Technology Wisely: While it's important to develop your manual calculation skills, don't hesitate to use technology to your advantage. Calculators, spreadsheets, and online tools can help you perform complex percentage calculations quickly and accurately.
-
Seek Feedback: Ask for feedback from teachers, mentors, or peers to identify areas where you can improve your skills. Constructive criticism can help you refine your techniques and avoid common mistakes.
By following these tips and advice, you can enhance your understanding of percentage calculations and become more confident in your ability to work with percentages in various contexts.
FAQ About Percentages
Q: What is the formula for converting a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100. The formula is:
Percentage = (Numerator / Denominator) × 100
Q: How do you calculate a percentage increase?
A: To calculate a percentage increase, use the following formula:
Percentage Increase = [(New Value - Old Value) / Old Value] × 100
Q: How do you calculate a percentage decrease?
A: To calculate a percentage decrease, use the following formula:
Percentage Decrease = [(Old Value - New Value) / Old Value] × 100
Q: What is the difference between a percentage and a percentage point?
A: A percentage is a way of expressing a number as a fraction of 100. A percentage point is a simple arithmetic difference between two percentages. For example, if a rate increases from 10% to 12%, that's an increase of 2 percentage points.
Q: How do you find the percentage of a number?
A: To find the percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, to find 25% of 80, multiply 80 by 0.25 (25/100).
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when calculating percentage increases. For example, if a value doubles, it has increased by 100%, and if it triples, it has increased by 200%.
Q: How do you convert a percentage back to a fraction?
A: To convert a percentage back to a fraction, divide the percentage by 100 to get a decimal, and then express the decimal as a fraction. Simplify the fraction if possible.
Conclusion
Understanding what is the percent for 1/3, which is approximately 33.33%, is more than just a mathematical exercise; it's a practical skill that enhances your ability to interpret and analyze proportions in various real-world scenarios. From calculating discounts and understanding financial data to interpreting statistics and making informed decisions, percentages play a crucial role in everyday life.
By mastering the fundamentals of percentage calculations, avoiding common mistakes, and staying up-to-date with the latest trends, you can improve your numerical literacy and make better-informed decisions. Whether you're a student, a professional, or simply someone who wants to enhance their understanding of the world around them, the ability to work with percentages is an invaluable asset.
Now that you have a comprehensive understanding of what is the percent for 1/3 and the broader applications of percentages, take the next step and apply this knowledge to your own life. Practice calculating percentages in different contexts, explore data visualization tools, and seek out opportunities to use your skills in real-world situations. Share your insights and experiences with others, and continue to expand your knowledge of this essential mathematical concept.
Latest Posts
Latest Posts
-
How To Find Expacted Valu In Chi Square
Nov 22, 2025
-
How Many Lbs Is 24 Oz
Nov 22, 2025
-
How To Find Discontinuities Of Rational Function
Nov 22, 2025
-
Current Phase Of The Moon As An Emoji
Nov 22, 2025
-
How To Find If A Function Is Even Or Odd
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent For 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.