What Percent Is 14 Of 20
sandbardeewhy
Nov 21, 2025 · 9 min read
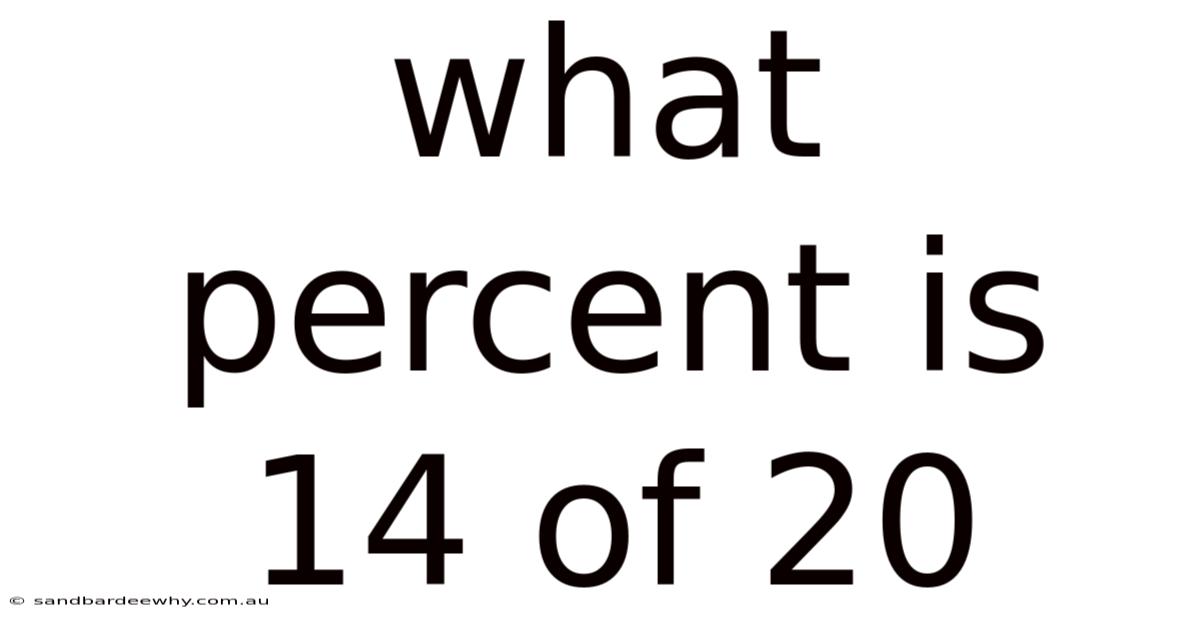
Table of Contents
The aroma of freshly brewed coffee filled the air as Sarah prepared for her online math class. A seemingly simple question flashed on her screen: "What percent is 14 of 20?" She frowned slightly, remembering similar problems from her school days. While the basic formula was familiar, she knew many students struggled with the underlying concept of percentages and their real-world applications.
Across town, David was reviewing his company's sales figures. He needed to quickly determine what percentage of their monthly target each department had achieved. The numbers swam before his eyes, and he wished there was a more intuitive way to grasp these proportions. He sighed, realizing that a solid understanding of percentage calculations was crucial for making informed business decisions.
Main Subheading
Percentages are an integral part of everyday life, from calculating discounts at the mall to understanding statistics in the news. The question "What percent is 14 of 20?" is a fundamental percentage problem that highlights the relationship between a part and a whole. Mastering this concept is essential for developing a strong foundation in mathematics and for navigating various practical situations.
In essence, a percentage represents a proportion out of one hundred. It provides a standardized way to compare different ratios, making it easier to understand the relative size of one quantity compared to another. Calculating percentages involves understanding the relationship between the base (the whole), the part (the portion of the whole), and the percentage itself. The ability to solve percentage problems empowers us to make informed decisions and interpret data accurately.
Comprehensive Overview
At its core, a percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." This concept allows us to easily compare different proportions, regardless of the size of the original whole. For example, saying that 14 out of 20 apples are red doesn't immediately convey the same sense of proportion as saying that 70% of the apples are red. The percentage provides a standardized metric for comparison.
The mathematical foundation of percentages lies in the concept of ratios and proportions. A ratio compares two quantities, while a proportion states that two ratios are equal. In the case of "What percent is 14 of 20?", we are essentially setting up a proportion: 14/20 = x/100, where 'x' represents the percentage we are trying to find. Solving for 'x' involves cross-multiplication and division, ultimately leading us to the percentage value.
Historically, the use of percentages can be traced back to ancient Rome, where calculations involving hundredths were used for taxation and commerce. However, the modern symbol for percent (%) only appeared much later, evolving from various abbreviations for per cento during the 15th century. The widespread adoption of the decimal system further solidified the importance of percentages as a standard tool for expressing proportions.
The fundamental formula for calculating percentages is:
Percentage = (Part / Whole) * 100
In our example, the "part" is 14 and the "whole" is 20. Therefore, to find what percent 14 is of 20, we apply the formula:
Percentage = (14 / 20) * 100
Percentage = 0.7 * 100
Percentage = 70%
Therefore, 14 is 70% of 20. This simple calculation demonstrates the core principle of percentage calculations, highlighting the relationship between the part, the whole, and the resulting percentage value. Understanding this relationship is crucial for tackling more complex percentage problems.
Beyond the basic formula, several related concepts are essential for a comprehensive understanding of percentages. Percentage increase and decrease, for instance, involve calculating the relative change between two values. Percentage error is used to quantify the accuracy of a measurement or estimate. These concepts build upon the fundamental principles of percentage calculations, providing a more nuanced understanding of how to use percentages in different contexts.
Trends and Latest Developments
In today's data-driven world, percentages are more relevant than ever. From financial analysis to scientific research, percentages are used extensively to summarize data, identify trends, and make informed decisions. A recent trend is the increasing use of interactive data visualizations that incorporate percentages to communicate complex information in a more accessible format. These visualizations often allow users to explore the data and see how different factors contribute to the overall percentage.
Furthermore, the rise of e-commerce has made understanding discounts and promotions even more critical for consumers. Retailers frequently use percentages to advertise sales and special offers, making it essential for shoppers to quickly calculate the actual price reduction. This has led to the development of various online tools and calculators that simplify percentage calculations, empowering consumers to make informed purchasing decisions.
According to a recent study by the National Center for Education Statistics, a significant percentage of adults struggle with basic numeracy skills, including percentage calculations. This highlights the need for continued emphasis on mathematics education, particularly in areas that have direct relevance to everyday life. Addressing this gap in numeracy skills can empower individuals to make better financial decisions, understand health statistics, and participate more effectively in civic life.
Professional insights suggest that a strong understanding of percentages is not only valuable for personal finance and everyday decision-making but also crucial for career advancement in many fields. Employers across various industries are increasingly seeking candidates with strong analytical and quantitative skills, including the ability to interpret and analyze data presented as percentages. Developing proficiency in percentage calculations can therefore open up a wide range of career opportunities.
Moreover, the use of percentages in statistical analysis is constantly evolving. Researchers are developing new methods for analyzing data that incorporate percentages in more sophisticated ways. For example, Bayesian statistics often relies on expressing probabilities as percentages to quantify the uncertainty associated with different hypotheses. These advanced techniques are pushing the boundaries of statistical analysis and providing new insights into complex phenomena.
Tips and Expert Advice
Calculating percentages can be simplified by using a few practical tips and tricks. First, remember the basic formula: Percentage = (Part / Whole) * 100. Always identify the "part" and the "whole" correctly. The "whole" is the total amount or the reference value, while the "part" is the portion of the whole that you are interested in. For example, in the question "What percent is 14 of 20?", 20 is the whole and 14 is the part.
Next, convert the fraction (Part / Whole) into a decimal by performing the division. This step makes it easier to multiply by 100. In our example, 14/20 = 0.7. Multiplying this decimal by 100 gives you the percentage: 0.7 * 100 = 70%. This simple process can be applied to any percentage problem, regardless of the specific numbers involved.
Another helpful tip is to use benchmark percentages to estimate values. For example, 50% represents half of the whole, 25% represents a quarter, and 10% represents one-tenth. By knowing these benchmarks, you can quickly estimate the percentage value without performing a precise calculation. For instance, if you need to find what percent 26 is of 50, you can quickly estimate that it is slightly more than 50% since 26 is slightly more than half of 50.
Furthermore, practice solving different types of percentage problems to build your confidence and familiarity. Start with simple problems and gradually move on to more complex scenarios. You can find numerous online resources and practice worksheets that offer a variety of percentage problems. Regularly practicing these problems will help you develop a deeper understanding of the concepts and improve your problem-solving skills.
In real-world applications, be mindful of the context and the units of measurement. When dealing with percentage changes, pay attention to whether the change is an increase or a decrease. When comparing percentages, ensure that they are calculated based on the same whole. Misinterpreting the context or the units can lead to incorrect conclusions. For example, a 10% increase followed by a 10% decrease does not result in the original value.
Finally, utilize technology to simplify percentage calculations when appropriate. Calculators, spreadsheets, and online tools can quickly and accurately perform complex percentage calculations. However, it is important to understand the underlying concepts and not rely solely on technology. Technology should be used as a tool to enhance your understanding and efficiency, not as a substitute for critical thinking and problem-solving skills.
FAQ
Q: What is a percentage? A: A percentage is a way of expressing a number as a fraction of 100. It represents a proportion out of one hundred, allowing for easy comparison of different ratios.
Q: How do I calculate what percent one number is of another? A: Use the formula: Percentage = (Part / Whole) * 100. Identify the "part" (the portion of the whole) and the "whole" (the total amount or reference value).
Q: What is the difference between percentage increase and percentage decrease? A: Percentage increase refers to the relative increase between two values, while percentage decrease refers to the relative decrease between two values. The formulas for calculating these are:
- Percentage Increase = [(New Value - Original Value) / Original Value] * 100
- Percentage Decrease = [(Original Value - New Value) / Original Value] * 100
Q: How can I use percentages in everyday life? A: Percentages are used for calculating discounts, understanding statistics, interpreting financial data, and making informed decisions in various contexts.
Q: Is it possible for a value to increase by more than 100%? A: Yes, a value can increase by more than 100%. For example, if a value doubles, it has increased by 100%. If it triples, it has increased by 200%, and so on.
Conclusion
Understanding percentages is crucial for success in academics, personal finance, and professional life. By mastering the basic formula and practicing regularly, you can confidently tackle percentage problems in any situation. Remember that percentages provide a standardized way to compare proportions, allowing you to make informed decisions and interpret data accurately.
Now that you have a solid grasp of percentage calculations, take the next step and apply your knowledge to real-world scenarios. Whether it's calculating discounts while shopping, analyzing sales data at work, or understanding statistics in the news, your newfound skills will empower you to navigate the world with greater confidence and clarity. Share this article with your friends and colleagues to help them master percentages too!
Latest Posts
Latest Posts
-
2 Gallons Is How Many Pounds
Nov 21, 2025
-
Which Of The Following Statements About Carbohydrates Is Not True
Nov 21, 2025
-
How Did Cornelius Vanderbilt Acquired His Wealth
Nov 21, 2025
-
How Many Units Are In Ap Psychology
Nov 21, 2025
-
What Is The Percentage Of 34
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 14 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.