What Percent Is 3 Of 44
sandbardeewhy
Nov 27, 2025 · 9 min read
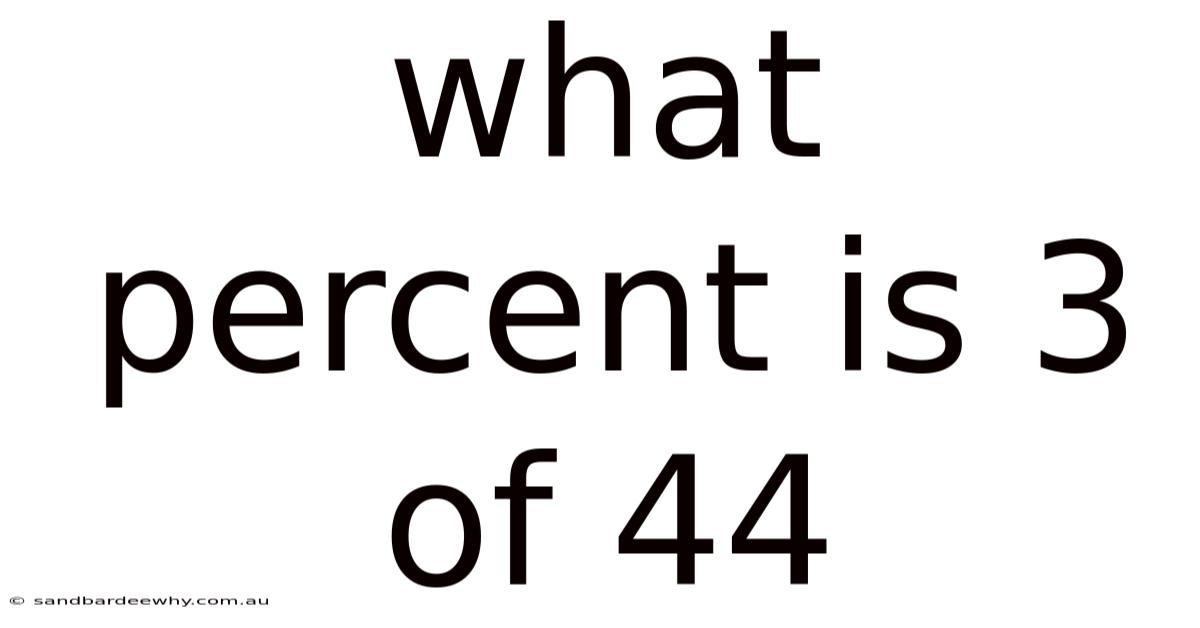
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a crate overflowing with vibrant red apples. The farmer tells you he has 44 apples in total, and you decide to buy just 3 of them. Later, you start wondering: what percentage of the entire crate did you actually purchase? This simple scenario highlights the everyday relevance of understanding percentages.
We encounter percentages constantly, from calculating discounts at our favorite stores to interpreting statistics in news reports. Knowing how to accurately determine what percent one number is of another is a fundamental skill, applicable in countless personal and professional situations. So, let's delve into understanding exactly what percent 3 is of 44, and equip ourselves with the knowledge to tackle similar calculations with confidence.
Understanding Percentages: The Basics
Percentages are a fundamental concept in mathematics and are used extensively in everyday life. Understanding what they represent and how to calculate them is crucial for making informed decisions and interpreting data accurately.
A percentage is essentially a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." So, when we say "50 percent," we mean 50 out of every 100, or 50/100. This can be further simplified to the fraction 1/2 or the decimal 0.5. Therefore, percentages provide a standardized way to compare proportions, making it easier to understand relative sizes and changes. They are used to represent everything from discounts and interest rates to statistical data and survey results. The power of percentages lies in their ability to provide a common framework for understanding and comparing different quantities.
The concept of percentages dates back to ancient Rome. As the Roman Empire expanded, taxes were often calculated as a fraction of the value of goods being sold. These fractions were often expressed in hundredths, a precursor to the modern percentage. However, the widespread use of percentages as we know them today didn't become common until the 15th century. With the rise of arithmetic and the development of standardized notations, percentages became an increasingly useful tool for commerce, finance, and scientific analysis. Today, percentages are an integral part of mathematics and are taught in schools worldwide as a basic and essential skill.
A Comprehensive Look at Percentage Calculations
To truly grasp what percent 3 is of 44, we need to dive into the core principles of percentage calculations. This involves understanding the relationship between parts, wholes, and the percentage itself. The fundamental formula that governs these calculations is:
(Part / Whole) * 100 = Percentage
Here, the "part" represents the specific quantity we're interested in, the "whole" represents the total quantity or the reference value, and the "percentage" expresses the part as a fraction of the whole, scaled to 100.
Let's break this down further with some examples:
- Finding a percentage of a whole: If you want to find 20% of 50, you would first convert the percentage to a decimal (20% = 0.20) and then multiply it by the whole (0.20 * 50 = 10). So, 20% of 50 is 10.
- Finding what percentage one number is of another: This is precisely what we're doing when we ask, "What percent is 3 of 44?" We'll solve this shortly.
- Finding the whole when you know the percentage and the part: If you know that 15 is 30% of a number, you can find the number by dividing the part by the percentage expressed as a decimal (15 / 0.30 = 50). So, 15 is 30% of 50.
The ability to manipulate this formula is crucial for solving a variety of percentage-related problems. It allows us to move beyond rote memorization and develop a deeper understanding of the relationships between quantities and their proportions.
Applying the Formula to Our Problem: What Percent is 3 of 44?
Now, let's apply this knowledge to our initial question: what percent is 3 of 44? Here, 3 is the "part" and 44 is the "whole." Using the formula:
(3 / 44) * 100 = Percentage
First, we divide 3 by 44:
3 / 44 ≈ 0.06818
Then, we multiply the result by 100 to express it as a percentage:
- 06818 * 100 ≈ 6.818%
Therefore, 3 is approximately 6.818% of 44.
In practical terms, this means that if you have 44 items and take 3 of them, you've taken approximately 6.818% of the total.
Why Understanding Decimals is Key
Notice how we converted the fraction 3/44 into a decimal before multiplying by 100. This conversion is a crucial step in accurately calculating percentages. Decimals provide a standardized way to represent fractions, making it easier to perform arithmetic operations.
Understanding the relationship between fractions, decimals, and percentages is essential for mastering percentage calculations. Being able to fluently convert between these forms allows for flexibility and accuracy in problem-solving.
Current Trends and Applications of Percentage Calculations
Percentage calculations are not static; they evolve with societal and technological changes. Today, we see percentages used in increasingly sophisticated ways, driven by data analysis, machine learning, and the need for clearer communication.
One prominent trend is the use of percentages in data visualization. Charts and graphs often display data as percentages to highlight proportions and trends. This allows viewers to quickly grasp the significance of data points and make informed decisions. For example, a pie chart might show the market share of different companies in a particular industry, with each slice representing a percentage of the total market. Similarly, bar graphs might use percentages to compare the performance of different products or services over time. The goal is always to make complex information more accessible and understandable.
Another significant development is the application of percentages in financial modeling and investment analysis. Investors use percentages to calculate returns on investment, assess risk, and compare the performance of different assets. For example, they might calculate the percentage increase or decrease in the price of a stock over a certain period or the percentage yield of a bond. These calculations help investors make informed decisions about where to allocate their capital. The use of sophisticated software and algorithms has made these calculations more precise and efficient, allowing investors to manage their portfolios more effectively.
Finally, the rise of e-commerce has further increased the importance of percentage calculations. Online retailers use percentages to offer discounts, calculate sales tax, and determine shipping costs. Consumers need to understand percentages to compare prices, evaluate deals, and make sure they are getting the best value for their money. The transparency and accessibility of online pricing have made consumers more aware of percentages and their impact on purchasing decisions.
Expert Tips for Mastering Percentage Calculations
While the basic formula for calculating percentages is straightforward, applying it effectively in real-world scenarios requires practice and attention to detail. Here are some expert tips to help you master percentage calculations:
-
Always identify the "part" and the "whole" correctly: This is the most crucial step in any percentage calculation. Make sure you understand which quantity represents the portion you are interested in and which quantity represents the total or reference value. Confusing the part and the whole will lead to incorrect results. For example, if you are calculating the percentage increase in sales, the "part" is the amount of the increase, and the "whole" is the original sales figure.
-
Convert percentages to decimals or fractions carefully: When performing calculations, it's essential to convert percentages to decimals or fractions correctly. To convert a percentage to a decimal, divide it by 100. For example, 25% becomes 0.25. To convert a percentage to a fraction, write it as a fraction with a denominator of 100 and simplify if possible. For example, 75% becomes 75/100, which simplifies to 3/4. Using the wrong conversion can lead to significant errors in your calculations.
-
Use estimation to check your answers: Before performing a percentage calculation, try to estimate the answer mentally. This will help you identify any obvious errors in your calculations. For example, if you are calculating 10% of 50, you know the answer should be close to 5. If you get an answer of 500, you know you have made a mistake. Estimation is a valuable tool for building confidence and accuracy in your percentage calculations.
-
Practice regularly with real-world examples: The best way to master percentage calculations is to practice them regularly with real-world examples. Look for opportunities to use percentages in your daily life, such as calculating discounts at the store, figuring out tips at a restaurant, or analyzing financial data. The more you practice, the more comfortable and confident you will become with percentage calculations.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage increase?
A: To calculate a percentage increase, use the formula: [(New Value - Original Value) / Original Value] * 100.
Q: What's the difference between percentage and percentage points?
A: A percentage is a proportion out of 100. Percentage points refer to the arithmetic difference between two percentages. For example, if a rate increases from 10% to 12%, that's a 2 percentage point increase, or a 20% increase relative to the original 10%.
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator, then multiply by 100. For example, to convert 1/4 to a percentage, calculate (1 / 4) * 100 = 25%.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when dealing with increases or growth. For example, if a company's revenue doubles, that's a 100% increase, and if it triples, that's a 200% increase.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include confusing the part and the whole, incorrectly converting percentages to decimals or fractions, and not using estimation to check your answers. Always double-check your work to avoid these errors.
Conclusion
In summary, determining what percent 3 is of 44 involves a simple yet powerful formula: (Part / Whole) * 100. In this case, the answer is approximately 6.818%. Understanding how to calculate percentages is a vital skill, applicable in numerous real-world scenarios, from shopping and finance to data analysis and everyday decision-making.
Now that you've grasped the core principles and practical applications of percentage calculations, it's time to put your knowledge to the test. Try applying these techniques to other scenarios you encounter in your daily life. Calculate discounts, analyze financial data, or simply estimate proportions. The more you practice, the more confident and proficient you will become in using percentages to make informed decisions and solve problems. Share this article with your friends and family so they too can improve their understanding of this essential mathematical concept!
Latest Posts
Latest Posts
-
How To Find Force Of A Spring
Nov 27, 2025
-
What Is The Difference Between A Jesuit And A Catholic
Nov 27, 2025
-
How Many Ounces Is 1 2 L
Nov 27, 2025
-
How Do You Find Original Price Of Discounted Item
Nov 27, 2025
-
How Many Pores In The Human Body
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 Of 44 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.