What Percent Of 20 Is 7
sandbardeewhy
Nov 28, 2025 · 11 min read
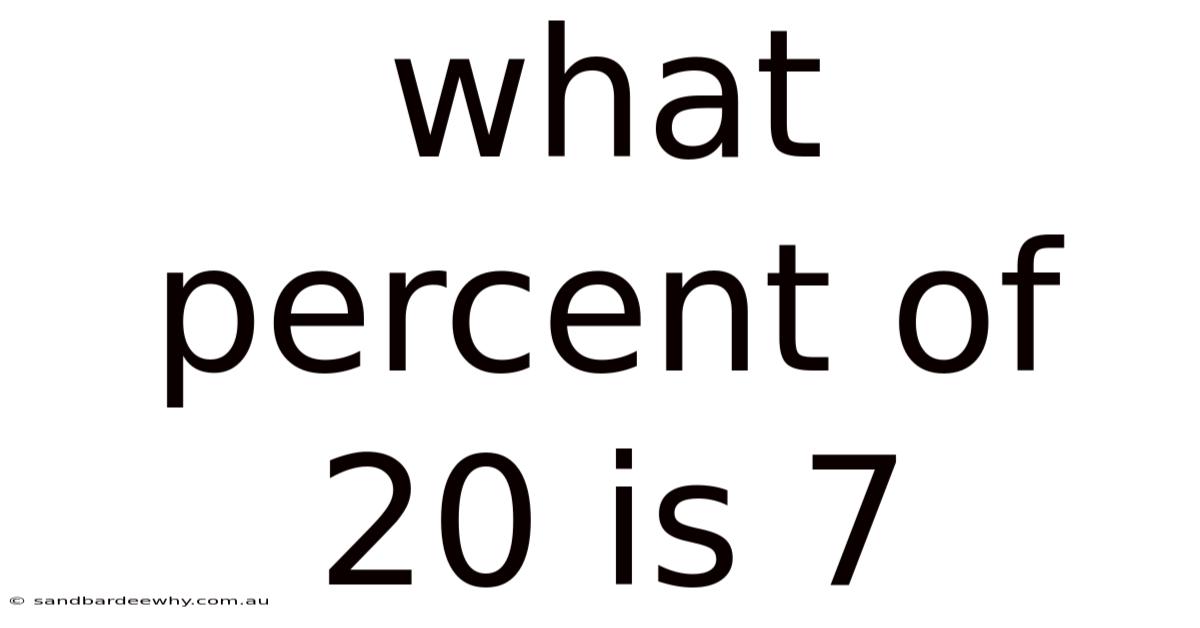
Table of Contents
Imagine you're at a farmers market, eyeing a basket of vibrant red apples. The sign says "20 apples for $10," but you only need 7. How much should you pay? This everyday scenario boils down to calculating a percentage: what percent of 20 is 7? This isn't just a mathematical exercise; it's a practical skill we use constantly, from splitting bills at a restaurant to understanding discounts at the store.
Understanding percentages is crucial in numerous aspects of life. From calculating discounts and taxes to understanding statistics and financial reports, percentages are a fundamental tool for informed decision-making. Many might find it intimidating at first glance, but mastering percentages opens doors to better comprehension of the world around us. In this article, we will explore a straightforward method for determining what percent of 20 is 7 and delve deeper into the practical applications of such calculations.
Figuring Out Percentage Basics
To properly understand how to calculate percentages, it's essential to lay the groundwork with some foundational concepts. Percentage calculations are not just abstract math, but practical tools used daily in various scenarios. Let's delve into the core principles of percentages.
At its core, a percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, when we say "50 percent," we mean 50 out of 100, often written as 50%. Percentages are used to express proportions, ratios, or changes relative to a whole. They provide a standardized way to compare different quantities, making it easier to understand and interpret data. Whether you're calculating a discount at a store, determining a tip at a restaurant, or analyzing financial data, percentages offer a clear and concise way to represent proportional relationships.
Percentages can be expressed in different forms, each useful in various contexts. The three primary forms are: percentage form, decimal form, and fraction form. The percentage form is the most common, written with the percent sign (%). For example, 25% represents 25 out of 100. The decimal form is obtained by dividing the percentage by 100. So, 25% becomes 0.25. This form is particularly useful in calculations because it can be directly used in multiplication and division. The fraction form represents the percentage as a fraction with a denominator of 100. Thus, 25% can be written as 25/100, which simplifies to 1/4. Understanding these forms is essential for converting between them and applying them in different scenarios.
To convert between these forms, it's crucial to know the basic rules. To convert a percentage to a decimal, divide the percentage by 100. For example, to convert 75% to a decimal, you would divide 75 by 100, resulting in 0.75. To convert a decimal to a percentage, multiply the decimal by 100. For instance, to convert 0.8 to a percentage, you would multiply 0.8 by 100, resulting in 80%. Converting a percentage to a fraction involves writing the percentage as a fraction with a denominator of 100 and then simplifying the fraction if possible. For example, 40% can be written as 40/100, which simplifies to 2/5. To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100. For example, to convert 3/4 to a percentage, you would divide 3 by 4, resulting in 0.75, and then multiply by 100, resulting in 75%.
These conversions are vital for accurate calculations. For example, when calculating a percentage increase or decrease, it's often easier to work with decimals. Similarly, when comparing proportions, fractions can provide a clearer visual representation. By mastering these conversions, you can seamlessly switch between different forms, making percentage calculations more intuitive and efficient. Understanding these fundamental concepts is crucial for tackling more complex percentage-related problems, providing a solid foundation for understanding and applying percentages in everyday situations.
Comprehensive Overview
Calculating "what percent of 20 is 7" involves a simple but fundamental mathematical process. To begin, we need to set up the problem as a mathematical equation. The basic formula to find what percentage one number is of another is:
(Part / Whole) * 100 = Percentage
In this case, 7 is the "part," and 20 is the "whole." The equation then becomes:
(7 / 20) * 100 = Percentage
This formula is universally applicable for finding percentages, whether you're calculating discounts, proportions, or any other scenario where you need to express a part of a whole as a percentage.
To solve the equation, divide 7 by 20. The result is 0.35. This decimal represents the proportion of 7 in relation to 20. However, to express this proportion as a percentage, we need to multiply it by 100. Multiplying 0.35 by 100 gives us 35. Therefore, 7 is 35% of 20.
This calculation illustrates that understanding the basic formula and performing the division and multiplication accurately are crucial steps in finding the percentage. The result, 35%, provides a clear and concise answer to the question, making it easy to understand the relationship between 7 and 20.
The concept of percentages has a rich history that dates back to ancient times. Though the modern concept of percentage developed in Europe during the Middle Ages, its roots can be traced to the practices of ancient civilizations. In ancient Rome, for example, calculations involving fractions of one hundred were common. Roman Emperor Augustus levied a tax of 1/100 on goods sold at auction, known as centesima rerum venalium. This illustrates an early application of percentage-like calculations in commerce and taxation. Over time, as trade and commerce expanded, the need for standardized methods of calculating proportions became increasingly important.
The formalization of percentages as we know them today occurred during the 15th century. As arithmetic notations became more standardized, the use of percentages gained popularity. The percent sign "%" evolved from various symbols used to denote "per cento," an Italian term meaning "out of one hundred." By the 17th century, percentages were widely used in Europe for financial calculations, statistical analysis, and various other applications. The adoption of percentages simplified calculations and facilitated comparisons, making it easier to understand and interpret quantitative data. Today, percentages are an integral part of mathematics and are used extensively in various fields, including finance, economics, science, and everyday life.
Trends and Latest Developments
Recent trends indicate an increasing reliance on data-driven decision-making across various sectors, which further amplifies the importance of understanding percentages. Whether it's in finance, marketing, or healthcare, professionals are using data to make informed choices. The ability to accurately calculate and interpret percentages is becoming more critical than ever. For instance, in finance, investors analyze percentage changes in stock prices to make investment decisions. In marketing, businesses track conversion rates and customer retention rates as percentages to evaluate the effectiveness of their strategies. In healthcare, understanding percentages helps in interpreting clinical trial results and assessing patient outcomes.
According to recent studies, proficiency in mathematical skills, including percentage calculations, is directly linked to better job performance and career advancement. Employers increasingly value candidates who can analyze data and draw meaningful conclusions from it. This trend highlights the importance of mathematics education and the need for individuals to develop strong quantitative skills. Educational institutions are also recognizing this need and are placing greater emphasis on teaching practical math skills that students can apply in real-world scenarios. This includes incorporating more hands-on activities and real-life examples in mathematics curricula to make learning more engaging and relevant.
In popular opinion, the understanding and application of percentages are often underestimated. Many people view percentage calculations as a basic math skill, but its importance in everyday life cannot be overstated. From calculating tips at restaurants to understanding interest rates on loans, percentages play a crucial role in personal finance and decision-making. There is a growing consensus that improving numeracy skills, including the ability to work with percentages, can empower individuals to make better financial choices and lead more informed lives. Financial literacy programs are increasingly focusing on teaching essential math skills, including percentage calculations, to help people manage their money more effectively.
Professional insights suggest that a solid understanding of percentages is also crucial for critical thinking and problem-solving. When presented with statistical data or quantitative information, individuals with strong percentage skills are better equipped to analyze the data and identify potential biases or inaccuracies. This ability is particularly important in today's information-rich environment, where we are constantly bombarded with data from various sources. Being able to critically evaluate information and make informed decisions based on data is a valuable skill in both personal and professional contexts. Therefore, mastering percentages is not just about performing calculations but also about developing the ability to think critically and make informed decisions.
Tips and Expert Advice
Calculating percentages accurately is a skill that can be honed with practice. One effective tip is to break down complex problems into smaller, more manageable steps. For example, when calculating a percentage increase or decrease, first, find the difference between the two values, and then divide that difference by the original value. Finally, multiply by 100 to express the result as a percentage. This step-by-step approach can help reduce errors and make the calculation process more straightforward. Another useful tip is to use estimation to check the reasonableness of your answer. Before performing the actual calculation, try to estimate the percentage mentally. This can help you identify potential mistakes and ensure that your final answer is within a reasonable range.
Real-world examples can significantly enhance your understanding of percentage calculations. Consider a scenario where you want to calculate the discount on an item at a store. If the original price is $50 and the discount is 20%, you can quickly calculate the discount amount by multiplying $50 by 0.20 (the decimal equivalent of 20%), resulting in $10. To find the sale price, subtract the discount amount from the original price: $50 - $10 = $40. Similarly, when calculating a tip at a restaurant, you can estimate 10% of the bill amount by moving the decimal point one place to the left. Then, double that amount to find 20%, or multiply it by 1.5 to find 15%. These practical examples illustrate how percentage calculations can be applied in everyday situations to make informed decisions.
Another expert tip is to familiarize yourself with common percentage benchmarks and their decimal equivalents. Knowing that 25% is equivalent to 1/4 or 0.25, 50% is equivalent to 1/2 or 0.5, and 75% is equivalent to 3/4 or 0.75 can significantly speed up your calculations. These benchmarks serve as reference points that allow you to quickly estimate percentages without having to perform detailed calculations. Additionally, practice using these benchmarks in real-life scenarios to reinforce your understanding and improve your ability to estimate percentages accurately. For example, if you need to calculate 25% of $80, you can quickly recall that 25% is equivalent to 1/4 and divide $80 by 4, resulting in $20. This approach not only saves time but also enhances your confidence in performing percentage calculations.
Another piece of expert advice is to leverage technology to your advantage. Numerous online calculators and mobile apps are available that can help you perform percentage calculations quickly and accurately. These tools can be particularly useful when dealing with complex calculations or when you need to verify your results. However, it's important not to rely solely on technology and to develop a strong understanding of the underlying mathematical concepts. Use calculators as a tool to assist you in your calculations but always strive to understand the principles behind them. By combining your knowledge of percentage calculations with the efficiency of technology, you can become proficient at solving percentage-related problems in any situation.
FAQ
Q: What is the formula for finding what percentage one number is of another?
A: The formula is (Part / Whole) * 100 = Percentage.
Q: How do I convert a percentage to a decimal?
A: Divide the percentage by 100. For example, 45% becomes 0.45.
Q: How do I convert a decimal to a percentage?
A: Multiply the decimal by 100. For example, 0.65 becomes 65%.
Q: Why are percentages important in everyday life?
A: Percentages are used in various everyday situations, such as calculating discounts, taxes, tips, interest rates, and understanding statistical data.
Q: Can I use a calculator to find percentages?
A: Yes, calculators can be helpful, but understanding the underlying mathematical concepts is crucial.
Conclusion
In summary, determining what percent of 20 is 7 involves applying a basic yet essential mathematical formula: (Part / Whole) * 100 = Percentage. In this case, (7 / 20) * 100 equals 35%, illustrating that 7 is 35% of 20. Mastering such percentage calculations is not merely an academic exercise but a practical skill with far-reaching implications in everyday life, from managing personal finances to making informed decisions in professional settings.
As you continue to navigate the quantitative aspects of life, honing your ability to calculate and interpret percentages will undoubtedly prove invaluable. Whether you're a student, a professional, or simply someone looking to enhance their financial literacy, remember that practice and understanding are key. Take the time to apply these skills in real-world scenarios, and don't hesitate to explore additional resources and tools that can further enhance your proficiency. We encourage you to try calculating various percentages in your daily routines. Share your experiences or any challenges you encounter in the comments below. Your engagement can help others learn and grow, making mathematics a more approachable and understandable subject for everyone.
Latest Posts
Latest Posts
-
Defamiliarization Ambiguity Semiotics Interpretation Close Reading
Nov 28, 2025
-
When Did The Market Revolution Start
Nov 28, 2025
-
Horned Lizards Use Their Horns To Defend
Nov 28, 2025
-
Half Man Half Horse Is Called What
Nov 28, 2025
-
How Many Inches In A Half Yard
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 20 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.