What Percent Of 300 Is 50
sandbardeewhy
Nov 27, 2025 · 10 min read
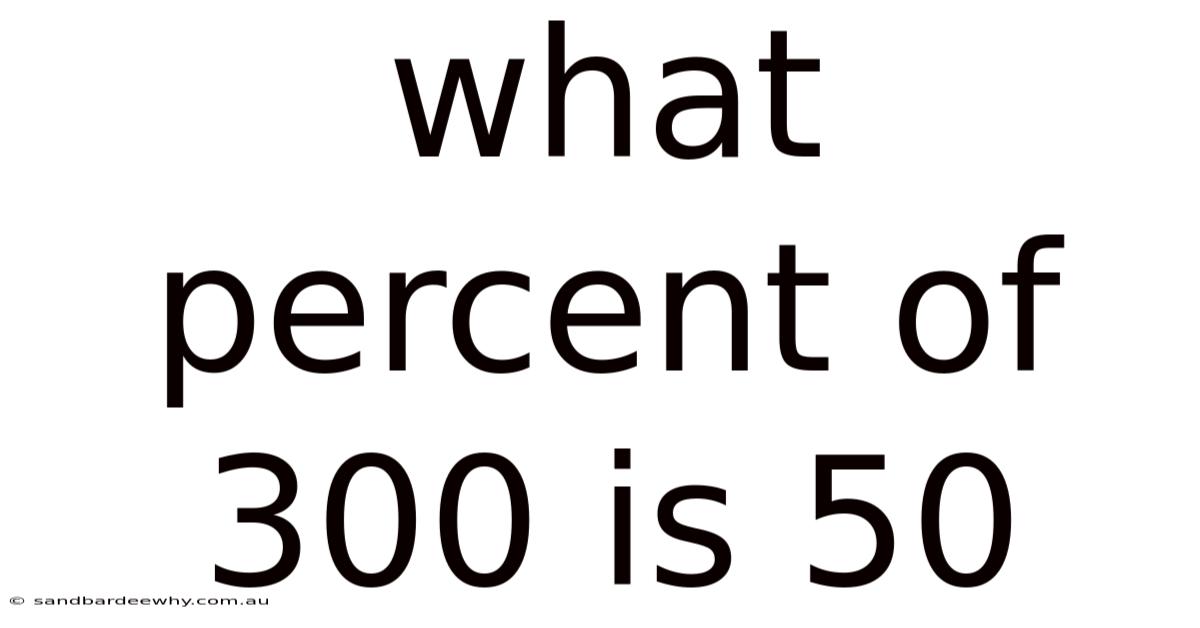
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a beautiful display of fresh, ripe apples. The sign reads, "300 Apples - Special Offer!" You only want 50 apples for your pie, and you're curious what fraction of the total that represents. This simple scenario introduces us to the world of percentages, a fundamental tool in everyday life, from calculating discounts to understanding statistical data.
Percentages are ubiquitous, appearing in financial reports, scientific studies, and even your favorite social media platforms. But what exactly is a percentage, and how do we calculate it? At its core, a percentage is simply a way to express a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." So, when we ask, "What percent of 300 is 50?", we're essentially asking, "How many parts out of one hundred is 50, when the whole is 300?"
Main Subheading
Understanding the concept of percentages is crucial for various applications. Whether you are a student grappling with math problems, a professional analyzing business data, or simply someone managing personal finances, percentages provide a clear and concise way to represent proportions and ratios. They allow us to compare different quantities relative to a common base of 100, making it easier to interpret and communicate information effectively.
Furthermore, grasping the underlying principles of percentage calculations empowers you to make informed decisions in various real-world scenarios. From evaluating investment opportunities based on returns to understanding the significance of survey results, percentages enable you to critically analyze data and draw meaningful conclusions. This knowledge enhances your ability to navigate complex situations and solve problems efficiently.
Comprehensive Overview
The concept of percentages dates back to ancient Rome, where calculations were often made in terms of hundredths. However, the widespread use of percentages in their modern form began in the 15th century. As trade and commerce flourished, the need for a standardized way to calculate interest, profits, and taxes became increasingly important. This led to the development and adoption of the percentage as a common unit of measure.
Mathematically, a percentage can be defined as a ratio or fraction expressed as a value out of 100. The symbol "%" is used to denote percentages. To convert a fraction or decimal to a percentage, you simply multiply it by 100. Conversely, to convert a percentage to a fraction or decimal, you divide it by 100. This simple conversion process allows us to seamlessly move between different representations of the same proportion.
The fundamental formula for calculating percentages is as follows:
Percentage = (Part / Whole) * 100
Where:
- Part is the value you want to express as a percentage of the whole.
- Whole is the total or reference value.
In the question "What percent of 300 is 50?", 50 is the "Part" and 300 is the "Whole." Therefore, the calculation would be:
Percentage = (50 / 300) * 100
Percentages are not just abstract mathematical concepts; they are powerful tools for comparison and analysis. For instance, if two students score differently on exams with different total marks, percentages can be used to compare their performances fairly. A student scoring 75 out of 100 has a percentage score of 75%, while a student scoring 150 out of 200 also has a percentage score of 75%. This shows that even though the raw scores are different, their relative performance is the same.
Another important aspect of percentages is their use in calculating percentage increase and decrease. These calculations are commonly used to track changes in sales figures, population growth, and stock prices. The formula for percentage increase is:
Percentage Increase = ((New Value - Original Value) / Original Value) * 100
Similarly, the formula for percentage decrease is:
Percentage Decrease = ((Original Value - New Value) / Original Value) * 100
These formulas provide valuable insights into the magnitude and direction of change over time.
The application of percentages extends beyond simple arithmetic. In statistics, percentages are used to represent the distribution of data and to calculate probabilities. For example, a survey might report that 60% of respondents prefer a certain product over its competitors. This percentage provides a clear and concise summary of the survey results. Similarly, in finance, percentages are used to calculate interest rates, returns on investment, and risk assessments.
Trends and Latest Developments
In today's data-driven world, the use of percentages is more prevalent than ever. Businesses rely heavily on percentage analysis to track key performance indicators (KPIs) and make strategic decisions. From monitoring sales growth and customer satisfaction to optimizing marketing campaigns and managing inventory, percentages play a vital role in every aspect of business operations.
One notable trend is the increasing use of interactive dashboards and data visualization tools to present percentage data in a more engaging and accessible format. These tools allow users to quickly identify trends, patterns, and outliers in the data, enabling them to make more informed decisions. For instance, a sales manager might use a dashboard to track the percentage of sales closed by each team member, allowing them to identify top performers and areas for improvement.
Another significant development is the growing importance of data literacy. As the volume of data continues to increase, it is crucial for individuals to be able to understand and interpret percentage data accurately. This includes being able to identify potential biases, understand the limitations of the data, and draw meaningful conclusions. Data literacy is becoming an essential skill in today's workforce, empowering individuals to make informed decisions in their professional and personal lives.
Furthermore, the rise of artificial intelligence (AI) and machine learning (ML) is also impacting the way percentages are used and interpreted. AI and ML algorithms can automatically analyze large datasets and identify patterns that might not be apparent to human analysts. These algorithms can also be used to predict future trends based on historical percentage data. For example, a retailer might use an AI algorithm to predict the percentage of customers who will purchase a certain product based on past sales data and other factors.
However, it is important to note that AI and ML algorithms are only as good as the data they are trained on. If the data is biased or incomplete, the algorithms may produce inaccurate or misleading results. Therefore, it is crucial to carefully evaluate the data used to train these algorithms and to validate the results they produce.
Tips and Expert Advice
Calculating percentages accurately and efficiently requires a combination of understanding the underlying principles and applying practical techniques. Here are some tips and expert advice to help you master percentage calculations:
-
Understand the Context: Before you start calculating percentages, make sure you understand the context of the problem. Identify the "Part" and the "Whole" accurately. Misidentifying these values will lead to incorrect results. For example, if you are calculating the percentage of students who passed an exam, the "Part" is the number of students who passed, and the "Whole" is the total number of students who took the exam.
-
Use a Calculator or Spreadsheet: While it is possible to calculate percentages manually, using a calculator or spreadsheet can save you time and reduce the risk of errors. Spreadsheets like Microsoft Excel and Google Sheets have built-in functions for calculating percentages, making the process even easier. Simply enter the "Part" and the "Whole" into the appropriate cells and use the formula "=Part/Whole*100" to calculate the percentage.
-
Practice Regularly: Like any mathematical skill, mastering percentage calculations requires practice. Work through a variety of problems to reinforce your understanding and build your confidence. Start with simple problems and gradually move on to more complex ones. You can find practice problems in textbooks, online resources, and even everyday situations.
-
Double-Check Your Results: Always double-check your results to ensure that they are reasonable and accurate. If you are calculating a percentage increase or decrease, make sure that the result is consistent with the direction of the change. For example, if the value has increased, the percentage change should be positive, and if the value has decreased, the percentage change should be negative.
-
Estimate Before Calculating: Before you perform the actual calculation, try to estimate the percentage. This will help you identify potential errors and ensure that your final answer is reasonable. For example, if you are calculating what percent of 300 is 50, you can estimate that the answer will be less than 20% because 50 is less than one-fifth of 300.
-
Be Aware of Common Mistakes: There are several common mistakes that people make when calculating percentages. One common mistake is to confuse the "Part" and the "Whole." Another common mistake is to forget to multiply by 100 when converting a fraction or decimal to a percentage. Be aware of these common mistakes and take steps to avoid them.
-
Use Percentages to Compare Data: Percentages are a powerful tool for comparing data. When comparing different quantities, express them as percentages of a common base. This will allow you to easily compare their relative values. For example, if you are comparing the sales performance of two different products, express their sales as percentages of total sales.
-
Understand Percentage Points: Be careful to distinguish between percentages and percentage points. A percentage point is the arithmetic difference between two percentages. For example, if the interest rate on a loan increases from 5% to 7%, the increase is 2 percentage points. However, the percentage increase is ((7-5)/5)*100 = 40%.
By following these tips and expert advice, you can improve your accuracy and efficiency in calculating percentages.
FAQ
Q: How do I calculate the percentage of a number?
A: To calculate the percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, to calculate 20% of 50, multiply 50 by 0.20 (20/100), which equals 10.
Q: How do I convert a percentage to a decimal?
A: To convert a percentage to a decimal, divide the percentage by 100. For example, 75% is equal to 0.75 (75/100).
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.45 is equal to 45% (0.45 * 100).
Q: What is the difference between a percentage increase and a percentage decrease?
A: A percentage increase represents the relative increase in a value, while a percentage decrease represents the relative decrease in a value. The formulas for calculating these are:
- Percentage Increase = ((New Value - Original Value) / Original Value) * 100
- Percentage Decrease = ((Original Value - New Value) / Original Value) * 100
Q: How are percentages used in everyday life?
A: Percentages are used in many aspects of everyday life, including calculating discounts, understanding financial reports, interpreting statistical data, and making informed decisions about purchases and investments.
Q: What does "percent" actually mean?
A: The word "percent" comes from the Latin per centum, meaning "out of one hundred".
Conclusion
In summary, understanding and calculating percentages is a fundamental skill with broad applications in various aspects of life. From managing personal finances to analyzing business data, percentages provide a clear and concise way to represent proportions and ratios. By mastering the basic principles and applying practical techniques, you can confidently navigate complex situations and make informed decisions. To answer our initial question: what percent of 300 is 50? The answer is 16.67%. This calculation, like many others involving percentages, underscores the importance of this mathematical tool.
Now, take the next step in enhancing your understanding of percentages. Explore more advanced topics, such as compound interest, statistical analysis, and data visualization. Practice calculating percentages in real-world scenarios and share your knowledge with others. By continuously learning and applying your skills, you can unlock the full potential of percentages and make informed decisions in all areas of your life. Share this article with your friends and colleagues to spread the knowledge and empower others to master the art of percentage calculations.
Latest Posts
Latest Posts
-
Opening Line Tale Of Two Cities
Nov 27, 2025
-
How Many Yards Are In 21 Feet
Nov 27, 2025
-
Why Is The Size Of Cells Limited
Nov 27, 2025
-
Puns In Romeo And Juliet Act 1
Nov 27, 2025
-
How Many Inches Are In 2 1 2 Yards
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 300 Is 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.