What Percent Of 60 Is 45
sandbardeewhy
Nov 23, 2025 · 13 min read
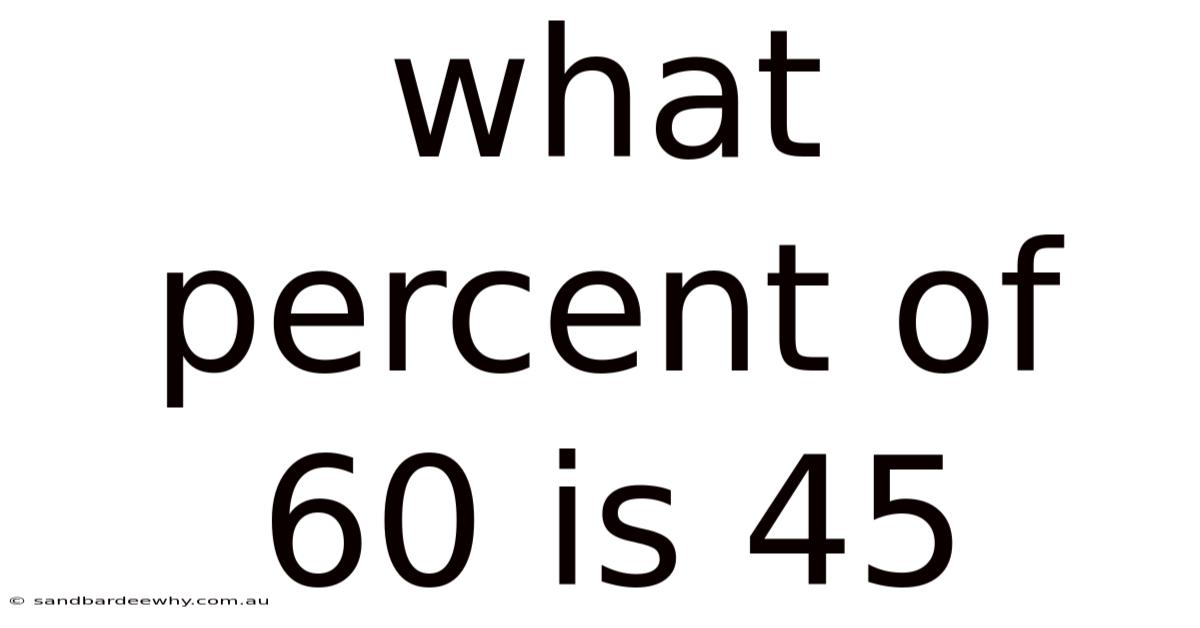
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a vibrant display of ripe mangoes. The sign says, "60 Mangoes for $X," but you only want 45. How do you figure out what percentage of the full price you'll actually pay? This everyday scenario highlights the importance of understanding percentages and how they relate to proportions. Figuring out "what percent of 60 is 45" isn't just a mathematical exercise; it's a practical skill applicable to shopping, budgeting, data analysis, and countless other situations.
This simple question unlocks a powerful tool for understanding proportions and making informed decisions. Whether you're calculating discounts, analyzing survey results, or even determining the composition of a chemical compound, knowing how to find what percentage one number represents of another is essential. Let's delve into the world of percentages and unravel the mystery of "what percent of 60 is 45," equipping you with the knowledge and skills to confidently tackle similar problems in any context.
Decoding Percentages: Finding the Proportion
At its core, determining what percent of 60 is 45 involves understanding the relationship between two numbers: the part (45) and the whole (60). A percentage is simply a way of expressing a number as a fraction of 100. In other words, it's a ratio that's been scaled to a base of 100, making it easy to compare different proportions. The word "percent" literally means "out of one hundred," derived from the Latin per centum. This inherent scaling property makes percentages a universally understood way to represent proportions, regardless of the specific units involved.
To find what percentage of 60 is 45, we're essentially asking: "What fraction of 60 does 45 represent, and how would we express that fraction as a number out of 100?" The fundamental concept is that the percentage we're looking for is the ratio of 45 to 60, multiplied by 100. This converts the ratio, which could be a decimal or a fraction, into a percentage. Understanding this basic principle is crucial, as it lays the foundation for solving a wide range of percentage-related problems. We use percentages daily to calculate sale prices, understand statistics, and determine financial growth.
The Mathematical Underpinning: Ratios, Fractions, and Proportions
The ability to calculate percentages relies on the mathematical concepts of ratios, fractions, and proportions. A ratio is simply a comparison of two numbers, often expressed as a fraction. In our case, the ratio of 45 to 60 is written as 45/60. A fraction represents a part of a whole, and it can be simplified or converted into a decimal. The fraction 45/60 can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 15. This simplifies the fraction to 3/4. A proportion is an equation stating that two ratios are equal. Percentages utilize proportions to relate a part to a whole and express it as a value out of 100.
The connection between these concepts is vital for understanding percentage calculations. By understanding the relationship between the part (45), the whole (60), and the percentage (the unknown we're trying to find), we can set up a proportion and solve for the unknown. This proportion is expressed as:
part / whole = percentage / 100
In our specific problem, this translates to:
45 / 60 = x / 100
Where 'x' represents the percentage we're trying to find. Solving for 'x' involves cross-multiplication and division, ultimately leading us to the answer.
A Brief History of Percentages
The concept of percentages has ancient roots, tracing back to the Roman Empire. As early as the reign of Augustus, the Romans used fractions that were multiples of one hundred to assess taxes on goods sold at auction. They called this centesima rerum venalium. However, the modern symbol "%" evolved much later. During the Middle Ages, as trade and commerce flourished, the need for standardized ways to calculate interest, profit margins, and taxes grew.
The use of percentages as we know them today became widespread in the 15th century. Early notations involved phrases like "per cento," which gradually evolved into abbreviations such as "p cento" and later "p. 100." Over time, the "p" was dropped, and the "cento" was contracted to a circle divided by a horizontal line, eventually morphing into the modern "%" symbol. The first known explicit use of the % symbol occurred in an Italian arithmetic text in 1425. The widespread adoption of percentages simplified complex financial calculations, contributing to the growth of banking and international trade.
The Significance of the Base: Why "Of" Matters
In percentage problems, the word "of" is critically important. It indicates the base or the whole to which the percentage is applied. Changing the base drastically alters the percentage. For instance, "what percent of 60 is 45" is very different from "what percent of 45 is 60." In the first case, 60 is the base, and we're trying to determine what proportion of that base is represented by 45. In the second case, 45 is the base, and we're determining how much larger 60 is compared to that base, expressed as a percentage.
The base is the denominator in the fraction that represents the ratio. Always carefully identify the base in a percentage problem, as it directly impacts the calculation. Failing to recognize the correct base leads to incorrect answers, potentially resulting in miscalculations in financial analyses, scientific experiments, or everyday shopping scenarios. Therefore, paying close attention to the wording of the problem and correctly identifying the base is paramount to accurate percentage calculations.
Formulas for Success: Calculating Percentages with Confidence
While the underlying concepts of ratios and proportions are essential, having a clear formula simplifies the process of calculating percentages. There are several equivalent ways to express the formula for finding what percentage one number is of another, but they all derive from the same basic principle:
Percentage = (Part / Whole) * 100
Where:
- Part is the number that represents a portion of the whole.
- Whole is the total amount or the base.
Applying this formula to our example, "what percent of 60 is 45," we have:
- Part = 45
- Whole = 60
Therefore, the percentage is:
Percentage = (45 / 60) * 100 = 0.75 * 100 = 75%
Thus, 45 is 75% of 60. Understanding and applying this formula accurately streamlines the calculation process, ensuring that you arrive at the correct answer efficiently. Memorizing this formula or keeping it handy as a reference tool significantly boosts your confidence when tackling percentage problems.
Current Trends and Insights
The use of percentages is deeply embedded in modern data analysis, statistical reporting, and everyday decision-making. Several trends highlight the continued importance and evolving applications of percentages in various fields.
Data Visualization and Infographics
In the age of information overload, data visualization has become crucial for conveying complex information quickly and effectively. Percentages are often used in charts, graphs, and infographics to represent proportions, comparisons, and trends. Pie charts, bar graphs, and stacked column charts commonly employ percentages to illustrate the distribution of data across different categories. The clarity and simplicity of percentages make them an ideal tool for presenting data to a broad audience, regardless of their statistical expertise. For instance, news articles and reports frequently use percentages to describe survey results, economic indicators, and demographic trends.
E-commerce and Marketing Analytics
E-commerce platforms and marketing professionals heavily rely on percentages to track performance metrics, analyze customer behavior, and optimize marketing campaigns. Conversion rates, click-through rates, and bounce rates are often expressed as percentages to gauge the effectiveness of website design, advertising strategies, and sales promotions. By monitoring these key performance indicators (KPIs) as percentages, businesses can identify areas for improvement and make data-driven decisions to enhance customer engagement and drive revenue growth. A/B testing, a common practice in online marketing, frequently uses percentages to compare the performance of different website versions or advertising creatives.
Financial Analysis and Investment Management
Percentages are fundamental to financial analysis and investment management. Interest rates, return on investment (ROI), profit margins, and expense ratios are all expressed as percentages to assess the profitability and risk associated with different investment opportunities. Investors use percentages to compare the performance of different stocks, bonds, and mutual funds, and to make informed decisions about portfolio allocation. Moreover, percentages are used to calculate compound interest, inflation rates, and tax liabilities, making them an indispensable tool for personal finance and wealth management.
Expert Insights: The Human Element in Percentage Interpretation
While the mathematical calculation of percentages is straightforward, interpreting and applying them effectively requires critical thinking and contextual awareness. Experts emphasize the importance of considering the sample size, potential biases, and underlying assumptions when analyzing data presented as percentages. A small sample size can lead to misleading percentages, and biases in data collection can skew results. Furthermore, understanding the context in which percentages are presented is crucial for drawing meaningful conclusions.
For example, a 50% increase in sales might seem impressive, but if the initial sales volume was very low, the absolute increase might be insignificant. Similarly, a high percentage of customer satisfaction might be less meaningful if the survey response rate was low. Experts advise readers to critically evaluate the data behind the percentages and to consider multiple sources of information before making decisions based solely on percentage values. The human element of critical interpretation is crucial for avoiding misinterpretations and making informed judgments based on percentage data.
Practical Tips and Expert Advice
Mastering percentage calculations and their applications requires more than just memorizing formulas. Here are some practical tips and expert advice to help you confidently tackle percentage-related problems in real-world scenarios:
Tip 1: Convert Percentages to Decimals for Calculations
When performing calculations involving percentages, it's often easier to convert the percentage to its decimal equivalent first. To convert a percentage to a decimal, divide it by 100. For example, 75% becomes 0.75, 150% becomes 1.5, and 0.5% becomes 0.005. This conversion simplifies multiplication and division operations, reducing the risk of errors. For instance, if you need to calculate 75% of 60, you can simply multiply 0.75 by 60, which equals 45. This approach streamlines the calculation process and makes it easier to perform mental math or use a calculator efficiently.
Tip 2: Use Proportions to Solve Complex Problems
When faced with more complex percentage problems, setting up a proportion can be a helpful strategy. A proportion is an equation that states that two ratios are equal. By identifying the known values and the unknown value, you can set up a proportion and solve for the unknown. For example, if you know that 30% of a number is 45, you can set up the proportion:
30 / 100 = 45 / x
Where 'x' represents the unknown number. Cross-multiplying gives you:
30x = 4500
Dividing both sides by 30 yields:
x = 150
Therefore, the unknown number is 150. Using proportions provides a structured approach to solving percentage problems, especially when the relationship between the part, whole, and percentage is not immediately clear.
Tip 3: Estimate and Check Your Answers
Before performing any percentage calculation, take a moment to estimate the answer. This helps you to identify potential errors and ensures that your final answer is reasonable. For example, if you're calculating 20% of 80, you know that 10% of 80 is 8, so 20% should be around 16. After calculating the exact answer, compare it to your estimate to make sure it's in the right ballpark. Estimating and checking your answers is a valuable habit that improves accuracy and prevents costly mistakes, especially in financial or scientific contexts.
Tip 4: Practice Regularly with Real-World Examples
The best way to master percentage calculations is to practice regularly with real-world examples. Look for opportunities to apply your knowledge in everyday situations, such as calculating discounts while shopping, figuring out tips at restaurants, or analyzing financial reports. The more you practice, the more comfortable and confident you'll become with percentages. Consider using online resources, textbooks, or workbooks to find practice problems and quizzes. Regular practice reinforces your understanding of the concepts and improves your ability to solve percentage problems quickly and accurately.
Tip 5: Understand Common Percentage-Related Terminology
Familiarize yourself with common percentage-related terminology, such as percentage increase, percentage decrease, percentage point, and basis point. Understanding these terms will help you to interpret data and communicate effectively in various professional and academic settings. For example, a percentage increase refers to the relative change in a quantity, while a percentage point refers to the absolute difference between two percentages. Knowing the difference between these terms is crucial for accurately interpreting data and avoiding miscommunication. A basis point, equal to one-hundredth of one percent, is commonly used in finance to express small changes in interest rates or yields.
Frequently Asked Questions (FAQ)
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator, then multiply the result by 100. For example, to convert 3/4 to a percentage: (3 / 4) * 100 = 75%. Therefore, 3/4 is equal to 75%.
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase measures the relative increase in a value, calculated as [(New Value - Old Value) / Old Value] * 100. Percentage decrease measures the relative decrease in a value, calculated as [(Old Value - New Value) / Old Value] * 100.
Q: How do I calculate a percentage discount?
A: To calculate a percentage discount, multiply the original price by the discount percentage (expressed as a decimal). Then, subtract the result from the original price. For example, if an item originally costs $80 and is 20% off, the discount is $80 * 0.20 = $16. The sale price is $80 - $16 = $64.
Q: What is a percentage point?
A: A percentage point is the unit for the arithmetic difference of two percentages. For example, if interest rates increase from 5% to 7%, that is an increase of 2 percentage points.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an original value, and the new value is more than double the original. For example, if a company's revenue increases from $100,000 to $250,000, that's a 150% increase.
Conclusion
Understanding how to calculate "what percent of 60 is 45" provides a fundamental skill applicable across various fields, from everyday shopping to complex data analysis. The answer, 75%, highlights the proportion of 45 relative to 60, expressed as a percentage. This ability to determine percentages efficiently and accurately empowers you to make informed decisions, analyze data critically, and navigate financial scenarios with confidence.
Now that you've grasped the concepts and techniques involved in percentage calculations, take the next step: put your knowledge into practice. Whether it's calculating discounts, analyzing statistics, or managing your personal finances, the more you apply these skills, the more proficient you'll become. Share this article with your friends and colleagues, and let's collectively enhance our understanding of percentages. Leave a comment below with your own examples of how you use percentage calculations in your daily life, and let's continue the conversation.
Latest Posts
Latest Posts
-
What Is Infiltration In Water Cycle
Nov 23, 2025
-
How Tall Is The Sunshine Skyway
Nov 23, 2025
-
Food Web Of A Temperate Deciduous Forest
Nov 23, 2025
-
What Is Collection In The Water Cycle
Nov 23, 2025
-
What Are The Reactants In Cellular Respiration
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.