What Percentage Of 15 Is 12
sandbardeewhy
Nov 23, 2025 · 14 min read
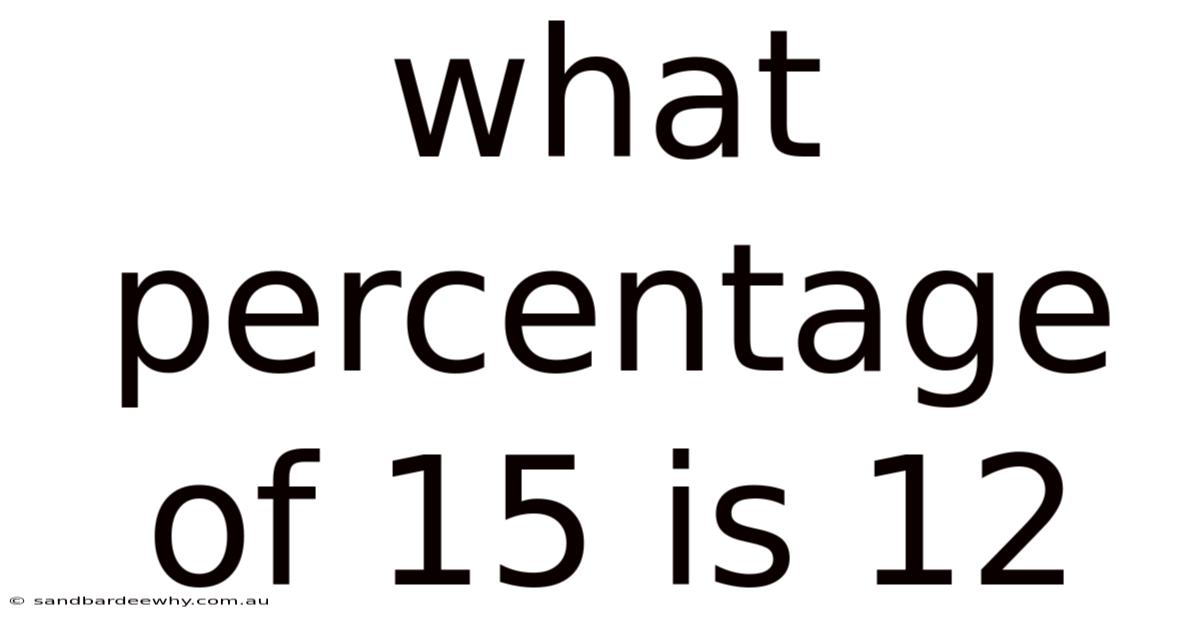
Table of Contents
Have you ever found yourself in a situation where you needed to calculate a percentage but couldn't quite figure it out? Maybe you were trying to determine the discount on a sale item or calculate your score on a test. Percentages are a fundamental part of everyday life, and understanding how to work with them is crucial. Let's say you want to know what percentage of 15 is 12. This question might seem simple, but it's important to break it down and understand the process involved.
Calculating percentages can often feel like navigating a complex maze, especially when the numbers aren't straightforward. But don't worry, it's not as difficult as it seems. We often encounter situations where we need to figure out what percentage one number represents of another. Understanding this concept not only simplifies everyday calculations but also enhances your problem-solving skills. So, how do you determine what percentage of 15 is 12? Let's dive in and explore the various methods and concepts that will help you master this essential skill.
Decoding Percentage Basics
To accurately determine what percentage of 15 is 12, it’s crucial to understand the basic concepts of percentages. A percentage is essentially a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." This means that when we say "50 percent," we are referring to 50 out of 100, or 50/100. Percentages are used to express how large one quantity is relative to another. They provide a standardized way to compare different proportions, making it easier to understand and communicate numerical relationships.
Percentages are used everywhere. They can be seen in retail discounts, financial reports, statistical data, and academic grading. For instance, when a store advertises a "20% off" sale, it means that the price of each item is reduced by 20 out of every 100 parts of the original price. In finance, interest rates are often expressed as percentages, showing the proportion of the principal that will be paid as interest over a certain period. In statistics, percentages help to convey the distribution and prevalence of data, making it easier to interpret and draw conclusions. Understanding percentages is therefore essential for making informed decisions in many areas of life.
At its core, calculating percentages involves three main components: the base, the part, and the percentage. The base is the total or whole amount, the part is a portion of that total, and the percentage is the ratio of the part to the base, expressed as a fraction of 100. In the question "What percentage of 15 is 12?", 15 is the base (the whole), 12 is the part (the portion of the whole), and we are trying to find the percentage. The formula to calculate the percentage is:
Percentage = (Part / Base) * 100
This formula tells us to divide the part by the base and then multiply the result by 100 to express the answer as a percentage. In our example, this would be:
Percentage = (12 / 15) * 100
Understanding this formula is the first step in accurately calculating percentages.
To further clarify, let's consider a different example. Suppose you have a class of 25 students, and 20 of them passed an exam. To find the percentage of students who passed, you would use the formula:
Percentage = (Number of students who passed / Total number of students) * 100
Percentage = (20 / 25) * 100
Percentage = 0.8 * 100
Percentage = 80%
This calculation shows that 80% of the students passed the exam.
Another way to think about percentages is through fractions and decimals. A percentage can be easily converted into a fraction by placing it over 100. For example, 25% is equivalent to 25/100, which simplifies to 1/4. Similarly, a percentage can be converted into a decimal by dividing it by 100. For example, 25% is equivalent to 0.25. Understanding these conversions can be helpful in simplifying calculations and visualizing proportions.
Step-by-Step Calculation: What Percentage of 15 is 12?
Now that we have covered the basics, let's apply the formula to our specific question: What percentage of 15 is 12? Here's a detailed, step-by-step breakdown:
- Identify the Base and the Part: In this case, 15 is the base (the whole), and 12 is the part (the portion of the whole we are interested in).
- Apply the Formula: Use the formula
Percentage = (Part / Base) * 100. - Plug in the Values: Substitute the values into the formula:
Percentage = (12 / 15) * 100. - Perform the Division: Divide 12 by 15:
12 / 15 = 0.8. - Multiply by 100: Multiply the result by 100 to convert it to a percentage:
0.8 * 100 = 80.
Therefore, 12 is 80% of 15. This step-by-step approach ensures accuracy and clarity in your calculations.
To reinforce this process, let's walk through another example. Suppose you want to find what percentage of 50 is 35.
- Identify the Base and the Part: Here, 50 is the base, and 35 is the part.
- Apply the Formula: Use the formula
Percentage = (Part / Base) * 100. - Plug in the Values: Substitute the values into the formula:
Percentage = (35 / 50) * 100. - Perform the Division: Divide 35 by 50:
35 / 50 = 0.7. - Multiply by 100: Multiply the result by 100 to convert it to a percentage:
0.7 * 100 = 70.
Thus, 35 is 70% of 50.
Understanding this process not only helps in solving straightforward percentage problems but also lays the foundation for tackling more complex calculations. With practice, you can easily and accurately determine percentages in a variety of situations.
Alternative Methods for Calculating Percentages
While the formula Percentage = (Part / Base) * 100 is the standard method for calculating percentages, there are alternative approaches that can be useful in different situations. These methods include using proportions, mental math techniques, and percentage calculators.
Using Proportions: A proportion is an equation that states that two ratios are equal. In the context of percentages, a proportion can be set up to relate the part to the base and the percentage to 100. For example, to find what percentage of 15 is 12, you can set up the following proportion:
12 / 15 = x / 100
Here, x represents the percentage we are trying to find. To solve for x, you can cross-multiply:
12 * 100 = 15 * x
1200 = 15x
Now, divide both sides by 15:
x = 1200 / 15
x = 80
This method yields the same result as the formula, showing that 12 is 80% of 15. Proportions can be particularly useful when dealing with more complex percentage problems or when you prefer a visual approach to solving equations.
Mental Math Techniques: For simpler percentage calculations, mental math techniques can be incredibly efficient. These techniques often involve breaking down the numbers into more manageable parts. For example, to find what percentage of 15 is 12, you can use the following approach:
- Simplify the Fraction: Reduce the fraction 12/15 to its simplest form. Both 12 and 15 are divisible by 3, so
12/15 = 4/5. - Convert to a Percentage: Recognize that 4/5 is a common fraction that is easily converted to a percentage. Since 1/5 is 20%, then 4/5 is
4 * 20% = 80%.
This mental math technique relies on recognizing common fractions and their percentage equivalents, making it a quick and easy way to calculate percentages without the need for a calculator.
Another useful mental math technique involves finding 10% of the base and then using that to find other percentages. For example, to find 20% of a number, you can first find 10% and then double it. This approach can be particularly helpful when calculating discounts or tips.
Percentage Calculators: In today's digital age, percentage calculators are readily available online and as mobile apps. These calculators can quickly and accurately determine percentages, making them a convenient tool for everyday use. To use a percentage calculator, you simply enter the base and the part, and the calculator will automatically display the percentage. While calculators are useful for quick calculations, it's still important to understand the underlying concepts and formulas to ensure that you are using the calculator correctly and interpreting the results accurately.
Each of these alternative methods offers a different approach to calculating percentages, providing you with a range of tools to choose from based on the specific situation and your personal preferences.
Common Mistakes to Avoid
Calculating percentages is a fundamental skill, but it's easy to make mistakes if you're not careful. Here are some common errors to watch out for:
- Incorrectly Identifying the Base and the Part: One of the most common mistakes is confusing the base and the part. The base is the total or whole amount, while the part is the portion of that total you're interested in. Always double-check which number represents the whole and which represents the portion. For example, in the question "What percentage of 15 is 12?", 15 is the base (the whole), and 12 is the part (the portion).
- Forgetting to Multiply by 100: After dividing the part by the base, it's crucial to multiply the result by 100 to express the answer as a percentage. Forgetting this step will give you a decimal or fraction, not a percentage.
- Rounding Errors: When dealing with decimals, rounding errors can occur if you round prematurely. It's best to perform the calculation to several decimal places and then round the final answer to the desired level of precision.
- Misinterpreting the Question: Sometimes, the wording of the question can be confusing. Make sure you understand exactly what the question is asking before you start calculating. For example, "What is 20% of 50?" is different from "What percentage of 50 is 20?"
- Relying Too Much on Calculators: While calculators are useful tools, relying on them without understanding the underlying concepts can lead to mistakes. Always double-check your answers and make sure they make sense in the context of the problem.
By being aware of these common mistakes, you can avoid errors and ensure that your percentage calculations are accurate.
To illustrate, let's consider a few examples of how these mistakes can occur and how to avoid them:
-
Example 1: Incorrectly Identifying the Base and the Part
- Problem: A student incorrectly calculates what percentage of 20 is 5 by dividing 20 by 5 and multiplying by 100, resulting in 400%.
- Solution: The student should have divided 5 (the part) by 20 (the base) and then multiplied by 100:
(5 / 20) * 100 = 25%.
-
Example 2: Forgetting to Multiply by 100
- Problem: A shopper calculates the discount on an item by dividing the discount amount by the original price but forgets to multiply by 100, resulting in a decimal value instead of a percentage.
- Solution: The shopper should have multiplied the result by 100 to express the discount as a percentage. For instance, if the discount is $10 and the original price is $50, the calculation should be
(10 / 50) * 100 = 20%.
-
Example 3: Misinterpreting the Question
- Problem: A person is asked to find what percentage of 100 is 30 but instead calculates 30% of 100.
- Solution: The person should recognize that the question is asking for the percentage that 30 represents out of 100, which is simply 30%. Calculating 30% of 100 would result in a different answer (30).
Real-World Applications
Understanding how to calculate percentages is not just an academic exercise; it has numerous practical applications in everyday life. From managing personal finances to making informed purchasing decisions, percentages play a crucial role in various scenarios.
Financial Literacy: Percentages are essential for financial literacy. When dealing with budgets, investments, loans, and taxes, understanding percentages can help you make informed decisions. For example:
- Budgeting: Calculating the percentage of your income that you spend on different categories (e.g., housing, food, transportation) can help you identify areas where you can save money.
- Investments: Understanding percentage returns on investments allows you to compare different investment options and assess their potential profitability.
- Loans: When taking out a loan, knowing the interest rate (expressed as a percentage) helps you understand the total cost of borrowing.
- Taxes: Calculating tax deductions and credits often involves percentages, helping you minimize your tax liability.
Retail and Discounts: Percentages are commonly used in retail to express discounts and sales. Being able to quickly calculate the discounted price can help you determine whether a deal is truly worthwhile. For example, if an item is advertised as "30% off," you can calculate the discount amount by multiplying the original price by 30% (or 0.30).
Health and Nutrition: Percentages are also important in health and nutrition. Nutrition labels often list the percentage of daily values for various nutrients, helping you make informed food choices. For example, if a food item contains 20% of the daily recommended intake of vitamin C, you know that it provides a significant portion of your daily needs.
Academic Performance: In academic settings, percentages are used to calculate grades and assess performance. Understanding how your scores translate into percentages can help you track your progress and identify areas where you need to improve. For example, if you score 85 out of 100 on a test, your grade is 85%.
Data Analysis: In various professional fields, percentages are used to analyze data and draw conclusions. For example, in marketing, percentages can be used to track the success of advertising campaigns. In healthcare, percentages can be used to monitor patient outcomes.
By recognizing the importance of percentages in these real-world applications, you can appreciate the value of mastering this fundamental skill.
FAQs
Q: How do I convert a percentage to a decimal? A: To convert a percentage to a decimal, divide the percentage by 100. For example, 25% is equal to 25/100, which is 0.25.
Q: How do I convert a decimal to a percentage? A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 is equal to 0.75 * 100, which is 75%.
Q: What is the difference between percent increase and percent decrease? A: Percent increase is the percentage by which a quantity has increased, while percent decrease is the percentage by which a quantity has decreased. The formulas are:
- Percent Increase =
((New Value - Original Value) / Original Value) * 100 - Percent Decrease =
((Original Value - New Value) / Original Value) * 100
Q: How do I calculate a percentage of a number? A: To calculate a percentage of a number, multiply the number by the percentage expressed as a decimal. For example, to find 20% of 50, multiply 50 by 0.20, which equals 10.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an original value, and the new value is more than double the original value. For example, if a company's revenue increases from $100,000 to $250,000, the percent increase is (($250,000 - $100,000) / $100,000) * 100 = 150%.
Conclusion
In summary, determining what percentage of 15 is 12 involves understanding the basic principles of percentages and applying the formula Percentage = (Part / Base) * 100. By identifying the base (15) and the part (12), we can calculate that 12 is 80% of 15. This calculation is not just a mathematical exercise; it's a practical skill with wide-ranging applications in finance, retail, health, academics, and various professional fields.
Mastering the calculation of percentages empowers you to make informed decisions, analyze data effectively, and solve real-world problems with confidence. Whether you're calculating discounts, managing your budget, or interpreting statistical data, a solid understanding of percentages is essential for navigating the complexities of modern life. So, embrace the power of percentages and continue to refine your skills to unlock new opportunities and achieve your goals.
Now that you have a comprehensive understanding of how to calculate percentages, put your knowledge to the test! Try solving different percentage problems and explore real-world scenarios where this skill can be applied. Share your insights and experiences in the comments below, and let's continue to learn and grow together!
Latest Posts
Latest Posts
-
What Is The Energy In Motion
Nov 23, 2025
-
How Many Pounds In 72 Kilos
Nov 23, 2025
-
5 Yards Is How Many Inches
Nov 23, 2025
-
How Many Gallons In 15 Litres
Nov 23, 2025
-
How Many Miles Per Hour Is 20 Knots
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 15 Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.