What Percentage Of 50 Is 20
sandbardeewhy
Nov 27, 2025 · 12 min read
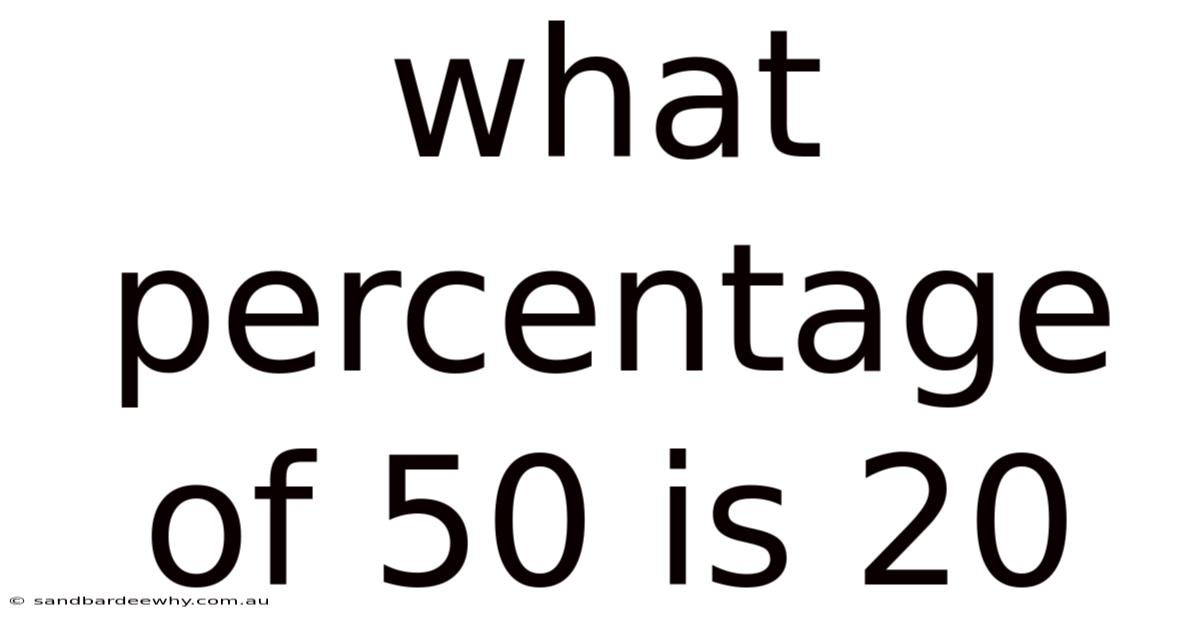
Table of Contents
Imagine you're at a store, eyeing a cool gadget. The price tag says $50, but there's a discount of $20. You quickly wonder, "What percentage off is that, really?" Understanding how to calculate percentages is more than just a math skill; it's a practical life tool that helps us make informed decisions every day, from shopping to finance.
We often encounter situations where we need to figure out what percentage one number is of another. Whether it's calculating your score on a test, figuring out a discount, or understanding financial data, knowing how to find what percentage of 50 is 20 can be incredibly useful. This article will guide you through the process, offering clear explanations, practical tips, and real-world examples to master this essential skill.
Understanding the Basics of Percentage Calculation
Percentages are a fundamental part of mathematics and are used extensively in various aspects of daily life. The concept is simple: a percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." This makes percentages an easy way to standardize comparisons, regardless of the original total.
At its core, finding what percentage of 50 is 20 involves understanding the relationship between these two numbers and expressing it as a fraction of 100. The basic formula to calculate this is:
(Part / Whole) × 100 = Percentage
Where:
- Part is the smaller amount you're comparing to the whole. In this case, it's 20.
- Whole is the total or the reference amount. Here, it's 50.
Using this formula, the calculation to find what percentage of 50 is 20 becomes straightforward:
(20 / 50) × 100 = Percentage
This calculation essentially tells us how many "parts" of 100 the number 20 represents when compared to the number 50.
Understanding this basic principle is crucial because it forms the foundation for more complex percentage calculations. Whether you're dealing with discounts, interest rates, statistics, or proportions, the underlying concept remains the same. By mastering this simple formula, you can confidently tackle a wide range of mathematical problems encountered in both academic and real-world scenarios.
A Brief History of Percentages
The use of percentages can be traced back to ancient Rome. As the Roman Empire expanded, the need for standardized financial calculations grew. The Romans often used fractions like 1/100 to calculate taxes on goods sold at auction. This practice gradually evolved, and by the Middle Ages, the concept of calculating percentages had become more refined.
During the Renaissance, with the rise of trade and commerce, percentages became increasingly important. Merchants needed a standardized way to calculate profits, losses, and interest rates. This led to the widespread adoption of percentage calculations in Europe. The symbol "%" evolved from the Italian term per cento, which means "for each hundred." Over time, the term was abbreviated, and the symbol we use today became commonplace.
The formalization of percentages was further aided by the development of the decimal system. Decimal fractions made it easier to perform percentage calculations accurately. As mathematics advanced, percentages became an integral part of various fields, including finance, statistics, and science. Today, percentages are used globally in countless applications, making them an indispensable tool for understanding and interpreting numerical data.
Essential Concepts and Terminology
To fully grasp percentage calculations, it's essential to understand some key concepts and terminology:
- Base: The base, or whole, is the total amount or reference point to which the percentage is applied. In our example, 50 is the base.
- Rate: The rate is the percentage itself, often expressed with the "%" symbol. It represents the proportion of the base that is being considered.
- Percentage (Amount): This is the result of applying the rate to the base. It's the actual amount that the percentage represents. In our example, 20 is the percentage amount.
It's also crucial to distinguish between percentage increase and percentage decrease. A percentage increase occurs when a quantity increases, and the percentage is calculated to show the extent of the increase relative to the original amount. Conversely, a percentage decrease occurs when a quantity decreases, and the percentage is calculated to show the extent of the decrease relative to the original amount.
For example, if a price increases from $50 to $60, the percentage increase is calculated as follows:
[(New Value - Original Value) / Original Value] × 100 [(60 - 50) / 50] × 100 = 20%
Similarly, if a price decreases from $50 to $40, the percentage decrease is calculated as follows:
[(Original Value - New Value) / Original Value] × 100 [(50 - 40) / 50] × 100 = 20%
These concepts are fundamental for understanding financial calculations, statistical analysis, and various other applications.
Practical Applications of Percentage Calculations
Percentage calculations are not just theoretical exercises; they have numerous practical applications in everyday life. Here are a few examples:
- Retail Discounts: Stores often offer discounts as a percentage of the original price. Understanding how to calculate these percentages helps you determine the actual savings and make informed purchasing decisions.
- Financial Investments: Interest rates on loans and investments are expressed as percentages. Calculating these percentages allows you to compare different financial products and understand the potential returns or costs.
- Statistical Analysis: Percentages are used to present data in a clear and understandable format. For example, election results, survey responses, and market share are often expressed as percentages.
- Health and Nutrition: Nutritional information on food labels often includes percentages of daily recommended values. These percentages help you make informed choices about your diet.
- Academic Grading: Test scores and grades are frequently expressed as percentages. Understanding how these percentages are calculated helps you track your academic progress.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, there are some common mistakes to avoid:
- Misidentifying the Base: One of the most common errors is using the wrong number as the base. Always make sure to identify the total amount or reference point correctly.
- Incorrectly Applying the Formula: Ensure that you are using the correct formula (Part / Whole) × 100. Mixing up the part and whole will result in an incorrect percentage.
- Ignoring Context: Pay attention to the context of the problem. For example, when calculating percentage increase or decrease, make sure to use the original value as the base.
- Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple calculations. Rounding too early can lead to significant inaccuracies.
By understanding these common mistakes and taking steps to avoid them, you can improve the accuracy of your percentage calculations.
Trends and Latest Developments
In today's data-driven world, the use of percentages is more prevalent than ever. Businesses, governments, and individuals rely on percentages to analyze trends, make decisions, and communicate information effectively. Several recent trends and developments highlight the ongoing importance of percentage calculations.
Data Visualization: With the rise of big data, data visualization tools have become essential for presenting complex information in an accessible format. Percentages play a crucial role in these visualizations, allowing users to quickly understand proportions and comparisons. Charts, graphs, and dashboards often use percentages to highlight key trends and patterns.
E-commerce and Retail: The e-commerce industry heavily relies on percentage calculations for pricing, discounts, and marketing campaigns. Dynamic pricing strategies often involve calculating percentage markups or markdowns based on market demand and competitor pricing. Retailers also use percentages to track sales performance, inventory levels, and customer behavior.
Financial Technology (FinTech): FinTech companies use percentages extensively in various applications, including loan calculations, investment analysis, and risk management. Algorithmic trading platforms often use percentage-based strategies to execute trades automatically. Personal finance apps use percentages to help users track their spending, savings, and investment returns.
Healthcare Analytics: In healthcare, percentages are used to analyze patient outcomes, track disease prevalence, and evaluate the effectiveness of treatments. Public health organizations use percentages to monitor vaccination rates, infection rates, and other key health indicators.
Social Media Analytics: Social media platforms use percentages to measure user engagement, track campaign performance, and analyze audience demographics. Metrics such as click-through rates, conversion rates, and follower growth are often expressed as percentages.
These trends demonstrate the continued relevance of percentage calculations in various industries and highlight the need for individuals to develop strong mathematical literacy skills.
Tips and Expert Advice
Calculating percentages can be made easier and more accurate with a few practical tips and expert advice:
-
Understand the Question:
- Before diving into calculations, make sure you fully understand what the question is asking. Are you trying to find what percentage one number is of another, calculate a percentage increase or decrease, or determine a discounted price? Misinterpreting the question can lead to incorrect calculations.
- For example, if the question is "What percentage of 50 is 20?" you know that 50 is the base (whole) and 20 is the part. This understanding will guide your calculation process.
-
Use a Calculator or Spreadsheet:
- While it's good to understand the underlying math, using a calculator or spreadsheet can significantly reduce the risk of errors, especially when dealing with complex numbers.
- Spreadsheet programs like Microsoft Excel or Google Sheets allow you to create formulas that automatically calculate percentages. This can be particularly useful for repetitive tasks or when dealing with large datasets. For example, in Excel, you can calculate what percentage of 50 is 20 by entering the formula
=20/50*100into a cell.
-
Double-Check Your Work:
- Always double-check your calculations to ensure accuracy. It's easy to make a mistake, especially when performing multiple steps.
- One way to double-check is to use estimation. For example, if you calculate that 20 is 40% of 50, quickly estimate to see if that seems reasonable. In this case, 50% of 50 would be 25, so 40% being 20 makes sense.
-
Convert to Decimal Form:
- Converting percentages to decimal form can simplify calculations, especially when dealing with more complex problems.
- To convert a percentage to a decimal, divide it by 100. For example, 40% becomes 0.40. You can then use this decimal value in calculations. For instance, to find 40% of 50, multiply 50 by 0.40, which equals 20.
-
Use Percentage Increase/Decrease Formulas Correctly:
- When calculating percentage increases or decreases, make sure to use the correct formula and identify the original value accurately.
- The formula for percentage increase is
[(New Value - Original Value) / Original Value] × 100, and the formula for percentage decrease is[(Original Value - New Value) / Original Value] × 100. For example, if a price increases from $50 to $75, the percentage increase is[(75 - 50) / 50] × 100 = 50%.
-
Practice Regularly:
- Like any skill, proficiency in percentage calculations comes with practice. Work through various examples and real-world problems to build your confidence.
- Online resources, textbooks, and math apps can provide plenty of practice problems. Start with simple calculations and gradually move on to more complex scenarios.
-
Break Down Complex Problems:
- If you encounter a complex problem involving multiple percentage calculations, break it down into smaller, more manageable steps.
- For example, if you need to calculate a series of discounts and taxes, calculate each one separately and then combine the results. This approach reduces the risk of errors and makes the problem easier to understand.
-
Use Online Tools:
- There are numerous online percentage calculators and tools available that can help you quickly and accurately perform percentage calculations.
- These tools can be particularly useful for verifying your own calculations or for handling more complex scenarios. Simply enter the values into the tool, and it will provide the result instantly.
By following these tips and seeking expert advice when needed, you can improve your accuracy and confidence in calculating percentages.
FAQ
Q: What is the formula for calculating what percentage one number is of another? A: The formula is (Part / Whole) × 100 = Percentage.
Q: How do I calculate a percentage increase? A: Use the formula [(New Value - Original Value) / Original Value] × 100.
Q: What is the difference between percentage increase and percentage decrease? A: Percentage increase is when a value goes up, while percentage decrease is when a value goes down, both calculated relative to the original value.
Q: How can I convert a percentage to a decimal? A: Divide the percentage by 100. For example, 25% becomes 0.25.
Q: Why are percentages useful in real life? A: Percentages help standardize comparisons, understand discounts, calculate interest, and interpret statistical data, making them essential for informed decision-making.
Q: What's a common mistake to avoid when calculating percentages? A: Misidentifying the base (the whole amount) is a common error. Always ensure you're using the correct reference point.
Conclusion
Understanding what percentage of 50 is 20, or any percentage calculation, is an invaluable skill with wide-ranging applications. By mastering the basic formula (Part / Whole) × 100, you can confidently tackle various real-world scenarios, from calculating discounts to interpreting financial data. Remember, 20 is 40% of 50, a calculation that underscores the importance of grasping these fundamental concepts.
Now that you have a solid understanding of percentage calculations, it's time to put your knowledge into practice. Start by identifying situations in your daily life where you can apply these skills. Whether it's calculating a tip at a restaurant, figuring out the savings on a sale item, or understanding the performance of your investments, the ability to calculate percentages will empower you to make more informed decisions.
To further enhance your understanding, consider exploring online resources, practicing with different examples, and seeking feedback from peers or mentors. The more you practice, the more confident you'll become in your ability to perform percentage calculations accurately and efficiently.
Take the next step and challenge yourself to use percentages in your daily activities. Share your experiences and insights with others, and encourage them to develop their mathematical literacy as well. By working together, we can create a more mathematically savvy society.
Latest Posts
Latest Posts
-
How Tall Is 5 2 In Meters
Nov 27, 2025
-
How Many Dry Quarts In A Gallon
Nov 27, 2025
-
What Is 3 Qt Of Water
Nov 27, 2025
-
What Is A Credibility Statement In A Speech
Nov 27, 2025
-
How Many 8 Ounce Cups In A Gallon
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 50 Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.