Which Is More 2 3 Or 3 4
sandbardeewhy
Nov 28, 2025 · 12 min read
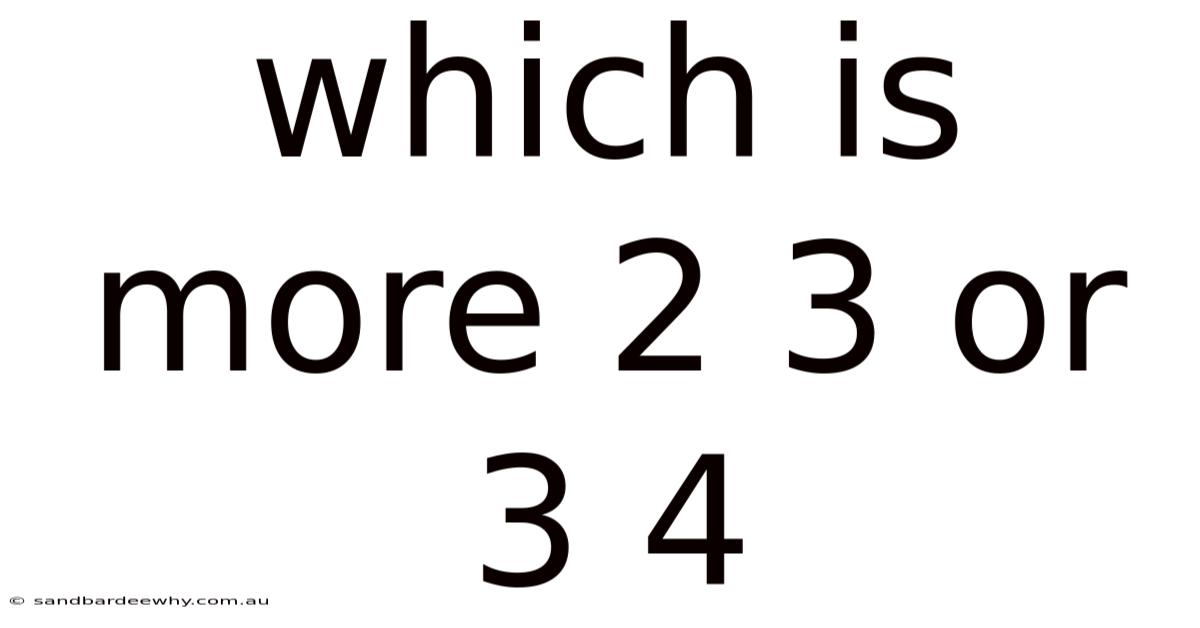
Table of Contents
Imagine you're sharing a pizza with friends. Would you rather have two slices out of a pizza cut into three pieces, or three slices from a pizza cut into four? This simple analogy helps illustrate a fundamental concept in mathematics: comparing fractions. Understanding which fraction is larger—whether it’s 2/3 or 3/4—is a skill that extends far beyond pizza slices. It's essential for everyday decision-making, from cooking and budgeting to understanding scientific data and investment opportunities.
Deciding 'which is more, 2/3 or 3/4' might seem straightforward, but it touches on important mathematical principles and techniques. Both fractions represent parts of a whole, but the difference lies in how that whole is divided. This article will delve into the nuances of comparing these fractions, providing you with a clear understanding of the underlying concepts and practical methods to confidently determine which fraction holds greater value. From understanding the basics of fractions to exploring real-world applications, we’ll cover everything you need to master this essential skill.
Main Subheading: Understanding Fractions
Fractions are a cornerstone of mathematics, representing a part of a whole. A fraction consists of two main components: the numerator and the denominator. The numerator (the top number) indicates how many parts of the whole we have, while the denominator (the bottom number) indicates the total number of equal parts into which the whole is divided.
In the fraction 2/3, the numerator is 2 and the denominator is 3. This means we have two parts out of a whole that has been divided into three equal parts. Similarly, in the fraction 3/4, the numerator is 3 and the denominator is 4, indicating that we have three parts out of a whole divided into four equal parts. Understanding this basic structure is crucial for comparing fractions and grasping their relative sizes.
Comprehensive Overview
Defining Fractions
At its core, a fraction represents a division. The fraction a/b can be understood as a divided by b. This definition is critical because it links fractions to other mathematical concepts such as ratios and proportions. Fractions can represent anything from parts of a physical object, like a pie, to ratios in a scientific experiment or probabilities in statistics.
Fractions are classified into several types, including proper fractions, improper fractions, and mixed numbers. A proper fraction has a numerator smaller than its denominator (e.g., 2/3), indicating a value less than one. An improper fraction has a numerator greater than or equal to its denominator (e.g., 5/4), indicating a value greater than or equal to one. A mixed number combines a whole number with a proper fraction (e.g., 1 1/4), representing a quantity that includes both a whole and a fractional part.
Scientific Foundations
The scientific foundations of fractions lie in their ability to quantify and represent continuous quantities. Unlike integers, which are discrete and countable, fractions allow us to express values that fall between whole numbers. This is essential in fields like physics and engineering, where measurements often involve fractional values.
For example, when measuring the length of an object, we might find that it is 2.5 meters long. This decimal value can be expressed as the fraction 5/2, providing a precise representation of the measurement. In chemistry, fractions are used to represent the molar ratios of reactants in a chemical reaction. Understanding fractions is therefore crucial for accurately representing and manipulating scientific data.
Historical Context
The concept of fractions dates back to ancient civilizations. Egyptians used fractions as early as 3000 BC, primarily to deal with practical problems such as land surveying and construction. The Egyptians had a unique system of fractions based on unit fractions, where the numerator was always 1 (e.g., 1/2, 1/3, 1/4). They would express other fractions as sums of these unit fractions.
The Babylonians developed a more sophisticated system of fractions based on the number 60, which is still reflected in our modern system of measuring time and angles (e.g., 60 seconds in a minute, 360 degrees in a circle). The Greeks further advanced the theory of fractions, with mathematicians like Euclid including discussions of fractions in their works.
The modern notation for fractions, with a horizontal line separating the numerator and denominator, became widespread during the medieval period. The Indian mathematician Aryabhata is credited with using a similar notation as early as the 5th century AD. The introduction of fractions into Europe via Arabic texts during the Middle Ages played a crucial role in the development of algebra and other advanced mathematical fields.
Essential Concepts for Comparing Fractions
To accurately determine which is more, 2/3 or 3/4, several key concepts need to be understood. These concepts provide the foundation for comparing any two fractions, regardless of their numerators and denominators.
-
Common Denominator: One of the most straightforward methods for comparing fractions is to find a common denominator. This involves finding a number that is a multiple of both denominators. Once the fractions have the same denominator, you can directly compare their numerators; the fraction with the larger numerator is the larger fraction.
-
Cross Multiplication: Cross multiplication is a quick method to compare two fractions. For fractions a/b and c/d, multiply a by d and b by c. If a * d is greater than b * c, then a/b is greater than c/d.
-
Decimal Conversion: Another approach is to convert each fraction to its decimal equivalent. This can be done by dividing the numerator by the denominator. Once the fractions are in decimal form, they can be easily compared.
-
Benchmarking: Benchmarking involves comparing both fractions to a common benchmark, such as 1/2 or 1. This is useful when the fractions are close to these benchmarks.
Detailed Comparison: 2/3 vs. 3/4
Let's apply these concepts to the specific fractions in question: 2/3 and 3/4.
-
Common Denominator: The least common multiple (LCM) of 3 and 4 is 12. Convert both fractions to have this denominator:
- 2/3 = (2 * 4) / (3 * 4) = 8/12
- 3/4 = (3 * 3) / (4 * 3) = 9/12
Since 9/12 is greater than 8/12, we conclude that 3/4 is greater than 2/3.
-
Cross Multiplication:
- 2/3 vs. 3/4
- 2 * 4 = 8
- 3 * 3 = 9
Since 9 is greater than 8, 3/4 is greater than 2/3.
-
Decimal Conversion:
- 2/3 ≈ 0.6667
- 3/4 = 0.75
Since 0.75 is greater than 0.6667, 3/4 is greater than 2/3.
-
Benchmarking:
- Both fractions are greater than 1/2. 2/3 is 1/6 away from 1, while 3/4 is 1/4 away from 1. Since 1/4 is less than 1/6, 3/4 is closer to 1, and therefore greater than 2/3.
Using all these methods, it is clear that 3/4 is greater than 2/3.
Trends and Latest Developments
Current Trends in Mathematics Education
In mathematics education, there is a growing emphasis on conceptual understanding over rote memorization. This trend encourages students to deeply understand the principles underlying mathematical operations, rather than simply memorizing formulas and procedures. For fractions, this means focusing on the meaning of the numerator and denominator and the relationships between fractions, decimals, and percentages.
Another trend is the integration of technology in mathematics education. Interactive software, online simulations, and educational apps are increasingly used to help students visualize and manipulate fractions. These tools can make abstract concepts more concrete and engaging, improving students' understanding and retention.
Data and Popular Opinions
Recent studies in mathematics education have shown that many students struggle with fractions, particularly when it comes to comparing and ordering them. A common misconception is to compare the numerators and denominators separately, without considering their relative values. For example, some students might incorrectly assume that 3/5 is greater than 2/3 because both the numerator and denominator are larger in 3/5.
Popular opinion often reflects this confusion, with many adults admitting that they find fractions challenging. This highlights the need for effective teaching strategies and resources to help students develop a solid understanding of fractions.
Professional Insights
From a professional perspective, a strong understanding of fractions is essential for success in many fields. Engineers, scientists, financial analysts, and even chefs rely on fractions to perform calculations and make informed decisions. The ability to quickly and accurately compare fractions is a valuable skill in these professions.
Moreover, fractions serve as a foundation for more advanced mathematical concepts, such as algebra and calculus. A solid understanding of fractions is therefore crucial for students pursuing careers in STEM fields.
Tips and Expert Advice
Practical Tips for Comparing Fractions
Comparing fractions can be made easier with a few practical tips:
-
Visualize Fractions: Use diagrams or visual aids to represent fractions. For example, draw two circles of the same size and divide one into three equal parts and shade two of them (representing 2/3). Divide the other circle into four equal parts and shade three of them (representing 3/4). Visually comparing the shaded areas can help you see which fraction is larger.
-
Use Real-World Examples: Relate fractions to real-world scenarios. For example, if you're comparing 2/3 of a pizza to 3/4 of a pizza, imagine cutting two identical pizzas into the respective fractions. Which would give you more pizza? This makes the concept more tangible and easier to understand.
-
Practice Regularly: Like any mathematical skill, proficiency in comparing fractions requires regular practice. Work through a variety of problems, starting with simple fractions and gradually moving on to more complex ones. Use online resources, textbooks, or worksheets to find practice problems.
Expert Advice
-
Understand the Underlying Concepts: Don't just memorize rules for comparing fractions. Make sure you understand the meaning of the numerator and denominator and how they relate to each other. This will help you solve problems more effectively and avoid common mistakes.
-
Estimate First: Before applying any specific method, try to estimate which fraction is larger. This can help you catch errors and develop a better intuition for fractions. For example, if you're comparing 7/12 and 4/7, notice that 7/12 is slightly more than 1/2, while 4/7 is slightly less than 1/2. This tells you that 7/12 is likely larger.
-
Use Technology Wisely: While technology can be a valuable tool, don't rely on it exclusively. Make sure you can compare fractions manually before using calculators or software. This will help you develop a deeper understanding of the concepts.
Real-World Examples
-
Cooking: When following a recipe, you may need to adjust ingredient quantities. For example, if a recipe calls for 2/3 cup of flour but you want to make half the recipe, you'll need to calculate half of 2/3.
-
Finance: When investing, you may need to compare the returns of different investments. If one investment yields 3/4 of a percent and another yields 5/8 of a percent, you'll need to compare these fractions to determine which investment is more profitable.
-
Construction: In construction, precise measurements are essential. If you're cutting a piece of wood, you may need to compare fractions to ensure that it is the correct size.
-
Healthcare: Doctors and nurses often use fractions to calculate medication dosages. Accurate calculations are critical to ensure patient safety.
FAQ
Q: Why is finding a common denominator important when comparing fractions?
A: Finding a common denominator allows you to compare fractions directly because it ensures that both fractions are expressed in terms of the same-sized parts of a whole. Once the denominators are the same, you can simply compare the numerators to determine which fraction is larger.
Q: Can cross multiplication always be used to compare fractions?
A: Yes, cross multiplication is a reliable method for comparing any two fractions. However, it's important to remember the correct procedure: multiply the numerator of the first fraction by the denominator of the second fraction and compare it to the product of the denominator of the first fraction and the numerator of the second fraction.
Q: Is it always necessary to find the least common denominator?
A: No, any common denominator will work, but using the least common denominator (LCD) simplifies the fractions and makes the comparison easier. If you use a larger common denominator, you'll still get the correct answer, but you may need to simplify the resulting fractions.
Q: How do you compare mixed numbers?
A: To compare mixed numbers, first compare the whole number parts. If the whole numbers are different, the mixed number with the larger whole number is the larger mixed number. If the whole numbers are the same, compare the fractional parts using any of the methods described above.
Q: What are some common mistakes to avoid when comparing fractions?
A: Common mistakes include comparing numerators or denominators separately without finding a common denominator, forgetting to simplify fractions before comparing them, and making errors in arithmetic when finding common denominators or cross-multiplying.
Conclusion
In summary, determining which is more, 2/3 or 3/4, involves understanding the fundamental concepts of fractions and applying various comparison methods such as finding a common denominator, cross multiplication, or decimal conversion. Through these methods, it becomes clear that 3/4 is greater than 2/3. Mastering the art of comparing fractions is not only a valuable mathematical skill but also a practical tool for everyday decision-making.
Now that you have a comprehensive understanding of how to compare fractions, put your knowledge to the test! Try solving various fraction comparison problems and explore real-world applications to solidify your skills. Share this article with friends and family to help them master fractions too. Leave a comment below with any questions or insights you've gained from this article, and let's continue the conversation.
Latest Posts
Latest Posts
-
How Many Ounces In A 5 Liter
Nov 28, 2025
-
How Does Place Affect The Setting Of A Story
Nov 28, 2025
-
The Sinners In The Hands Of An Angry God Summary
Nov 28, 2025
-
Domain And Range Of Piecewise Functions
Nov 28, 2025
-
What Is A Selectively Permeable Membrane
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about Which Is More 2 3 Or 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.