11 As A Percentage Of 25
sandbardeewhy
Nov 24, 2025 · 10 min read
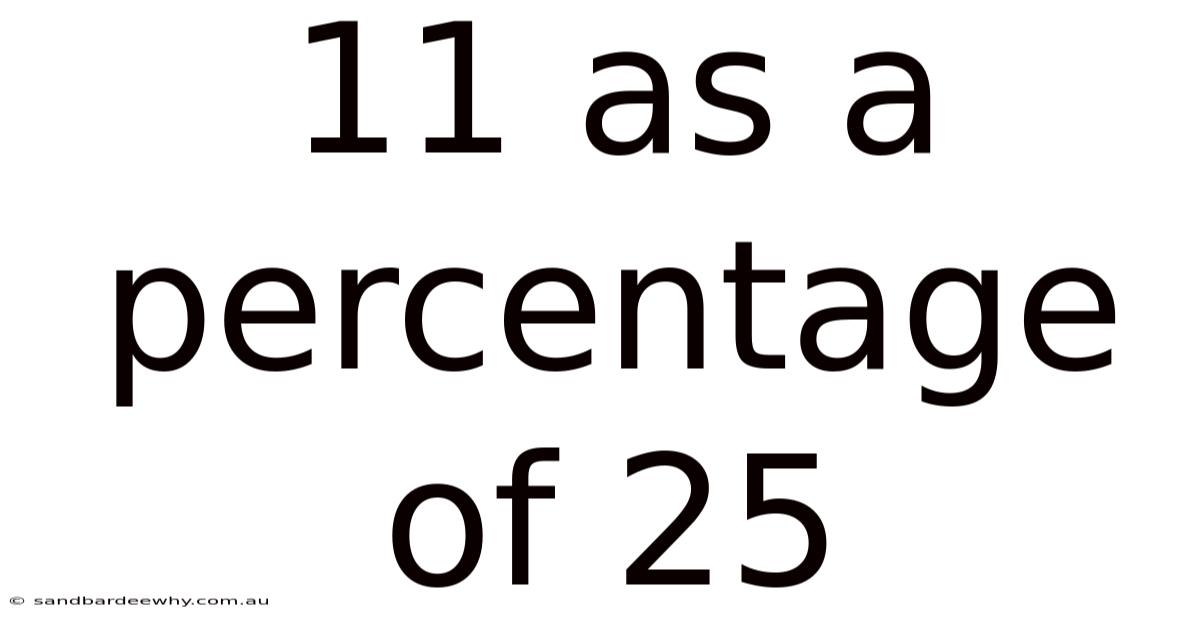
Table of Contents
Imagine you're at a local farmers market, eyeing a beautiful basket of 25 ripe, juicy strawberries. The vendor tells you that 11 of these strawberries are from a special, organic patch known for its exceptional sweetness. You might wonder, "What portion of this whole basket are these special strawberries?" That's where percentages come in handy, helping us express proportions in a way that's easy to understand and compare.
Calculating a percentage is a fundamental skill with applications far beyond the farmers market. From figuring out discounts at your favorite store to understanding financial reports, percentages are woven into the fabric of our daily lives. This article will provide a comprehensive guide to understanding how to calculate "11 as a percentage of 25," along with practical examples and insights to solidify your understanding.
Understanding the Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Essentially, when we say "X percent," we mean "X out of 100." This provides a standardized way to compare different quantities and proportions, regardless of their actual size.
Percentages are denoted by the symbol "%". So, 50% means 50 out of 100, which is equivalent to the fraction 1/2 or the decimal 0.5. This simple concept is surprisingly powerful, allowing us to represent a part of a whole in a relatable and easily understandable manner. Think about exam scores – a score of 80% immediately tells you that you answered 80 out of every 100 questions correctly.
The Formula for Calculating Percentages
At its core, calculating a percentage involves a straightforward formula:
Percentage = (Part / Whole) * 100
Where:
- Part is the specific quantity you're interested in expressing as a percentage.
- Whole is the total quantity, or the reference point to which the part is being compared.
This formula essentially calculates the fraction that the "part" represents of the "whole" and then multiplies it by 100 to express it as a percentage. Let's break this down with an example. If you have 20 apples and 5 of them are green, then:
- Part = 5 (the number of green apples)
- Whole = 20 (the total number of apples)
Therefore, the percentage of green apples is (5/20) * 100 = 25%. This means 25% of your apples are green.
Why Percentages Matter
Percentages provide a standardized way to compare and interpret data across different scales. Imagine trying to compare a salary increase of $5,000 at two different companies. At first glance, $5,000 seems like a good raise, but if one company pays a starting salary of $50,000 and the other pays $100,000, the impact of that raise is significantly different.
By expressing the raise as a percentage, we can easily compare the relative increase. A $5,000 raise on a $50,000 salary is a 10% increase, while a $5,000 raise on a $100,000 salary is only a 5% increase. This highlights the power of percentages in providing context and enabling meaningful comparisons.
Furthermore, percentages are essential in various fields, including finance (interest rates, investment returns), statistics (data analysis), retail (discounts, markups), and science (error margins). Understanding percentages empowers you to make informed decisions, interpret data accurately, and navigate the complexities of the world around you.
Converting Percentages to Decimals and Fractions
Percentages, decimals, and fractions are all interconnected ways of representing proportions. Knowing how to convert between them is crucial for mathematical operations and data interpretation.
- Percentage to Decimal: To convert a percentage to a decimal, divide the percentage by 100. For example, 75% becomes 75/100 = 0.75.
- Decimal to Percentage: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.3 becomes 0.3 * 100 = 30%.
- Percentage to Fraction: To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100 and simplify. For example, 40% becomes 40/100, which simplifies to 2/5.
- Fraction to Percentage: To convert a fraction to a percentage, divide the numerator by the denominator and multiply by 100. For example, 1/4 becomes (1/4) * 100 = 25%.
These conversions are fundamental tools for working with percentages and understanding their relationship to other numerical representations.
Common Mistakes to Avoid
When working with percentages, it's easy to fall into common traps. Here are a few to watch out for:
- Confusing the Part and the Whole: Always double-check that you're using the correct values for the "part" and the "whole" in the formula. Mixing them up will lead to inaccurate results.
- Forgetting to Multiply by 100: This is a critical step in converting the fraction to a percentage. Omitting it will give you a decimal value instead of a percentage.
- Misinterpreting Percentage Increase/Decrease: Be mindful of the base value when calculating percentage changes. For instance, a 50% decrease followed by a 50% increase does not bring you back to the original value.
By understanding the fundamentals of percentages and avoiding these common pitfalls, you'll be well-equipped to confidently tackle a wide range of percentage-related calculations.
Calculating 11 as a Percentage of 25: A Step-by-Step Guide
Now, let's apply the principles we've discussed to our specific problem: calculating 11 as a percentage of 25.
-
Identify the Part and the Whole: In this case, 11 is the "part" (the specific quantity we're interested in), and 25 is the "whole" (the total quantity).
-
Apply the Formula: Using the formula Percentage = (Part / Whole) * 100, we have:
Percentage = (11 / 25) * 100
-
Perform the Division: Divide 11 by 25:
11 / 25 = 0.44
-
Multiply by 100: Multiply the result by 100 to express it as a percentage:
- 44 * 100 = 44
Therefore, 11 as a percentage of 25 is 44%. This means that 11 represents 44 out of every 100 units in a quantity of 25.
Practical Examples and Applications
To further illustrate the concept, let's explore some real-world examples where calculating "11 as a percentage of 25" might be relevant:
- Exam Scores: Imagine a student scores 11 out of 25 on a quiz. Their score is 44%. This gives them (and their teacher) an immediate understanding of their performance.
- Inventory Management: A store has 25 items in stock, and 11 of them are a particular model. This model represents 44% of their current inventory.
- Resource Allocation: A project team has a budget of $25,000, and $11,000 is allocated to marketing. Marketing receives 44% of the total budget.
- Survey Results: In a survey of 25 people, 11 people chose a specific option. That option was favored by 44% of the respondents.
These examples demonstrate how understanding "11 as a percentage of 25" can provide valuable insights in various scenarios, allowing for informed decision-making and a clearer understanding of proportions.
Using Calculators and Tools
While the calculation is relatively simple, calculators and online tools can be helpful for quick and accurate results, especially when dealing with more complex numbers. Most basic calculators have a percentage function, and numerous online percentage calculators are readily available. These tools can save time and reduce the risk of errors. However, it's still essential to understand the underlying principles so you can interpret the results correctly.
Trends and Latest Developments
While the core concept of percentages remains unchanged, their application and interpretation are constantly evolving with the rise of data science and analytics. Here are some trends and developments:
- Data Visualization: Percentages are increasingly used in data visualizations to communicate insights effectively. Charts and graphs often display percentages to highlight proportions and trends in data sets.
- Personalized Finance: Financial technology (FinTech) apps use percentages to help users track their spending, savings, and investment performance. These tools provide personalized insights based on percentage-based analysis.
- E-commerce Analytics: Online retailers use percentages to analyze website traffic, conversion rates, and customer behavior. Understanding these metrics helps them optimize their websites and marketing campaigns.
- Public Health: Percentages are crucial in public health for tracking disease prevalence, vaccination rates, and health outcomes. This data informs public health policies and interventions.
- Machine Learning: Percentages are used in machine learning to evaluate model performance. Metrics like accuracy, precision, and recall are often expressed as percentages.
These trends highlight the continued importance of percentages in a data-driven world. As data becomes increasingly prevalent, the ability to calculate, interpret, and communicate percentages effectively will become even more valuable.
Tips and Expert Advice
Here's some practical advice to help you master the art of working with percentages:
- Practice Regularly: The more you practice calculating percentages, the more comfortable you'll become with the process. Try working through various examples and real-world scenarios.
- Estimate Before Calculating: Before using a calculator, try to estimate the percentage mentally. This will help you develop a better intuition for percentages and catch any obvious errors. For example, you might estimate that 11 out of 25 is close to 10 out of 25, which is 40%.
- Use Percentages to Compare: One of the most powerful uses of percentages is to compare different quantities or proportions. When comparing percentages, always make sure they are based on the same "whole" or reference point.
- Understand Percentage Change: When dealing with percentage increases or decreases, pay close attention to the base value. A percentage change is always calculated relative to the original value. For instance, if a price increases from $20 to $25, the percentage increase is (5/20) * 100 = 25%.
- Be Aware of Context: The interpretation of a percentage depends heavily on the context. A 5% increase in sales might be considered excellent in a mature market but disappointing in a rapidly growing one.
- Double-Check Your Work: Always double-check your calculations, especially when dealing with important financial or statistical data. A small error in a percentage calculation can have significant consequences.
By following these tips and seeking expert advice when needed, you can confidently and accurately use percentages in your daily life and professional endeavors.
FAQ
Q: What is the difference between a percentage and a percentile?
A: A percentage expresses a proportion out of 100, while a percentile indicates the value below which a given percentage of observations in a group of observations fall. For example, if you score in the 80th percentile on a test, it means you scored higher than 80% of the other test-takers.
Q: How do I calculate a percentage increase or decrease?
A: Percentage Change = ((New Value - Old Value) / Old Value) * 100. A positive result indicates an increase, while a negative result indicates a decrease.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100% when dealing with increases or changes relative to an original value. For example, if a company's revenue doubles, that's a 100% increase. If it triples, that's a 200% increase.
Q: How do I calculate the original value if I know the percentage increase and the new value?
A: Original Value = New Value / (1 + (Percentage Increase / 100)).
Q: What are some common applications of percentages in finance?
A: Percentages are used extensively in finance to calculate interest rates, investment returns, profit margins, and tax rates. They are also used to express changes in stock prices and other financial indicators.
Conclusion
In summary, calculating "11 as a percentage of 25" involves a straightforward application of the percentage formula: (Part / Whole) * 100. By identifying the "part" (11) and the "whole" (25) and performing the calculation, we arrive at the answer: 44%. Understanding this simple calculation unlocks a powerful tool for interpreting data, making informed decisions, and navigating the world around us.
From interpreting exam scores to analyzing financial data, percentages play a vital role in our daily lives. By mastering the fundamentals of percentages and practicing their application in various scenarios, you can gain a valuable skill that will serve you well in both personal and professional contexts.
Now that you have a solid understanding of how to calculate percentages, put your knowledge to the test! Try applying the formula to different scenarios and see how percentages can help you make sense of the world around you. Don't hesitate to share your findings or ask any further questions in the comments below.
Latest Posts
Latest Posts
-
Is A Meter Bigger Than A Kilometer
Nov 24, 2025
-
Difference Between A Want And Need
Nov 24, 2025
-
Who Is The Killer In And There Were None
Nov 24, 2025
-
11 As A Percentage Of 25
Nov 24, 2025
-
How Does Cytokinesis Differ In Animal And Plant Cells
Nov 24, 2025
Related Post
Thank you for visiting our website which covers about 11 As A Percentage Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.