12 Is What Percent Of 30
sandbardeewhy
Nov 23, 2025 · 10 min read
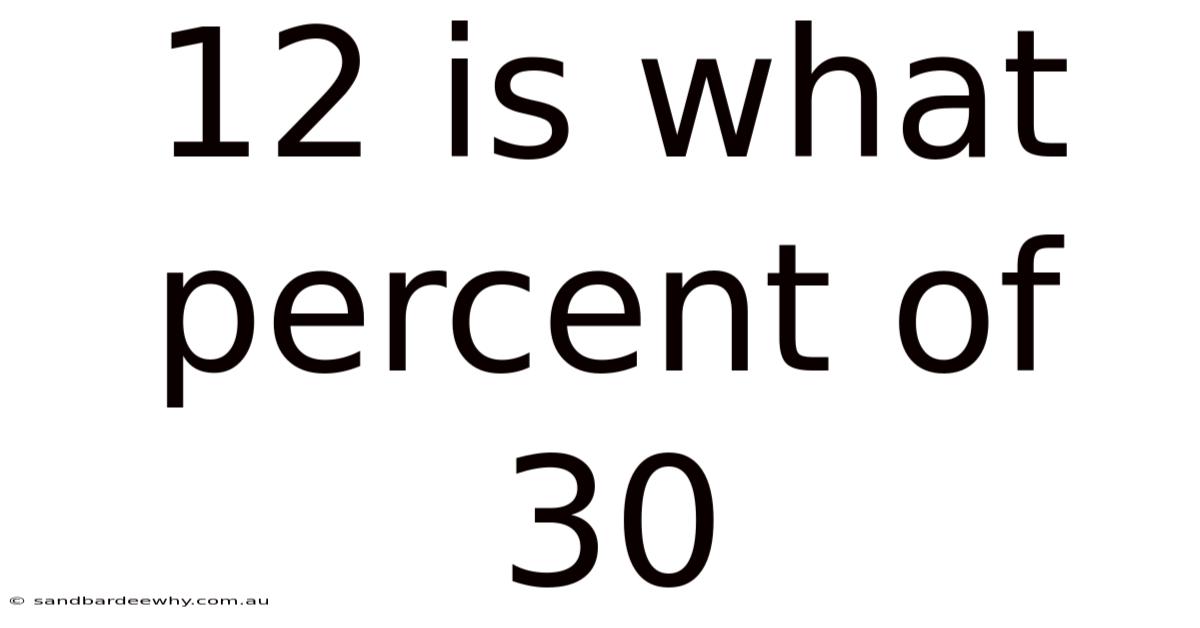
Table of Contents
Imagine you're at a bustling farmers market, eyeing a basket of vibrant, juicy strawberries. The sign says "30 Strawberries for $5," but you only want a handful. You pick out 12 perfect berries and wonder, "What portion of the whole basket am I taking?" This everyday scenario is a perfect example of calculating percentages, a skill that helps us understand proportions and make informed decisions. Knowing "12 is what percent of 30" translates to understanding your share of the strawberry basket.
In the realm of numbers, percentages offer a clear and concise way to express relative quantities. They allow us to compare different values and understand their relationships, whether we're calculating discounts, tracking growth rates, or analyzing statistical data. Understanding percentages is not just a mathematical skill; it's a fundamental tool for navigating the world around us. Let's explore how to precisely determine what percentage 12 represents out of 30, and delve into the broader applications of percentage calculations.
Understanding Percentages: A Comprehensive Guide
Percentages are a fundamental concept in mathematics, used daily in various contexts from finance to statistics. Understanding how to calculate and interpret percentages is essential for making informed decisions and comprehending quantitative data. The question "12 is what percent of 30?" serves as an excellent starting point to explore the broader concept of percentages.
Defining Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "per hundred." Therefore, when we say "x percent," we mean x out of 100. Percentages are denoted by the symbol "%". For instance, 50% means 50 out of 100, which is equivalent to the fraction 1/2 or the decimal 0.5. This standardization allows for easy comparison and understanding of proportions.
The Basic Formula
The basic formula for calculating percentages is:
Percentage = (Part / Whole) * 100
Here:
- Part is the specific quantity you are interested in.
- Whole is the total quantity or the reference value.
To find what percentage 12 is of 30, we use the formula as follows:
Percentage = (12 / 30) * 100
Percentage = 0.4 * 100
Percentage = 40%
Thus, 12 is 40% of 30.
Historical Context
The concept of percentages has ancient roots. In ancient Rome, Emperor Augustus levied a tax known as centesima rerum venalium, which was 1/100 of the goods sold at auction. This can be seen as an early form of percentage calculation. However, the modern concept of percentages, along with the % symbol, became widespread during the 15th century. Merchants and traders used percentages to calculate profits, losses, and interest rates.
The formalization of percentages played a significant role in the development of modern finance and commerce. As trade and banking became more sophisticated, the need for a standardized way to express proportions became essential. The introduction of percentages provided a clear and efficient method for representing these proportions, facilitating communication and calculation in financial transactions.
Practical Applications
Percentages are ubiquitous in everyday life. Here are some common applications:
- Finance: Interest rates, investment returns, inflation rates, and discounts are often expressed as percentages.
- Retail: Sales discounts (e.g., "20% off"), markup percentages, and profit margins are crucial for both businesses and consumers.
- Statistics: Percentages are used to represent data in surveys, polls, and research studies, making it easier to understand and compare different groups.
- Education: Grades are often given as percentages, providing a standardized way to assess student performance.
- Health: Body fat percentage, daily recommended intakes of nutrients, and medication dosages are often expressed as percentages.
Common Misconceptions
Despite their widespread use, percentages can sometimes be confusing. Here are a few common misconceptions:
- Confusing Percentage and Percentage Points: A percentage is a relative measure, while a percentage point is an absolute difference between two percentages. For example, if a company's profit margin increases from 10% to 15%, it has increased by 5 percentage points. The percentage increase, however, is ((15-10)/10) * 100 = 50%.
- Incorrectly Calculating Percentage Change: When calculating the percentage change between two values, it’s crucial to use the correct base. The formula is ((New Value - Old Value) / Old Value) * 100. For example, if a product's price increases from $20 to $25, the percentage increase is ((25-20)/20) * 100 = 25%.
- Misunderstanding Compound Interest: Compound interest involves earning interest on the initial principal and the accumulated interest from previous periods. Failing to understand how compounding works can lead to underestimating the growth of investments over time.
Advanced Concepts
Beyond basic calculations, percentages are used in more complex financial and statistical analyses:
- Weighted Averages: In situations where different data points have different levels of importance, weighted averages are used. Each data point is multiplied by its weight (expressed as a percentage), and the results are summed to obtain the weighted average.
- Index Numbers: Index numbers, such as the Consumer Price Index (CPI), use percentages to track changes in prices or quantities over time. They provide a standardized way to compare values relative to a base period.
- Statistical Analysis: Percentages are used in hypothesis testing, confidence intervals, and regression analysis to interpret and present data.
Trends and Latest Developments
The use of percentages continues to evolve with advancements in technology and data analysis. Here are some current trends and developments:
Data Visualization
In the age of big data, data visualization tools use percentages to create compelling and informative graphics. Software like Tableau, Power BI, and Python libraries (e.g., Matplotlib, Seaborn) enable users to display percentages in charts, graphs, and dashboards. These visualizations make it easier to identify trends, patterns, and outliers in large datasets.
Artificial Intelligence and Machine Learning
AI and machine learning algorithms use percentages to evaluate model performance and make predictions. For example, the accuracy of a classification model might be expressed as a percentage, indicating the proportion of correct predictions out of the total number of predictions. Percentiles are also used in anomaly detection to identify unusual observations in datasets.
Financial Technology (FinTech)
FinTech companies leverage percentages in various applications, including:
- Personal Finance Management: Apps that track spending habits often use percentages to show how income is allocated across different categories (e.g., housing, food, entertainment).
- Investment Platforms: Robo-advisors use algorithms to create investment portfolios based on risk tolerance, which is often expressed as a percentage.
- Cryptocurrency: Percentage changes are used to track the volatility of cryptocurrencies and other digital assets.
E-commerce
In e-commerce, percentages play a vital role in pricing strategies, marketing campaigns, and customer analytics. Retailers use percentages to offer discounts, calculate conversion rates, and analyze customer behavior. A/B testing, which involves comparing two versions of a webpage or app, often uses percentages to determine which version performs better.
Expert Insights
Experts emphasize the importance of data literacy, which includes the ability to understand and interpret percentages accurately. According to financial advisors, understanding interest rates, investment returns, and inflation rates is crucial for making informed financial decisions. Statisticians highlight the importance of using percentages correctly in research studies to avoid misinterpretations and biases.
Tips and Expert Advice
To master the use of percentages, consider these practical tips and expert advice:
Practice Regularly
The more you practice calculating percentages, the more comfortable you will become with the concept. Try solving real-world problems involving percentages, such as calculating discounts at the store or figuring out how much to tip at a restaurant. Use online calculators and tools to check your work and reinforce your understanding.
Understand the Context
Always consider the context when working with percentages. Ask yourself: What is the "whole" that I am referring to? What does the percentage represent in this particular situation? Understanding the context will help you avoid common errors and interpret percentages accurately.
For example, if you are calculating the percentage increase in sales, make sure to use the initial sales figure as the base. If you are analyzing survey data, be aware of the sample size and potential biases.
Use Visual Aids
Visual aids can be helpful for understanding and communicating percentages. Charts, graphs, and diagrams can make it easier to see the relationships between different values. For example, a pie chart can show how a budget is allocated across different categories, with each slice representing a percentage of the total budget.
Double-Check Your Work
Always double-check your calculations to ensure accuracy. Even a small error can lead to significant misinterpretations. Use a calculator or spreadsheet to verify your results. If possible, ask someone else to review your work.
Seek Clarification When Needed
If you are unsure about how to calculate or interpret a percentage, don't hesitate to seek clarification from a teacher, tutor, or online resource. There are many excellent resources available, including textbooks, websites, and video tutorials.
Expert Tip: Use Percentages to Set Goals
Percentages can be a powerful tool for setting and achieving goals. For example, if you want to save money, you can set a goal to save a certain percentage of your income each month. If you want to improve your health, you can set a goal to increase your exercise time by a certain percentage each week.
Real-World Examples
Here are some real-world examples of how percentages are used:
- Calculating Discounts: If an item is on sale for 25% off, you can calculate the discount by multiplying the original price by 0.25. For example, if the original price is $40, the discount is $40 * 0.25 = $10.
- Calculating Tips: To calculate a 15% tip at a restaurant, multiply the bill amount by 0.15. For example, if the bill is $30, the tip is $30 * 0.15 = $4.50.
- Analyzing Investment Returns: If an investment earns a return of 8% per year, you can calculate the annual earnings by multiplying the initial investment by 0.08. For example, if the initial investment is $10,000, the annual earnings are $10,000 * 0.08 = $800.
FAQ
Q: How do I convert a fraction to a percentage? A: To convert a fraction to a percentage, divide the numerator by the denominator, then multiply by 100. For example, to convert 3/4 to a percentage, calculate (3/4) * 100 = 75%.
Q: What is the difference between a percentage increase and a percentage decrease? A: A percentage increase represents the relative increase between two values, while a percentage decrease represents the relative decrease. The formulas are:
Percentage Increase = ((New Value - Old Value) / Old Value) * 100 Percentage Decrease = ((Old Value - New Value) / Old Value) * 100
Q: How do I calculate a percentage of a number? A: To calculate a percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, to find 20% of 50, calculate 50 * 0.20 = 10.
Q: What is the importance of understanding percentages in financial literacy? A: Understanding percentages is crucial for financial literacy because it allows individuals to make informed decisions about budgeting, saving, investing, and borrowing. Percentages are used to express interest rates, investment returns, inflation rates, and loan terms.
Q: Can percentages be greater than 100%? A: Yes, percentages can be greater than 100% in certain situations, such as when calculating percentage increases. For example, if a company's revenue doubles, the percentage increase is 100%. If it triples, the percentage increase is 200%.
Conclusion
Understanding that 12 is 40% of 30 is just the starting point. Percentages are an indispensable tool for navigating daily life, from calculating discounts to understanding financial statements. By grasping the basic formula, avoiding common misconceptions, and practicing regularly, you can confidently use percentages to make informed decisions and solve real-world problems. Whether you're analyzing data, managing finances, or simply trying to understand proportions, a solid understanding of percentages will empower you to make sense of the numbers around you.
Now that you have a comprehensive understanding of percentages, take the next step! Practice applying these concepts to everyday scenarios, explore advanced topics like compound interest and statistical analysis, and share your knowledge with others. Understanding percentages is not just a mathematical skill; it's a key to unlocking a deeper understanding of the world.
Latest Posts
Latest Posts
-
Describe The Main Parts Of A Proof
Nov 23, 2025
-
What Is 4 20 As A Percent
Nov 23, 2025
-
How To Turn Whole Numbers Into Fractions
Nov 23, 2025
-
When Does The Book The Outsiders Take Place
Nov 23, 2025
-
12 Is What Percent Of 30
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about 12 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.