15 Is 25 Of What Number
sandbardeewhy
Nov 26, 2025 · 12 min read
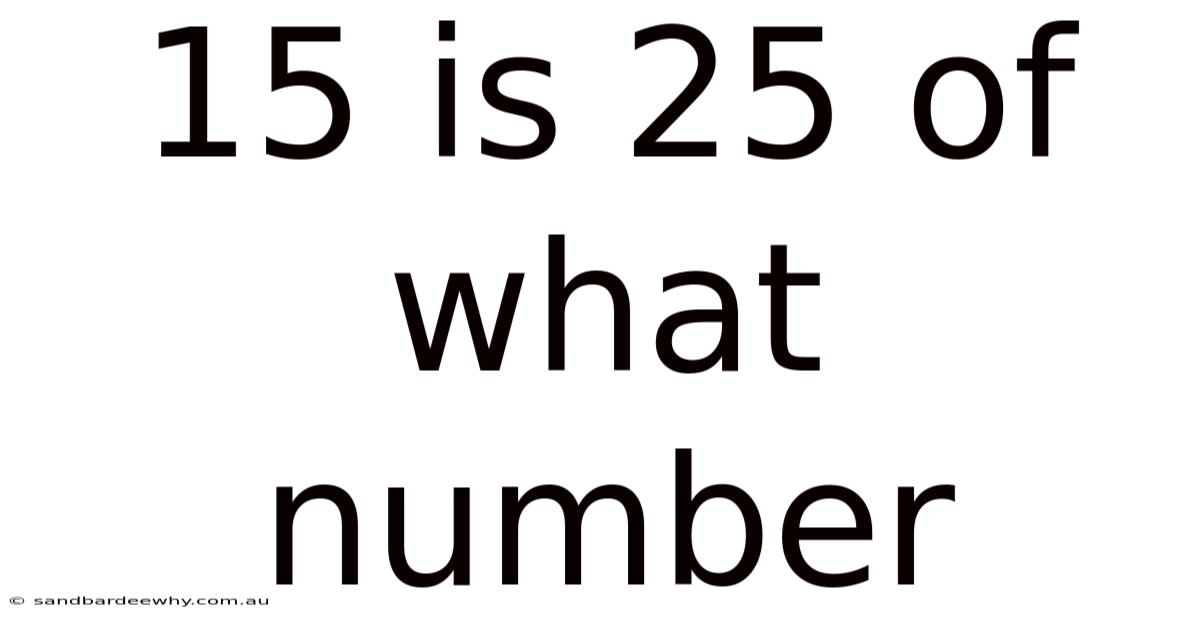
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a vibrant display of organic apples. A sign proclaims, "Today only: 25% off!" You spot a bag containing 15 apples and wonder what the full number of apples would be if the discount weren't applied. Or perhaps you're managing a team, and 15 completed tasks represent 25% of the overall project. Knowing the total number of tasks is critical for planning and resource allocation. These everyday scenarios highlight the importance of understanding percentages and their applications.
At its core, the question "15 is 25% of what number?" is a fundamental mathematical problem with far-reaching implications. It's not just about crunching numbers; it's about understanding proportions, scaling, and how parts relate to the whole. This concept is vital in personal finance, business analytics, scientific research, and countless other fields. Mastering it allows us to make informed decisions, analyze data accurately, and solve problems effectively. Let's delve into the world of percentages and explore the various methods to unravel this intriguing question.
Main Subheading
Understanding the problem "15 is 25% of what number?" requires a solid grasp of percentages. Percentages are ubiquitous in our daily lives, from calculating discounts and interest rates to interpreting statistical data and understanding proportions in recipes. They provide a standardized way to express a fraction of a whole, making comparisons and calculations easier. Essentially, a percentage is a ratio or a fraction expressed as a part of 100.
The percentage concept is based on the idea of dividing a whole into 100 equal parts. When we say "25%," we mean 25 out of every 100 parts. This simple concept forms the foundation for understanding proportional relationships and solving a wide array of mathematical problems. In the context of our question, we are trying to find the "whole" when we know a specific "part" and the percentage that part represents. This involves reversing the percentage calculation to find the original number before the percentage was applied.
Comprehensive Overview
To truly grasp the essence of "15 is 25% of what number?", let's explore the concept of percentages from its basic definition to the various methods used to solve such problems.
The Definition of Percentage
A percentage, derived from the Latin per centum meaning "out of one hundred," is a way of expressing a number as a fraction of 100. It is denoted using the percent sign, "%". For example, 50% signifies 50 out of 100, or simply one-half. Understanding this foundational concept is crucial before diving into more complex calculations. Percentages provide a standardized way to compare different quantities or proportions, making them indispensable in various fields, from finance to statistics.
The Foundation of Percentage Calculations
At its core, a percentage calculation involves relating a part to a whole. The basic formula to calculate a percentage is:
Percentage = (Part / Whole) × 100
In this formula, "Part" is the specific amount we are interested in, and "Whole" is the total amount or the reference value. Multiplying the fraction by 100 converts the ratio into a percentage. This formula can be rearranged to solve for any of the variables, depending on the information available. For instance, if we know the percentage and the whole, we can find the part. Conversely, if we know the part and the percentage, we can find the whole, which is exactly what we aim to do in our problem.
Different Methods to Solve Percentage Problems
There are several ways to solve the problem "15 is 25% of what number?". Each method offers a unique approach, and understanding these different techniques can enhance your problem-solving skills.
-
The Algebraic Method: This is a formal and precise approach using equations. If we let 'x' be the unknown number, we can translate the problem into an equation:
25% of x = 15
Converting the percentage to a decimal, we get:
- 25x = 15
To solve for 'x', we divide both sides of the equation by 0.25:
x = 15 / 0.25
x = 60
Thus, 15 is 25% of 60. The algebraic method is highly reliable and applicable to more complex percentage problems.
-
The Proportion Method: This method involves setting up a proportion to find the unknown number. We can express the relationship as:
25 / 100 = 15 / x
Cross-multiplying gives us:
25x = 1500
Dividing both sides by 25, we find:
x = 60
The proportion method relies on the principle that equivalent ratios are equal. It is particularly useful for visual learners as it provides a clear comparison between the part and the whole.
-
The Unitary Method: This approach focuses on finding the value of 1% first and then scaling up to find the whole (100%).
If 25% is 15, then 1% is 15 / 25 = 0.6
To find 100%, we multiply 0.6 by 100:
100% = 0.6 × 100 = 60
The unitary method is intuitive and helps in understanding the proportional relationship in a step-by-step manner.
-
The Visual Method: For those who prefer a more visual representation, this method can be quite effective. Imagine a pie chart where the whole pie represents 100%. If 25% of the pie is equal to 15, then we can visually divide the pie into four equal parts, each representing 25%. Since one part (25%) is 15, the whole pie (100%) would be 4 times 15, which is 60.
Why These Methods Work
Each of these methods works because they are based on the fundamental principles of proportional reasoning. The algebraic method uses the precision of equations to isolate the unknown variable. The proportion method leverages the equality of ratios, while the unitary method breaks down the problem into smaller, more manageable steps. The visual method provides a tangible representation of the proportional relationship, making it easier to grasp.
Trends and Latest Developments
While the core concept of percentages remains constant, its application and interpretation are continuously evolving with new trends and developments in various fields.
Data Analysis and Statistics
In data analysis and statistics, percentages are used extensively to summarize and interpret large datasets. For example, understanding percentage change is crucial in tracking economic indicators, such as GDP growth or inflation rates. Recent trends emphasize the importance of not only presenting percentage changes but also providing the absolute values to avoid misleading interpretations. This is because a large percentage change from a small base can sometimes appear more significant than it actually is.
Finance and Investment
In finance and investment, percentages are fundamental in calculating returns, interest rates, and portfolio allocations. A growing trend is the use of compounding interest, where interest is earned not only on the principal amount but also on the accumulated interest. Understanding how compounding interest works, often expressed as an annual percentage yield (APY), is critical for making informed investment decisions. Moreover, the use of percentage-based fees, such as management fees charged by investment advisors, is under increased scrutiny, with a focus on transparency and value for investors.
Retail and E-commerce
In the retail and e-commerce sectors, percentages are used to offer discounts, calculate sales tax, and analyze marketing campaign performance. A recent trend is the use of dynamic pricing, where prices are adjusted in real-time based on demand and other factors. These adjustments are often expressed as percentage increases or decreases. Additionally, e-commerce platforms rely heavily on conversion rates, which are calculated as the percentage of visitors who make a purchase. Optimizing conversion rates is a key focus for online retailers, driving innovation in website design, user experience, and marketing strategies.
Public Health and Policy
In public health and policy, percentages are used to track disease prevalence, vaccination rates, and public opinion on various issues. Understanding statistical significance is crucial when interpreting percentage changes in these areas. For example, a small percentage increase in vaccination rates may not be statistically significant if the sample size is small or if there is significant variability in the data. Policymakers need to consider both the percentage change and the absolute numbers to make informed decisions.
Professional Insights
Staying current with these trends requires a multifaceted approach. Professionals should continuously update their knowledge through industry publications, academic research, and professional development courses. Critical thinking is essential to interpret percentage data accurately and avoid common pitfalls, such as overlooking the base value or misinterpreting statistical significance. Furthermore, effective communication is key to conveying percentage-based information clearly and transparently to stakeholders.
Tips and Expert Advice
To master the use of percentages and confidently solve problems like "15 is 25% of what number?", here are some practical tips and expert advice:
Develop a Strong Foundation
Ensure you have a solid understanding of the basic concepts of percentages, ratios, and proportions. This includes knowing how to convert percentages to decimals and fractions, and vice versa. Without a strong foundation, more complex percentage problems can become confusing and difficult to solve.
Start with simple exercises, such as calculating percentages of familiar numbers (e.g., 10% of 100, 50% of 50) and gradually move towards more challenging problems. Practice these fundamentals regularly to reinforce your understanding and build confidence.
Choose the Right Method
As discussed earlier, there are several methods to solve percentage problems, including the algebraic method, the proportion method, and the unitary method. Each method has its strengths and weaknesses, and the best approach often depends on the specific problem and your personal preference.
Experiment with different methods to find the ones that work best for you. For example, if you prefer a more structured and formal approach, the algebraic method may be ideal. If you are a visual learner, the proportion method or the visual method may be more effective.
Estimate and Check Your Answers
Before diving into calculations, take a moment to estimate the answer. This can help you identify potential errors and ensure that your final answer is reasonable. For example, in the problem "15 is 25% of what number?", you can reason that since 25% is one-quarter, the whole number should be approximately four times 15, which is around 60.
After calculating your answer, always check your work to ensure accuracy. You can do this by plugging your answer back into the original problem. For instance, if you find that 15 is 25% of 60, you can verify this by calculating 25% of 60 and confirming that it equals 15.
Use Real-World Examples
One of the best ways to master percentages is to apply them to real-world scenarios. This can help you see the practical relevance of percentages and make the learning process more engaging.
Look for opportunities to use percentages in your daily life, such as calculating discounts while shopping, figuring out tips at restaurants, or tracking your personal finances. By actively using percentages in these contexts, you will develop a deeper understanding and improve your problem-solving skills.
Break Down Complex Problems
Complex percentage problems can often be broken down into smaller, more manageable steps. This can make the problem less intimidating and easier to solve.
For example, if you need to calculate a percentage increase followed by a percentage decrease, you can break this down into two separate calculations. First, calculate the amount of the increase, then add it to the original value. Next, calculate the amount of the decrease based on the new value, and subtract it to find the final value.
Practice Regularly
Like any mathematical skill, mastering percentages requires consistent practice. The more you practice, the more comfortable and confident you will become.
Set aside some time each week to work on percentage problems. You can find practice problems in textbooks, online resources, or even create your own scenarios. The key is to stay consistent and challenge yourself with progressively more difficult problems.
FAQ
Q: What does "percent" mean?
A: "Percent" comes from the Latin per centum, meaning "out of one hundred." It's a way of expressing a number as a fraction of 100.
Q: How do I convert a percentage to a decimal?
A: To convert a percentage to a decimal, divide the percentage by 100. For example, 25% becomes 0.25 (25 / 100 = 0.25).
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.6 becomes 60% (0.6 × 100 = 60).
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically indicates an increase of more than the original amount. For example, if a company's revenue increases by 150%, it means the revenue is now 2.5 times its original value.
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase is the percentage by which a quantity has increased relative to its initial value. It's calculated as ((New Value - Original Value) / Original Value) × 100. Percentage decrease is the percentage by which a quantity has decreased relative to its initial value. It's calculated as ((Original Value - New Value) / Original Value) × 100.
Conclusion
In conclusion, understanding the problem "15 is 25% of what number?" is a gateway to mastering percentages, a crucial skill in numerous aspects of life. We've explored the definition of percentages, various methods to solve such problems, current trends, and expert tips to enhance your understanding. By applying the algebraic method, proportion method, or unitary method, we consistently arrive at the answer: 15 is 25% of 60.
Now that you've deepened your understanding of percentages, it's time to put your knowledge into action. Try solving similar percentage problems, explore real-world applications, and share your insights with others. Engage in discussions, ask questions, and continue to refine your skills. What other percentage-related questions can you explore, and how can you apply this knowledge to make informed decisions in your personal and professional life? Leave a comment below with your thoughts and experiences!
Latest Posts
Latest Posts
-
For The Following Right Triangle Find The Side Length X
Nov 26, 2025
-
What Is The Difference Between A Motor And A Generator
Nov 26, 2025
-
What Is The Opposite Of A Log
Nov 26, 2025
-
Which Of The Following Situations Is Not A Contingent Liability
Nov 26, 2025
-
15 Is 25 Of What Number
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about 15 Is 25 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.