16 Is What Percent Of 80
sandbardeewhy
Nov 26, 2025 · 11 min read
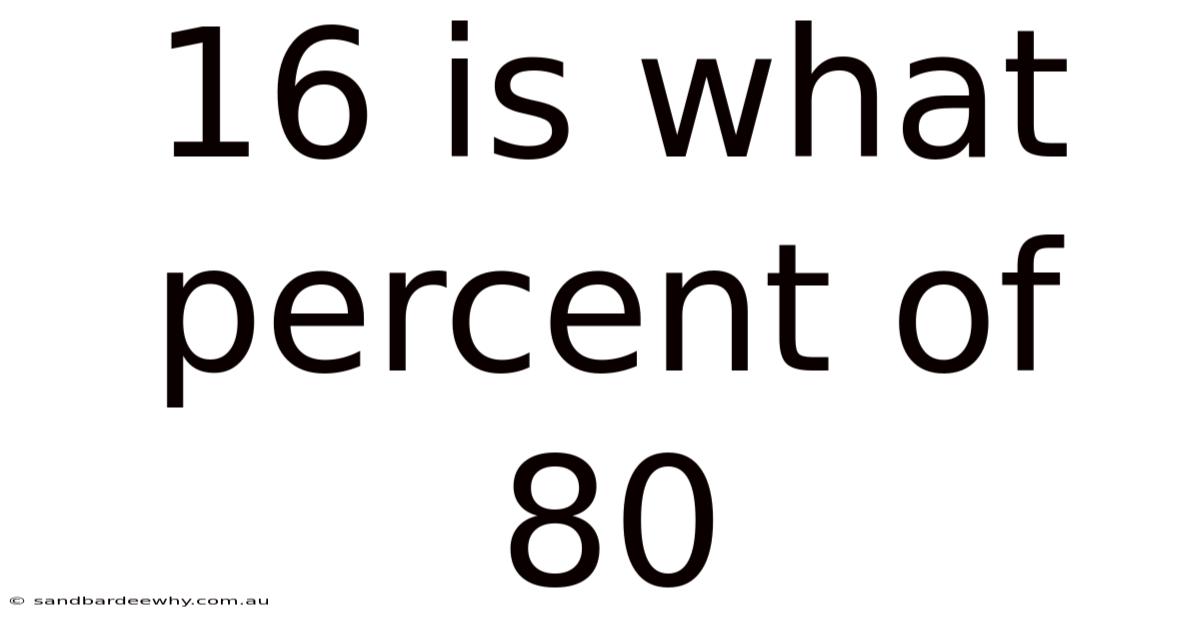
Table of Contents
Imagine you're at a bustling farmers market, eyeing a vibrant display of ripe, juicy apples. The vendor announces a special: "Buy 80 apples, and get 16 free!" Instantly, you wonder, "What percentage discount is that?" Or perhaps you're tracking your fitness progress. You aimed to run 80 miles this month, and you've already logged 16. You're eager to know what percentage of your goal you've achieved. These everyday scenarios highlight the practical relevance of understanding how to calculate percentages.
At its core, the question "16 is what percent of 80?" is a fundamental mathematical problem with wide-ranging applications. Whether you're a student tackling homework, a professional analyzing data, or simply someone trying to make sense of daily deals, mastering percentage calculations is essential. This article will provide a comprehensive guide to understanding and solving this type of problem, equipping you with the knowledge and skills to confidently tackle percentage-related challenges in any context. We'll explore the underlying concepts, delve into practical applications, and offer expert tips to ensure you grasp the material thoroughly.
Main Subheading: Understanding the Basics of Percentage Calculation
Before diving into the specific problem, let's establish a solid foundation in the basics of percentage calculations. Percentages are a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." This simple concept underpins a wide array of mathematical and practical applications, from calculating discounts and taxes to analyzing statistical data and understanding financial reports.
To effectively work with percentages, it's crucial to understand the three key components involved: the base, the part, and the percentage. The base is the total or whole amount, the part is a portion of that whole, and the percentage is the ratio of the part to the base, expressed as a value out of 100. In the question "16 is what percent of 80?", 80 is the base (the whole), 16 is the part (the portion), and we are trying to find the percentage.
The fundamental formula for calculating percentages is:
Percentage = (Part / Base) * 100
This formula provides a direct and reliable method for determining the percentage when you know the part and the base. Let's apply this formula to our initial question and then explore the broader concepts in more detail. In our case, the "part" is 16, and the "base" is 80. Plugging these values into the formula, we get:
Percentage = (16 / 80) * 100
Now, let's break down the calculation:
- Divide 16 by 80: 16 ÷ 80 = 0.2
- Multiply the result by 100: 0.2 * 100 = 20
Therefore, 16 is 20% of 80. This straightforward calculation demonstrates the power and simplicity of the percentage formula.
Comprehensive Overview: Diving Deeper into Percentage Concepts
Now that we've solved the initial problem, let's broaden our understanding by exploring the essential concepts underlying percentage calculations. Percentages are not just abstract numbers; they are powerful tools for comparison, analysis, and decision-making in various fields. Understanding the nuances of percentage calculations allows us to interpret data more effectively and make informed judgments.
The Relationship Between Fractions, Decimals, and Percentages
Percentages are closely related to fractions and decimals. As we saw in the initial calculation, the first step in finding a percentage often involves converting a fraction (part/base) into a decimal. Understanding this relationship is crucial for manipulating and interpreting percentages effectively.
- Fraction to Percentage: To convert a fraction to a percentage, you divide the numerator (top number) by the denominator (bottom number) and then multiply by 100. For example, the fraction 1/4 is equivalent to 0.25 as a decimal, and 25% as a percentage.
- Decimal to Percentage: To convert a decimal to a percentage, you simply multiply the decimal by 100. For example, the decimal 0.75 is equivalent to 75%.
- Percentage to Fraction: To convert a percentage to a fraction, you divide the percentage by 100 and simplify the resulting fraction. For example, 60% is equal to 60/100, which simplifies to 3/5.
- Percentage to Decimal: To convert a percentage to a decimal, you divide the percentage by 100. For example, 90% is equal to 0.9.
Being able to fluidly convert between these forms allows for flexible problem-solving.
Calculating Percentage Increase and Decrease
Percentages are commonly used to express changes in values over time. Understanding how to calculate percentage increase and decrease is essential in various fields, including finance, economics, and statistics. The formulas for calculating percentage increase and decrease are:
- Percentage Increase = [(New Value - Original Value) / Original Value] * 100
- Percentage Decrease = [(Original Value - New Value) / Original Value] * 100
For example, if a product's price increases from $50 to $60, the percentage increase is:
Percentage Increase = [(60 - 50) / 50] * 100 = (10 / 50) * 100 = 20%
Similarly, if a company's revenue decreases from $100,000 to $80,000, the percentage decrease is:
Percentage Decrease = [(100,000 - 80,000) / 100,000] * 100 = (20,000 / 100,000) * 100 = 20%
These calculations are invaluable for tracking trends, assessing performance, and making informed decisions.
Applying Percentages in Real-World Scenarios
Percentages permeate our daily lives, appearing in various contexts, from retail discounts to financial investments. Let's consider a few practical examples:
- Retail Discounts: When a store advertises a "30% off" sale, you can calculate the discount amount by multiplying the original price by 30% (or 0.30). For example, if an item originally costs $100, the discount is $100 * 0.30 = $30, making the sale price $70.
- Taxes: Sales tax is often expressed as a percentage of the purchase price. If the sales tax rate is 7%, you can calculate the tax amount by multiplying the purchase price by 7% (or 0.07). For example, if you buy something for $50, the sales tax is $50 * 0.07 = $3.50, bringing the total cost to $53.50.
- Financial Investments: Investment returns are typically expressed as percentages. If an investment yields a 10% return, it means that for every $100 invested, you earn $10 in profit.
- Statistics: Percentages are frequently used in statistical analysis to represent proportions and distributions. For example, a survey might reveal that 60% of respondents prefer a particular product, providing valuable insights for marketing and product development.
Understanding how percentages are used in these scenarios empowers you to make informed financial decisions, evaluate deals effectively, and interpret statistical data accurately.
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations are generally straightforward, several common mistakes can lead to inaccurate results. Being aware of these pitfalls can help you avoid errors and ensure the accuracy of your calculations.
- Confusing the Base: One of the most common mistakes is misidentifying the base (the whole). Always ensure you are using the correct value as the base when calculating percentages. For example, when calculating a percentage increase, the original value should be used as the base.
- Incorrectly Converting to Decimals: Errors can occur when converting percentages to decimals or vice versa. Remember to divide the percentage by 100 to convert it to a decimal and multiply the decimal by 100 to convert it to a percentage.
- Applying Percentages Sequentially Incorrectly: When applying multiple percentages sequentially, such as a discount followed by a tax, it's crucial to apply them in the correct order. Applying them in the wrong order can lead to incorrect results.
- Rounding Errors: Rounding errors can accumulate and lead to significant inaccuracies, especially in complex calculations. It's best to avoid rounding intermediate results and only round the final answer.
By being mindful of these common mistakes, you can significantly improve the accuracy of your percentage calculations.
The Importance of Estimation and Reasonableness
In practical situations, it's often helpful to estimate percentages before performing precise calculations. Estimation can provide a quick check of your results and help you identify potential errors. Furthermore, considering the reasonableness of your answer can prevent you from accepting nonsensical results.
For example, if you are calculating the percentage that 16 is of 80, you might quickly recognize that 16 is about one-fifth of 80. Since one-fifth is equivalent to 20%, you can estimate that the answer should be around 20%. This quick estimate can help you verify that your calculation is in the right ballpark.
Similarly, if you calculate that 16 is 200% of 80, you should immediately recognize that this answer is unreasonable because 16 is smaller than 80. Cultivating a habit of estimation and reasonableness can significantly enhance your problem-solving skills and prevent costly errors.
Trends and Latest Developments in Percentage Use
In today's data-driven world, the use of percentages continues to evolve and adapt to new challenges and opportunities. Here are some current trends and developments:
- Data Visualization: Percentages are increasingly used in data visualization to present complex information in an accessible and understandable format. Charts, graphs, and infographics often rely on percentages to communicate proportions and trends effectively.
- Machine Learning and AI: Machine learning algorithms and artificial intelligence systems utilize percentages extensively for tasks such as classification, prediction, and performance evaluation. Percentages are used to represent probabilities, confidence levels, and error rates.
- E-commerce and Digital Marketing: E-commerce platforms and digital marketing campaigns heavily rely on percentages to track key metrics such as conversion rates, click-through rates, and return on investment. These percentages provide valuable insights for optimizing marketing strategies and improving business performance.
- Healthcare Analytics: In healthcare, percentages are used to analyze patient outcomes, track disease prevalence, and assess the effectiveness of treatments. For example, percentages can be used to represent the proportion of patients who respond positively to a particular medication.
- Financial Modeling: Financial models frequently employ percentages to project future performance, analyze investment scenarios, and assess risk. Percentages are used to represent growth rates, interest rates, and profit margins.
These trends highlight the enduring relevance of percentages in a wide range of fields and underscore the importance of developing strong percentage calculation skills.
Tips and Expert Advice for Mastering Percentage Calculations
To further enhance your proficiency in percentage calculations, here are some practical tips and expert advice:
- Practice Regularly: The key to mastering any mathematical skill is consistent practice. Work through a variety of percentage problems to reinforce your understanding and build confidence.
- Use Real-World Examples: Relate percentage calculations to real-world scenarios to make the concepts more meaningful and memorable. Think about how percentages are used in everyday situations, such as shopping, cooking, and budgeting.
- Break Down Complex Problems: When faced with complex percentage problems, break them down into smaller, more manageable steps. This approach can help you avoid confusion and ensure accuracy.
- Double-Check Your Work: Always double-check your calculations to catch any errors. Pay close attention to the base, the part, and the placement of the decimal point.
- Utilize Technology: Take advantage of calculators, spreadsheets, and online tools to simplify percentage calculations and verify your results. However, be sure to understand the underlying concepts and not rely solely on technology.
- Seek Clarification: If you encounter difficulties with percentage calculations, don't hesitate to seek clarification from teachers, tutors, or online resources. A clear understanding of the fundamental concepts is essential for success.
By following these tips and seeking expert advice, you can significantly improve your percentage calculation skills and confidently tackle a wide range of problems.
FAQ: Frequently Asked Questions About Percentage Calculations
Q: What is the formula for calculating percentages?
A: The basic formula is: Percentage = (Part / Base) * 100.
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator, then multiply by 100.
Q: How do I convert a percentage to a decimal?
A: Divide the percentage by 100.
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase calculates the relative increase from an original value to a new value, while percentage decrease calculates the relative decrease.
Q: How do I calculate a discount using percentages?
A: Multiply the original price by the discount percentage (expressed as a decimal) to find the discount amount, then subtract the discount amount from the original price.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an original value that has increased significantly.
Q: What does it mean if something is 0%?
A: If something is 0%, it means there is none of it. It represents the absence of that particular quantity.
Q: Why are percentages useful?
A: Percentages are useful because they provide a standardized way to compare proportions and changes across different contexts. They simplify complex data and make it easier to understand.
Conclusion: Mastering Percentages for Everyday Success
In conclusion, understanding how to calculate "16 is what percent of 80" is more than just a mathematical exercise; it's a practical skill that empowers you to navigate everyday situations with confidence. We've explored the fundamental concepts of percentage calculations, delved into real-world applications, and provided expert tips to enhance your proficiency. Remember the core formula: Percentage = (Part / Base) * 100. Mastering this simple formula opens the door to a world of analytical possibilities.
Now that you have a solid understanding of percentages, put your knowledge to the test. Try solving percentage problems in your daily life, whether it's calculating discounts while shopping or tracking your progress towards a fitness goal. Share your insights and challenges in the comments below, and let's continue learning together. What are some creative ways you've used percentages in your life recently?
Latest Posts
Latest Posts
-
What Is Resolution In The Story
Nov 26, 2025
-
A Piece Of String Short Story
Nov 26, 2025
-
16 Is What Percent Of 80
Nov 26, 2025
-
How Were The Maya Organized Politically
Nov 26, 2025
-
Definition Of Plunder In The Bible
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about 16 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.