17 Out Of 25 As A Percentage
sandbardeewhy
Nov 24, 2025 · 11 min read
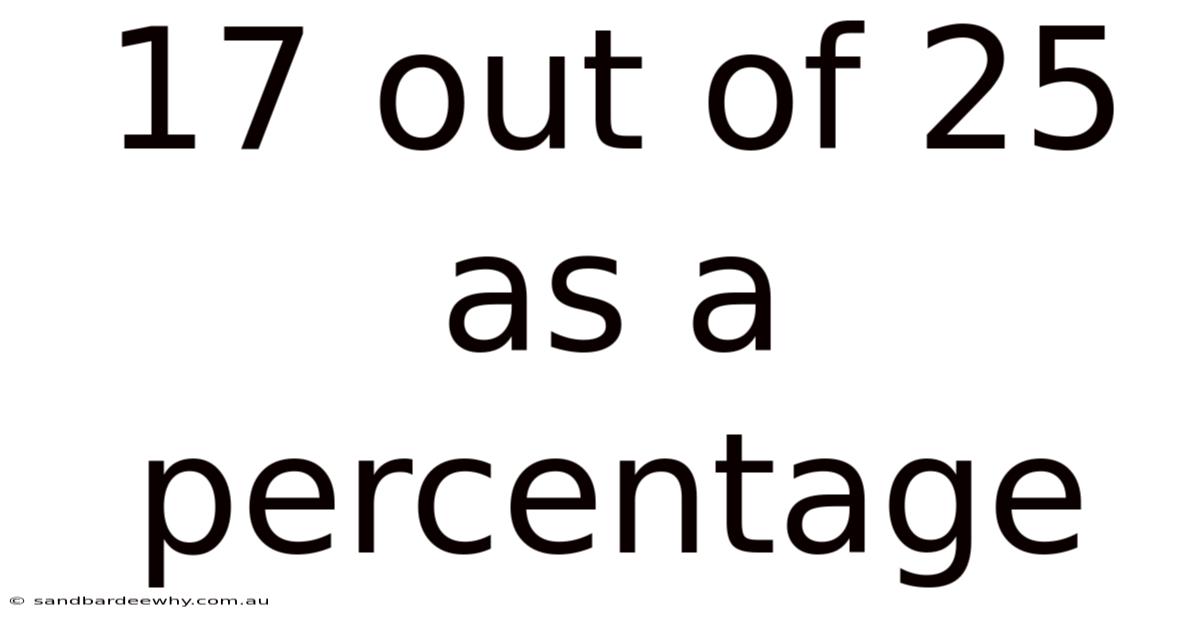
Table of Contents
Imagine you're at a carnival, playing a classic ring toss game. You get 25 rings, aim carefully, and manage to land 17 of them around the bottles. A wave of excitement washes over you, but then comes the curiosity: what percentage of your throws were successful? How well did you actually do?
Or perhaps you're a student facing a pop quiz. There are 25 questions, and after carefully considering each one, you confidently answer 17 correctly. The anticipation builds as you await your score. Knowing the raw number of correct answers is helpful, but understanding it as a percentage gives you a clearer picture of your performance and how it compares to expectations. This conversion from a fraction to a percentage is a fundamental skill with applications far beyond games and quizzes.
Calculating Percentages: Understanding 17 out of 25
Calculating percentages is a foundational skill in mathematics with far-reaching applications in daily life, academics, and professional fields. Understanding how to express one number as a percentage of another allows us to interpret data, compare values, and make informed decisions. When we say "17 out of 25 as a percentage," we're essentially asking what proportion of 25 is represented by 17, expressed in terms of 100.
At its core, a percentage is a way of expressing a fraction or ratio as a part of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, calculating a percentage involves finding an equivalent fraction with a denominator of 100. This standardized representation enables us to easily compare different fractions and proportions. The concept is crucial not only for simple calculations like figuring out discounts or tips but also for more complex analyses in statistics, finance, and science.
The Mathematical Foundation of Percentages
To convert a fraction (like 17/25) into a percentage, we follow a simple formula:
Percentage = (Part / Whole) * 100
Here, "Part" is the number you want to express as a percentage of the "Whole." In our example, 17 is the "Part" and 25 is the "Whole." The formula essentially scales the fraction to a base of 100, making it easier to understand and compare.
Step-by-Step Calculation: 17 out of 25 as a Percentage
Let's apply the formula to calculate 17 out of 25 as a percentage:
-
Identify the "Part" and the "Whole":
- Part = 17
- Whole = 25
-
Divide the "Part" by the "Whole":
- 17 / 25 = 0.68
-
Multiply the result by 100:
-
- 68 * 100 = 68
-
Therefore, 17 out of 25 as a percentage is 68%. This means that 17 represents 68% of 25.
Historical Context of Percentages
The concept of percentages can be traced back to ancient Rome. As early as the Roman Empire, calculations involving hundredths were used for various purposes, including taxation and trade. The Romans, however, did not use the percent sign (%) that we use today. Instead, they would often express fractions as parts of one hundred (per centum).
During the Middle Ages, as trade and commerce flourished, the use of percentages became more widespread. Italian merchants frequently used percentages in calculating profits, interest, and taxes. The percent sign (%) gradually evolved from various abbreviations used in manuscripts to represent "per cento." By the 17th century, the symbol had taken on a form similar to what we recognize today. The standardization of percentages has greatly facilitated mathematical and financial operations across different cultures and languages.
The Ubiquitous Use of Percentages in Modern Life
Percentages are pervasive in modern life, appearing in numerous contexts across diverse fields. In finance, interest rates, investment returns, and inflation rates are all commonly expressed as percentages. Understanding these percentages is crucial for making informed financial decisions, whether it's choosing a savings account, evaluating an investment opportunity, or budgeting for expenses.
In retail, discounts and sales are often advertised as percentages, enabling consumers to quickly assess the savings they can achieve. "20% off" or "50% off" are familiar phrases that help shoppers gauge the value of a purchase. In education, test scores and grades are frequently expressed as percentages, providing a standardized measure of student performance. This allows educators to compare student achievement across different assignments and assessments.
In healthcare, percentages are used to communicate the effectiveness of treatments, the prevalence of diseases, and the risk factors associated with certain conditions. For example, a doctor might inform a patient that a particular medication has a 90% success rate. In sports, percentages are used to track performance metrics such as shooting accuracy, save percentages, and win rates, providing valuable insights for players, coaches, and fans alike. The widespread use of percentages underscores their importance as a versatile and practical tool for communication, analysis, and decision-making.
Understanding Percentage Increase and Decrease
While calculating a simple percentage is straightforward, it's equally important to understand how to calculate percentage increase and decrease. These calculations are used to determine the relative change in a quantity over time. The formulas are as follows:
- Percentage Increase = [(New Value - Old Value) / Old Value] * 100
- Percentage Decrease = [(Old Value - New Value) / Old Value] * 100
For example, if a product's price increases from $20 to $25, the percentage increase is:
Percentage Increase = [(25 - 20) / 20] * 100 = (5 / 20) * 100 = 25%
Conversely, if the price decreases from $25 to $20, the percentage decrease is:
Percentage Decrease = [(25 - 20) / 25] * 100 = (5 / 25) * 100 = 20%
These calculations are essential for analyzing trends, evaluating performance, and making informed decisions in various fields.
Trends and Latest Developments in Percentage Use
In recent years, the use of percentages has remained stable, but the way they are presented and interpreted has evolved. Data visualization tools and techniques are increasingly used to present percentages in a clear and engaging manner. Charts, graphs, and infographics help to communicate proportional relationships more effectively than raw numbers alone.
One notable trend is the increased emphasis on understanding the context behind percentages. While a percentage can provide a snapshot of a particular situation, it's crucial to consider the underlying data and factors that may influence the result. For instance, a high percentage success rate for a medical treatment may not be meaningful if the sample size is small or if the study is not well-controlled.
Another trend is the growing awareness of the potential for percentages to be misleading or misinterpreted. Selective reporting of percentages, biased sampling, and lack of transparency can all distort the true picture. Therefore, critical thinking and statistical literacy are essential skills for interpreting percentages accurately and avoiding common pitfalls.
From a professional standpoint, expertise in understanding and applying percentages remains highly valued across various industries. Financial analysts, marketers, scientists, and educators all rely on percentages to analyze data, communicate findings, and make informed decisions. Professional insights often involve not just calculating percentages but also interpreting their significance in the context of specific business objectives or research questions. This includes understanding the limitations of percentages, potential sources of error, and the need for further investigation to draw meaningful conclusions.
Tips and Expert Advice for Working with Percentages
Working with percentages can be straightforward, but it's essential to understand some key principles and best practices to ensure accuracy and avoid common mistakes. Here are some practical tips and expert advice for handling percentages effectively:
-
Understand the Base:
- Always clarify what the percentage is based on. For example, a 10% increase on a small number will be very different from a 10% increase on a large number. Knowing the base provides context and helps you interpret the percentage accurately.
- Consider a scenario where a company reports a 50% increase in sales. At first glance, this might seem impressive. However, if the company's initial sales were very low, the actual increase in revenue might be modest. Conversely, a smaller percentage increase from a larger base could represent a more substantial gain.
-
Convert Percentages to Decimals:
- When performing calculations involving percentages, it's often easier to convert them to decimals first. To convert a percentage to a decimal, divide it by 100. For example, 25% becomes 0.25, and 75% becomes 0.75.
- Using decimals simplifies calculations and reduces the risk of errors. For instance, if you want to calculate 20% of $150, converting 20% to 0.20 and multiplying it by $150 gives you $30, which is the correct answer.
-
Avoid Percentage of Percentage Errors:
- Be cautious when dealing with percentages of percentages. For example, if a product's price is reduced by 20% and then further reduced by 10%, the total reduction is not 30%. The second percentage is applied to the already reduced price, resulting in a smaller overall discount.
- To calculate the total reduction accurately, you need to apply each percentage sequentially. If the original price is $100, a 20% reduction brings it down to $80. A 10% reduction on $80 is $8, making the final price $72. The total reduction is $28, which is 28% of the original price, not 30%.
-
Use Percentages for Comparison:
- Percentages are excellent for comparing different sets of data, especially when the sizes of the sets vary. Comparing raw numbers might be misleading, but percentages provide a standardized way to assess relative proportions.
- For example, if two schools have different numbers of students, comparing the number of students who passed an exam might not be meaningful. However, comparing the percentage of students who passed provides a more accurate assessment of each school's performance.
-
Estimate and Check:
- Before performing precise calculations, estimate the answer to ensure that your final result is reasonable. This can help you catch errors and avoid mistakes.
- For example, if you're calculating a 15% tip on a $60 bill, estimate that 10% of $60 is $6, so 15% should be around $9. This quick check can help you verify that your calculated tip is in the right ballpark.
-
Be Mindful of Rounding:
- When rounding percentages, be consistent and use appropriate rounding rules. Rounding errors can accumulate and lead to significant discrepancies, especially when dealing with large numbers or complex calculations.
- For example, if you're calculating the percentage of multiple categories, ensure that the rounded percentages add up to 100%. If they don't, adjust the rounding to maintain accuracy.
-
Context Matters:
- Always consider the context in which the percentage is presented. A percentage without context can be misleading or meaningless. Understand the underlying data, the source of the information, and any potential biases or limitations.
- For example, a high percentage satisfaction rate might be less impressive if the survey was conducted among a small, select group of customers who are already highly engaged with the product or service.
By following these tips and expert advice, you can enhance your understanding of percentages and use them more effectively in various situations.
Frequently Asked Questions (FAQ)
-
Q: How do I convert a decimal to a percentage?
- A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 becomes 75%.
-
Q: How do I find the original value if I know the percentage and the resulting value?
- A: Divide the resulting value by the percentage (expressed as a decimal). For example, if 20% of a number is 50, the original number is 50 / 0.20 = 250.
-
Q: What is the difference between percentage and percentage points?
- A: A percentage is a proportion out of 100, while percentage points represent the arithmetic difference between two percentages. For example, if a rate increases from 10% to 12%, it has increased by 2 percentage points.
-
Q: How do I calculate the percentage change between two values?
- A: Use the formula: [(New Value - Old Value) / Old Value] * 100. This will give you the percentage increase or decrease.
-
Q: Can a percentage be greater than 100%?
- A: Yes, a percentage can be greater than 100% if the "Part" is greater than the "Whole." For example, if a company's revenue doubles, it has increased by 100%. If it triples, it has increased by 200%.
Conclusion
Understanding how to calculate and interpret percentages is a fundamental skill with widespread applications. Whether you're calculating 17 out of 25 as a percentage or analyzing complex financial data, the ability to work with percentages effectively is essential for making informed decisions. Remember to always consider the context, understand the base, and avoid common pitfalls.
Now that you have a comprehensive understanding of percentages, put your knowledge to the test! Calculate percentages in your daily life, analyze data, and make informed decisions. Share your insights with others and help them understand the power of percentages. Engage in discussions and contribute to a more statistically literate society.
Latest Posts
Latest Posts
-
Where Is Zambia Located In Africa
Nov 24, 2025
-
How Much Is 3 Quarts In A Cup
Nov 24, 2025
-
17 Out Of 25 As A Percentage
Nov 24, 2025
-
Summary Of Chapter 12 Lord Of The Flies
Nov 24, 2025
-
How To Find Out Average Speed
Nov 24, 2025
Related Post
Thank you for visiting our website which covers about 17 Out Of 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.