19 Is What Percent Of 25
sandbardeewhy
Nov 22, 2025 · 10 min read
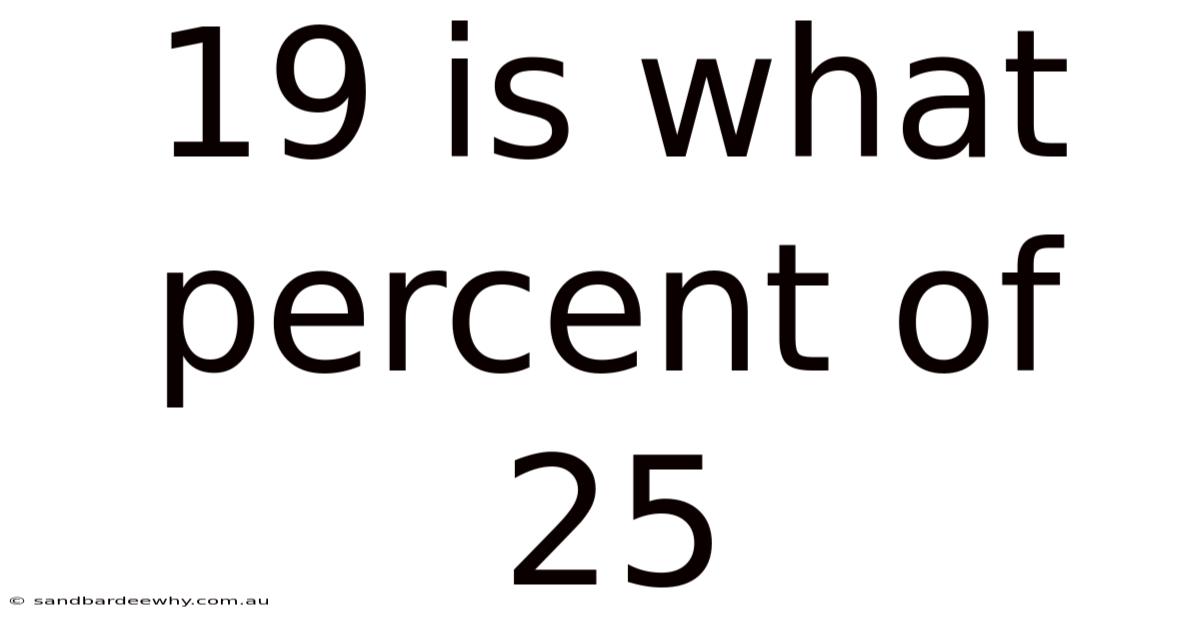
Table of Contents
Imagine you're at a bustling farmers market, eyeing a basket of vibrant red apples. A sign proclaims "25 Apples - Special Price!" You only want 19, and you're trying to figure out what fraction of the basket that represents to negotiate a fair price. This simple scenario highlights a common mathematical question: 19 is what percent of 25?
Understanding percentages is a fundamental skill, applicable in countless everyday situations – from calculating discounts while shopping to understanding statistics in the news. It's not just about crunching numbers; it's about developing a powerful tool for interpreting and navigating the world around us. Let's delve into how to solve this specific problem and explore the broader concepts of percentages.
Decoding the Percentage Puzzle: 19 is What Percent of 25?
At its core, finding what percentage one number is of another involves expressing a part of a whole as a fraction out of 100. In our case, 19 is the "part," and 25 is the "whole." To determine the percentage, we need to follow a straightforward process that transforms this relationship into a percentage value.
The foundation of percentage calculations lies in understanding proportions. A percentage is simply a way of expressing a ratio or fraction with a denominator of 100. This allows us to easily compare different proportions and understand their relative sizes. The word "percent" itself comes from the Latin per centum, meaning "out of one hundred." This etymology provides a direct clue to the mathematical operation involved.
The formula for calculating the percentage is quite simple: (Part / Whole) * 100. Applying this to our problem, we have (19 / 25) * 100. The first step is to divide 19 by 25, which results in 0.76. Then, we multiply 0.76 by 100, which gives us 76. Therefore, 19 is 76% of 25.
This calculation can be visualized in several ways. Imagine a pie chart divided into 25 equal slices. Nineteen of those slices would represent 76% of the entire pie. Alternatively, consider a bar graph where the full bar represents 25 units. The portion of the bar corresponding to 19 units would visually demonstrate the 76% relationship. Understanding this core principle opens the door to a wider range of percentage-related calculations.
A Comprehensive Look at Percentages
To truly grasp the significance of our "19 is what percent of 25" problem, it's helpful to explore the broader world of percentages. Percentages are ubiquitous in modern life, used to express everything from interest rates to survey results. Understanding their underlying principles allows for informed decision-making and critical analysis.
The concept of percentages has ancient roots. While the modern percentage symbol (%) is relatively recent, the idea of expressing fractions in relation to a standard base dates back to ancient civilizations. Romans, for example, often calculated taxes as fractions of assets, frequently using a base of 100. During the Middle Ages, as trade and commerce flourished, the need for standardized methods of calculating interest, profit margins, and taxes became increasingly important. This led to the widespread adoption of percentages as a convenient and universally understood tool.
Percentages are closely related to decimals and fractions. As we saw in our initial calculation, converting a fraction to a percentage involves dividing the numerator by the denominator and then multiplying by 100. This highlights the equivalence between fractions, decimals, and percentages. For instance, the fraction 1/4 is equivalent to the decimal 0.25 and the percentage 25%. This interconvertibility is essential for solving various mathematical problems and understanding different representations of the same value.
Beyond simple calculations, percentages are used in various statistical analyses. They help us understand proportions within datasets, compare different groups, and identify trends. For example, market researchers use percentages to analyze consumer preferences, while scientists use them to express the accuracy of experimental results. The power of percentages lies in their ability to normalize data, allowing for meaningful comparisons regardless of the absolute size of the underlying numbers.
Understanding how to calculate percentage increase and decrease is also crucial. Percentage increase measures the relative change in a value over time, expressed as a percentage of the original value. The formula for percentage increase is: [(New Value - Original Value) / Original Value] * 100. Conversely, percentage decrease measures the relative reduction in a value over time, calculated using a similar formula: [(Original Value - New Value) / Original Value] * 100. These calculations are widely used in finance, economics, and various other fields to track changes and evaluate performance.
Current Trends and Developments in Percentage Usage
The digital age has amplified the importance of understanding and interpreting percentages. With the proliferation of data and the increasing reliance on data-driven decision-making, the ability to critically analyze percentage-based information is more crucial than ever. This section will explore current trends and developments in how percentages are used and perceived.
One notable trend is the increasing use of percentages in data visualization. Charts, graphs, and infographics often rely on percentages to present complex information in an easily digestible format. However, this also presents challenges. Misleading visualizations can distort the true picture, leading to misinterpretations and flawed conclusions. It's essential to critically evaluate how percentages are presented in visual formats, paying attention to the scale, context, and potential biases.
Another development is the growing awareness of the psychological impact of percentages. Studies have shown that the way percentages are framed can significantly influence people's perceptions and decisions. For example, a product advertised as "20% off" may seem more attractive than the same product described as "80% of the original price," even though the actual discount is the same. Marketers often exploit this psychological effect to boost sales. Understanding these cognitive biases is crucial for making informed choices as consumers.
The use of percentages in financial literacy is also gaining prominence. Financial institutions and educational organizations are increasingly emphasizing the importance of understanding interest rates, investment returns, and loan terms, all of which are typically expressed as percentages. Empowering individuals with financial literacy skills helps them make sound financial decisions, manage their budgets effectively, and avoid predatory lending practices.
Furthermore, percentages play a vital role in understanding and addressing social and economic inequalities. Data on income distribution, poverty rates, and educational attainment are often presented as percentages, allowing policymakers to identify disparities and develop targeted interventions. However, it's essential to interpret these statistics with caution, considering the limitations of the data and the potential for unintended consequences.
In the realm of artificial intelligence (AI) and machine learning, percentages are used extensively to evaluate the performance of algorithms. Metrics such as accuracy, precision, and recall are often expressed as percentages, providing a standardized way to compare different models. As AI becomes increasingly integrated into various aspects of our lives, understanding these performance metrics is essential for ensuring that AI systems are reliable, fair, and effective.
Practical Tips and Expert Advice for Mastering Percentages
While the basic formula for calculating percentages is straightforward, applying it effectively in real-world scenarios requires practice and a nuanced understanding of the underlying concepts. Here are some practical tips and expert advice to help you master percentages:
-
Practice Regularly: The more you work with percentages, the more comfortable you'll become with the calculations and the different ways they can be applied. Try solving percentage-related problems in your daily life, such as calculating discounts at the store or figuring out tips at a restaurant. Numerous online resources and practice worksheets can also help you hone your skills.
-
Understand the Context: Percentages are always relative to a specific context. Before performing any calculations, take the time to understand what the "whole" represents and how the "part" relates to it. This will help you avoid common mistakes and ensure that your calculations are meaningful. For example, when calculating a percentage increase, make sure you're using the correct original value as the base.
-
Convert to Decimals: When performing complex calculations involving percentages, it can be helpful to convert them to decimals first. This simplifies the arithmetic and reduces the risk of errors. To convert a percentage to a decimal, simply divide it by 100. For example, 75% becomes 0.75. Remember to convert the decimal back to a percentage at the end of the calculation if necessary.
-
Use Estimation: Before performing any calculations, try to estimate the answer mentally. This will help you check your work and identify any obvious errors. For example, if you're trying to calculate 20% of 150, you know the answer should be around 30 (since 10% of 150 is 15, and 20% is double that). If your calculated answer is significantly different from your estimate, double-check your work.
-
Beware of Misleading Percentages: Be wary of percentages that are presented without adequate context or that seem too good to be true. Always ask yourself what the percentage is based on and whether the comparison is fair. For example, a company might advertise a "500% increase in sales!" but fail to mention that the increase is from a very low base, making the actual sales figures less impressive.
-
Utilize Technology: Take advantage of calculators, spreadsheets, and online tools to simplify percentage calculations. These tools can save you time and reduce the risk of errors, especially when dealing with complex calculations. However, it's still important to understand the underlying principles so you can interpret the results correctly.
-
Learn About Compound Interest: Compound interest is a powerful concept that can significantly impact your financial well-being. Understanding how it works is essential for making informed investment decisions. Compound interest is calculated on the initial principal and the accumulated interest from previous periods. This means that your money grows exponentially over time.
-
Apply Percentages to Real-World Situations: Look for opportunities to apply your knowledge of percentages to real-world situations. This will help you reinforce your understanding and appreciate the practical value of this skill. For example, you can use percentages to compare prices at different stores, calculate your savings rate, or track your progress towards your financial goals.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage increase?
A: The formula for percentage increase is: [(New Value - Original Value) / Original Value] * 100. For example, if a price increases from $20 to $25, the percentage increase is [($25 - $20) / $20] * 100 = 25%.
Q: What is the difference between a percentage and a percentage point?
A: A percentage is a ratio expressed as a fraction of 100, while a percentage point is a simple difference between two percentages. For example, if an interest rate increases from 5% to 7%, that's a 2 percentage point increase.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100. For example, to convert 3/4 to a percentage, calculate (3 / 4) * 100 = 75%.
Q: How do I find the original value if I know the percentage and the final value?
A: If you know the final value after a percentage increase or decrease, you can use the following formula to find the original value: Original Value = Final Value / (1 + Percentage Change). Remember to express the percentage change as a decimal.
Q: Why are percentages useful?
A: Percentages provide a standardized way to compare proportions and express relative changes. They are widely used in finance, statistics, and everyday life to make informed decisions and understand complex information.
Conclusion
So, we've definitively answered the question: 19 is 76% of 25. But more than just finding the solution to a specific problem, we've explored the broader significance of percentages in our daily lives. From navigating discounts at the store to understanding complex financial data, a solid grasp of percentages empowers us to make informed decisions and critically analyze the information we encounter.
Understanding percentages is more than just a mathematical exercise; it's a life skill. By mastering the fundamentals, staying informed about current trends, and applying practical tips, you can unlock the power of percentages to navigate the world with greater confidence and clarity.
Now that you've deepened your understanding of percentages, put your knowledge to the test! Try applying these principles to real-world scenarios, explore online resources for further practice, and share your insights with others. Engage with the topic, ask questions, and continue to refine your skills. Your journey to mastering percentages has just begun, and the possibilities are endless.
Latest Posts
Latest Posts
-
Little Red Riding Hood Book Summary
Nov 22, 2025
-
How Old Is Paris From Romeo And Juliet
Nov 22, 2025
-
Summary Of The Story The Monkeys Paw
Nov 22, 2025
-
What Are A Group Of Peacocks Called
Nov 22, 2025
-
19 Is What Percent Of 25
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about 19 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.