20 Is 25 Percent Of What
sandbardeewhy
Nov 24, 2025 · 13 min read
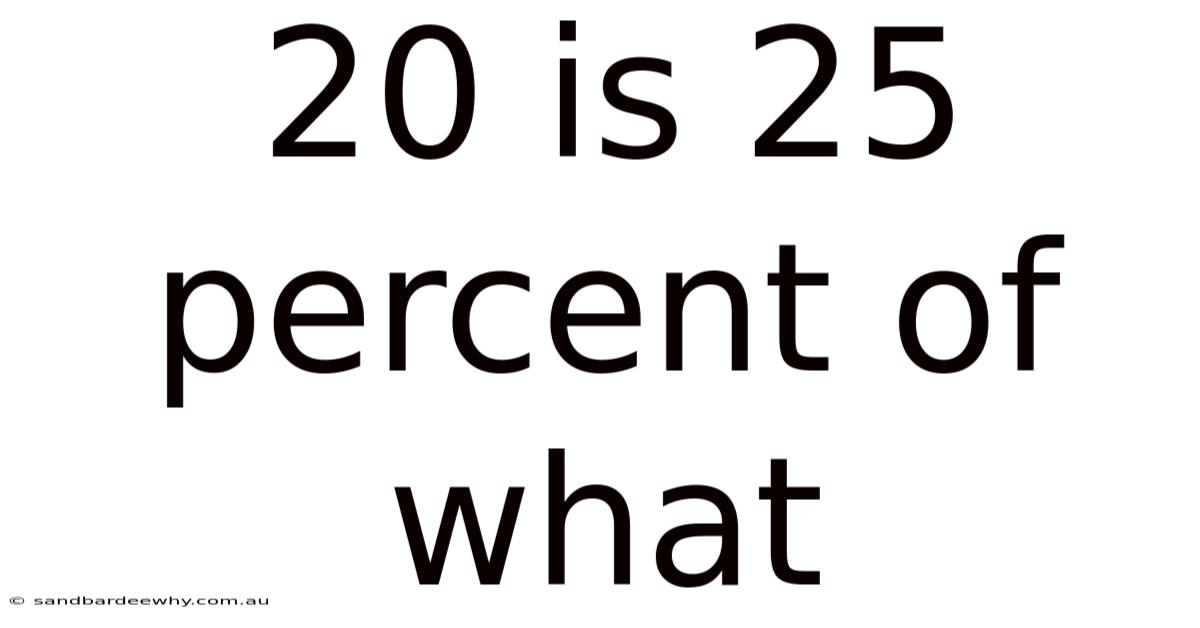
Table of Contents
Imagine you're at a bustling farmers market, eyeing a basket of ripe, juicy strawberries. A sign boasts "25% Off!" and the new price is $20. You're curious, how much were these beauties before the sale? Or perhaps you're splitting a restaurant bill with friends, and you decide to leave a generous 25% tip, which turns out to be $20. What was the original cost of the meal? These everyday scenarios require us to understand percentages and their relationship to whole numbers.
The ability to quickly and accurately calculate percentages is a valuable life skill. Whether you're figuring out discounts, calculating interest rates, or analyzing statistics, percentages are ubiquitous. One common type of percentage problem involves determining the original whole number when you know a percentage and its corresponding value. The question "20 is 25 percent of what?" falls squarely into this category. Understanding how to solve this type of problem can unlock a wide range of practical applications, empowering you to make informed decisions in various aspects of your life. So, let's delve into the world of percentages and learn how to crack this code!
Unveiling the Mystery: "20 is 25 Percent of What?"
At its core, the question "20 is 25 percent of what?" is asking us to find the original number (the whole) to which the percentage (25%) was applied, resulting in the value of 20. Understanding the underlying concepts is crucial before diving into specific methods of solving this type of problem. Let's break down the key elements:
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, 25 percent (25%) is equivalent to 25/100 or 0.25. Percentages are a standardized way to represent proportions and ratios, making it easier to compare different quantities. For example, saying that one candidate received 60% of the votes immediately gives you a sense of their level of support, regardless of the total number of votes cast.
The Relationship Between Percentages, Parts, and Wholes
The fundamental relationship we need to understand is this: Percentage x Whole = Part.
- The whole is the original or total quantity.
- The percentage is the fraction of the whole we are considering.
- The part is the value we get when we apply the percentage to the whole.
In the question "20 is 25 percent of what?", we know the part (20) and the percentage (25%), and we need to find the whole. This is a classic "missing whole" percentage problem. Visualizing this relationship can be helpful. Imagine a pie cut into slices. The whole pie represents 100%. A percentage represents a certain number of slices. We know the size of some slices (20), and we know the percentage of slices these represent (25%), and we need to find the size of the whole pie.
Setting Up the Problem
To solve this problem effectively, we need to translate the words into a mathematical equation. "20 is 25 percent of what?" can be rewritten as:
20 = 25% * x
Where 'x' represents the unknown whole number that we're trying to find. This equation forms the foundation for all the solution methods we will explore. The key is to isolate 'x' on one side of the equation to determine its value.
Common Misconceptions
One common mistake is confusing the part and the whole. It's crucial to identify what the percentage is being applied to. In this case, 25% is being applied to the unknown number ('x'), not to the number 20. Another misconception is forgetting to convert the percentage into a decimal or fraction before performing calculations. Failing to do so will lead to incorrect results.
Why This Matters
Understanding how to solve these types of percentage problems goes beyond simple math exercises. It's a practical skill that empowers you to navigate everyday financial and analytical situations with confidence. From calculating discounts and sales tax to understanding financial reports and statistics, the ability to work with percentages is invaluable. It also lays the groundwork for more advanced mathematical concepts, such as ratios, proportions, and statistical analysis.
Methods for Solving "20 is 25 Percent of What?"
There are several ways to solve the problem "20 is 25 percent of what?". Each method offers a slightly different approach, allowing you to choose the one that resonates best with your understanding and preferences. Let's explore some of the most common and effective methods:
1. The Equation Method
This method is based on directly translating the problem into a mathematical equation and solving for the unknown variable. As we established earlier, "20 is 25 percent of what?" translates to:
20 = 25% * x
To solve for 'x', we need to isolate it on one side of the equation. First, convert the percentage into a decimal by dividing by 100:
25% = 25/100 = 0.25
Now, substitute this value back into the equation:
20 = 0.25 * x
To isolate 'x', divide both sides of the equation by 0.25:
20 / 0.25 = x
x = 80
Therefore, 20 is 25 percent of 80.
2. The Proportion Method
The proportion method relies on the concept of equivalent ratios. We can set up a proportion that relates the part (20) to the percentage (25%) and the unknown whole (x) to 100%:
20 / x = 25 / 100
To solve this proportion, we can use cross-multiplication:
20 * 100 = 25 * x
2000 = 25x
Now, divide both sides by 25 to isolate 'x':
2000 / 25 = x
x = 80
Again, we find that 20 is 25 percent of 80.
3. The Fraction Method
This method involves converting the percentage into a fraction and then using that fraction to find the whole. We know that 25% is equal to 25/100, which can be simplified to 1/4. The problem then becomes:
20 is 1/4 of what?
If 20 represents one-quarter of the unknown number, then the whole number must be four times 20. Therefore:
x = 20 * 4
x = 80
This method highlights the direct relationship between fractions and percentages.
4. The "Thinking it Through" Method
Sometimes, a more intuitive approach can be just as effective. If 20 is 25% of a number, and 25% represents one-quarter, then we can deduce that the whole number is four times larger than 20. This method relies on mental math and a strong understanding of percentage equivalents.
25% is equivalent to 1/4.
If 20 = 1/4 of the number, then the whole number is 20 * 4 = 80.
This method is often faster for simpler percentage problems but may become more challenging with complex percentages.
Choosing the Right Method
The best method for solving "20 is 25 percent of what?" depends on your individual preferences and the specific context of the problem. The equation method is generally the most versatile and reliable, especially for more complex problems. The proportion method is useful for visualizing the relationship between percentages and wholes. The fraction method can be particularly efficient when dealing with common percentage equivalents like 25%, 50%, and 75%. And the "thinking it through" method is great for quick mental calculations. The key is to practice each method and become comfortable with the one that works best for you.
Trends and Real-World Applications
Understanding how to solve "20 is 25 percent of what?" has numerous practical applications in today's world. Let's examine some current trends and real-world scenarios where this skill is essential:
Retail and Discounts
One of the most common applications is in retail. When you see a sale offering a certain percentage off, you might want to calculate the original price of an item. For example, if a shirt is on sale for $20 after a 25% discount, you can use the methods described above to determine the original price. This helps you understand the true value of the discount and make informed purchasing decisions.
Finance and Investments
In finance, this type of calculation is crucial for understanding investment returns. If an investment generates a $20 profit, representing a 25% return on the initial investment, you can calculate the original investment amount. This knowledge is vital for assessing the performance of your investments and making strategic financial decisions.
Data Analysis and Statistics
Data analysts often use percentages to interpret data and draw conclusions. If a survey shows that 20 out of a group of people represent 25% of the total surveyed population, you can calculate the total number of people surveyed. This is essential for understanding the scope and representativeness of the data.
Real Estate
In real estate, understanding percentages is key for calculating commissions. If a real estate agent earns a $20 commission representing 25% of their total earnings on a sale, you can calculate their total earnings from that sale. This helps in understanding income and financial planning.
Academic Research
Researchers across various fields use percentages to analyze data and present findings. For instance, if a study finds that 20 students represent 25% of the class that achieved a certain milestone, one can calculate the total number of students in the class. This is useful in academic evaluations and assessments.
Budgeting and Personal Finance
In personal finance, you can use this skill to manage your budget effectively. For instance, if you allocate $20 for entertainment which represents 25% of your discretionary spending, you can calculate your total discretionary spending. This helps in tracking and optimizing your financial habits.
Professional Insight
From a professional standpoint, the ability to quickly and accurately calculate percentages is highly valued. Employers across various industries look for candidates with strong quantitative skills, including the ability to work with percentages. This skill demonstrates analytical thinking and problem-solving abilities, which are crucial for success in many roles. Moreover, the increasing reliance on data-driven decision-making in businesses makes percentage calculations even more vital. Understanding how to extract meaningful insights from data using percentages can give you a competitive edge in the job market.
Expert Tips and Practical Advice
Mastering the art of percentage calculations, particularly solving "20 is 25 percent of what?", involves more than just memorizing formulas. Here are some expert tips and practical advice to enhance your skills and ensure accuracy:
1. Practice Regularly
Like any skill, proficiency in percentage calculations requires consistent practice. Dedicate time each day to solve different types of percentage problems. Use online resources, textbooks, or create your own scenarios to challenge yourself. The more you practice, the faster and more accurate you'll become.
2. Understand the Context
Before diving into calculations, take a moment to understand the context of the problem. Identify what the "part" represents, what the "percentage" signifies, and what the "whole" is supposed to be. Misinterpreting the context can lead to incorrect solutions. Ask yourself: What is being compared to what? What is the base value?
3. Use Estimation
Develop your estimation skills to check the reasonableness of your answers. Before calculating the exact answer, estimate the approximate value. For instance, if 20 is 25% of a number, you know that the number must be larger than 20. Since 25% is one-quarter, the number should be around four times 20, which is 80. This estimation can help you identify obvious errors in your calculations.
4. Break Down Complex Problems
When faced with complex percentage problems, break them down into smaller, more manageable steps. Identify the individual components and solve them one at a time. For example, if you need to calculate multiple discounts or taxes, handle each one separately to avoid confusion.
5. Leverage Technology
Take advantage of technology to simplify your calculations. Use calculators, spreadsheets, or online percentage calculators to perform calculations quickly and accurately. However, don't rely solely on technology. Make sure you understand the underlying concepts and can perform the calculations manually as well. Technology should be a tool to enhance your skills, not replace them.
6. Master Percentage Equivalents
Familiarize yourself with common percentage equivalents, such as 25% = 1/4, 50% = 1/2, 75% = 3/4, and 10% = 1/10. Knowing these equivalents can significantly speed up your calculations and make mental math easier. Create a cheat sheet or flashcards to memorize these values.
7. Use Visual Aids
Visual aids can be helpful for understanding and solving percentage problems. Draw diagrams, charts, or graphs to represent the relationships between percentages, parts, and wholes. Visualizing the problem can make it easier to grasp and solve.
8. Double-Check Your Work
Always double-check your work to ensure accuracy. Review your calculations, and verify that your answer makes sense in the context of the problem. If possible, use a different method to solve the problem and compare the results.
9. Seek Feedback
Don't hesitate to seek feedback from others. Ask friends, family members, or colleagues to review your work and provide suggestions for improvement. Consider joining a math study group or seeking help from a tutor.
10. Apply in Real-Life Situations
Look for opportunities to apply your percentage calculation skills in real-life situations. Calculate discounts while shopping, estimate tips at restaurants, or analyze financial reports. The more you apply your skills, the more confident and proficient you'll become.
Frequently Asked Questions (FAQ)
Q: What does "percent" mean?
A: "Percent" means "out of one hundred." It's a way of expressing a number as a fraction of 100.
Q: How do I convert a percentage to a decimal?
A: Divide the percentage by 100. For example, 25% = 25/100 = 0.25.
Q: How do I convert a decimal to a percentage?
A: Multiply the decimal by 100. For example, 0.50 = 0.50 * 100 = 50%.
Q: What is the formula for calculating a percentage?
A: Percentage = (Part / Whole) * 100
Q: How do I find the whole if I know the part and the percentage?
A: Divide the part by the decimal equivalent of the percentage. For example, if 20 is 25% of a number, then the number is 20 / 0.25 = 80.
Q: Can percentages be greater than 100%?
A: Yes, percentages can be greater than 100%. This typically occurs when there is an increase or growth exceeding the original value. For example, if a company's revenue increases by 150%, it means the revenue is now 2.5 times the original revenue.
Q: Is there a difference between percentage increase and percentage decrease?
A: Yes, percentage increase and percentage decrease represent changes in opposite directions. Percentage increase calculates how much a value has increased relative to its original value, while percentage decrease calculates how much a value has decreased relative to its original value. The formulas are slightly different:
- Percentage Increase = [(New Value - Original Value) / Original Value] * 100
- Percentage Decrease = [(Original Value - New Value) / Original Value] * 100
Conclusion
The question "20 is 25 percent of what?" might seem simple, but mastering its solution unveils a deeper understanding of percentages and their applications. Whether you prefer the equation method, the proportion method, the fraction method, or a more intuitive approach, the key is to grasp the underlying relationship between percentages, parts, and wholes. Regular practice, a solid understanding of context, and the application of expert tips can transform you into a percentage-solving pro.
From calculating discounts and analyzing financial data to interpreting statistics and managing personal finances, the ability to work with percentages is an invaluable skill in today's world. So, embrace the challenge, hone your skills, and unlock the power of percentages to make informed decisions and achieve your goals.
Now that you've mastered this concept, why not test your skills further? Try solving similar percentage problems with different numbers and scenarios. Share your solutions and insights in the comments below, and let's continue learning and growing together!
Latest Posts
Latest Posts
-
Summary Lord Of The Flies Chapter 10
Nov 24, 2025
-
Numbers Of Jehovahs Witnesses Year 1925
Nov 24, 2025
-
Write The Following Equation In Its Equivalent Logarithmic Form
Nov 24, 2025
-
What Biome Has The Most Diverse Plant And Animal Life
Nov 24, 2025
-
20 Is 25 Percent Of What
Nov 24, 2025
Related Post
Thank you for visiting our website which covers about 20 Is 25 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.