20 Is What Percent Of 80
sandbardeewhy
Nov 21, 2025 · 11 min read
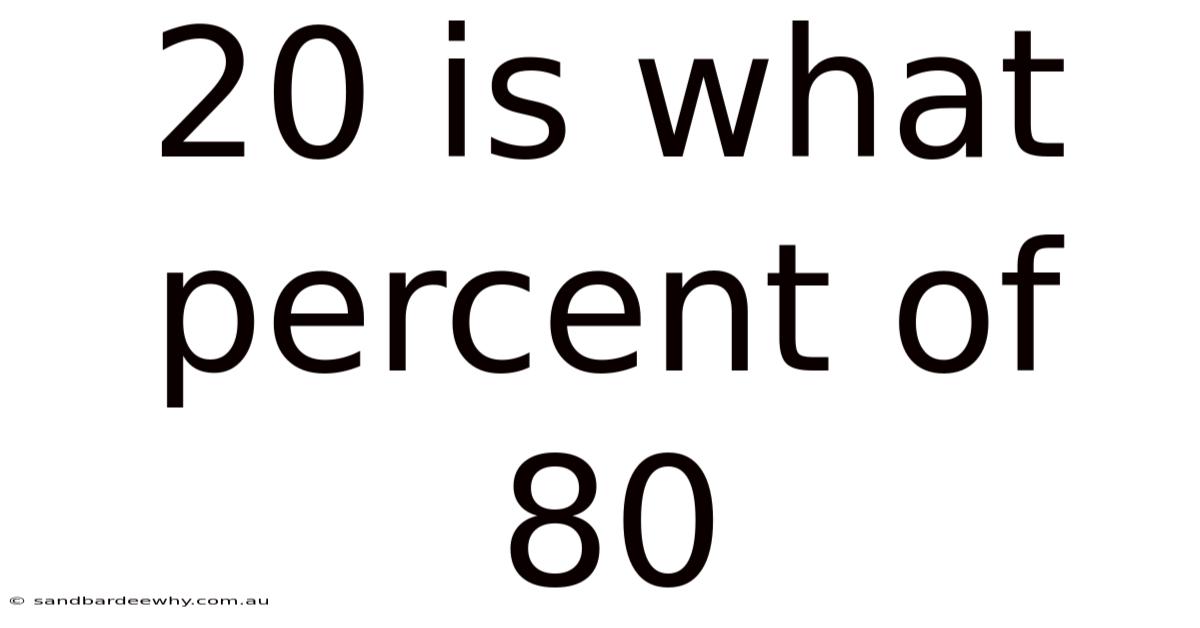
Table of Contents
The aroma of freshly brewed coffee filled the air as Sarah prepared for her morning math tutoring session. Her student, a bright-eyed teenager named Emily, was struggling with percentage problems. Sarah remembered her own struggles with math in high school and made a mental note to break down each concept as simply as possible. Today’s challenge was a classic: "20 is what percent of 80?" A seemingly straightforward question, yet one that often tripped students up.
Sarah smiled reassuringly at Emily. "Okay, let's tackle this problem together," she said. "Remember, percentages are just a way of expressing a fraction out of 100. So, when we ask, '20 is what percent of 80?', we're essentially asking, 'What fraction of 80 is 20, and how would we represent that fraction as a percentage?'" With a deep breath, Emily nodded, ready to embark on another mathematical adventure.
Unveiling the Mystery: 20 is What Percent of 80?
Understanding percentages is a fundamental skill with broad applications in everyday life. From calculating discounts at the store to understanding interest rates on loans, percentages help us make informed decisions. However, many people find percentage problems confusing. One such common problem is determining what percentage a smaller number represents of a larger one, such as calculating "20 is what percent of 80." This article aims to provide a comprehensive guide to solving this type of percentage problem, explaining the underlying concepts, and offering practical tips and real-world examples.
This mathematical challenge, "20 is what percent of 80", is more than just a textbook exercise; it represents a basic yet crucial aspect of proportional reasoning. At its core, the problem requires us to understand the relationship between two quantities and express that relationship as a percentage. Percentages, derived from the Latin per centum meaning "out of one hundred," provide a standardized way to compare fractions and ratios. This makes them incredibly useful in various contexts, from finance and economics to everyday shopping and cooking. By mastering the method to calculate percentages, individuals gain a valuable tool for analyzing data, making informed decisions, and understanding the world around them.
Comprehensive Overview
The concept of percentages has a rich history and is deeply rooted in mathematical principles. To fully grasp how to solve "20 is what percent of 80," it's helpful to understand the definitions, history, and mathematical foundations involved.
Definitions and Basic Concepts
A percentage is a way of expressing a number as a fraction of 100. It is denoted by the percent sign "%." For example, 50% means 50 out of 100, or 50/100.
The basic formula for calculating a percentage is: Percentage = (Part / Whole) × 100
In the problem "20 is what percent of 80," 20 is the part, and 80 is the whole. We are trying to find what percentage the part (20) represents of the whole (80).
Historical Roots of Percentages
The use of percentages dates back to ancient Rome. As the Roman Empire expanded, taxes were often calculated as fractions of goods sold or traded. The Romans used various fractions, including fractions of 100, to simplify these calculations. However, the modern concept of percentages as we know it today developed during the Renaissance.
During the 15th century, as trade and commerce flourished, there was an increasing need for a standardized way to calculate interest, profit margins, and taxes. Italian merchants began using percentages regularly. The first known explicit use of the percent sign (%) can be traced back to manuscripts from this period.
Mathematical Foundations
The mathematical foundation of percentages lies in the concept of ratios and proportions. A ratio is a comparison of two quantities, while a proportion is an equality between two ratios. Percentages are essentially a special type of ratio where the denominator is always 100.
To solve "20 is what percent of 80," we set up a proportion:
20 / 80 = x / 100
Here, x represents the percentage we are trying to find. By cross-multiplying and solving for x, we can determine the percentage.
Step-by-Step Calculation
To calculate "20 is what percent of 80," follow these steps:
- Identify the Part and the Whole: In this case, 20 is the part, and 80 is the whole.
- Formulate the Fraction: Create a fraction with the part as the numerator and the whole as the denominator: 20 / 80.
- Simplify the Fraction: Simplify the fraction to its simplest form. 20 / 80 simplifies to 1 / 4.
- Convert to Decimal: Convert the simplified fraction to a decimal by dividing the numerator by the denominator: 1 ÷ 4 = 0.25.
- Convert to Percentage: Multiply the decimal by 100 to convert it to a percentage: 0.25 × 100 = 25%.
Therefore, 20 is 25% of 80.
Alternative Methods
Another way to approach this problem is by using the direct percentage formula:
Percentage = (Part / Whole) × 100 Percentage = (20 / 80) × 100 Percentage = 0.25 × 100 Percentage = 25%
This method bypasses the simplification step and directly calculates the percentage.
Trends and Latest Developments
While the basic principles of calculating percentages remain unchanged, their application and interpretation are constantly evolving due to technological advancements and data analysis trends.
Data Visualization and Percentages
In today's data-driven world, percentages are often used in data visualization tools and dashboards to present information in an understandable format. Software like Tableau, Power BI, and Google Data Studio allow users to create interactive charts and graphs that display percentages, making it easier to identify trends and patterns.
For example, a marketing team might use percentages to track the conversion rate of a website. By visualizing this data, they can quickly see what percentage of visitors are completing a desired action, such as making a purchase or filling out a form.
Machine Learning and Statistical Analysis
Machine learning algorithms and statistical analysis techniques often rely on percentages to evaluate model performance and interpret results. For instance, in classification tasks, accuracy is commonly expressed as a percentage to indicate the proportion of correctly classified instances.
Furthermore, percentages are used in hypothesis testing to determine the statistical significance of findings. P-values, which represent the probability of obtaining results as extreme as, or more extreme than, the observed results, are often interpreted in the context of percentages to assess the reliability of research conclusions.
E-commerce and Retail Analytics
E-commerce platforms heavily rely on percentages to optimize sales and improve customer experience. Conversion rates, click-through rates, and churn rates are all key metrics that are expressed as percentages. By analyzing these metrics, retailers can identify areas for improvement and make data-driven decisions.
For example, an e-commerce site might track the percentage of users who add items to their cart but do not complete the purchase (cart abandonment rate). By understanding this percentage, they can implement strategies to reduce cart abandonment, such as offering free shipping or sending reminder emails.
Expert Insights
According to financial analysts, understanding percentage changes is critical for assessing investment performance. A small percentage increase in a portfolio can translate to significant gains over time, while a percentage decrease can indicate potential risks. Experts recommend that investors pay close attention to percentage returns, inflation rates, and interest rates when making financial decisions.
Additionally, educators emphasize the importance of teaching percentage concepts in a practical and engaging manner. By relating percentages to real-world scenarios, such as calculating discounts or understanding statistics in sports, students are more likely to grasp the underlying principles and retain the knowledge.
Tips and Expert Advice
To master percentage calculations and avoid common pitfalls, consider the following tips and expert advice:
Practice Regularly
Like any mathematical skill, proficiency in percentage calculations requires practice. Work through a variety of problems to reinforce your understanding and build confidence. Start with simple problems and gradually increase the complexity. Use online resources, textbooks, or worksheets to find practice exercises.
For example, challenge yourself with questions like "30 is what percent of 120?" or "75 is what percent of 200?" The more you practice, the more comfortable you will become with the process.
Understand the Context
Always pay attention to the context of the problem. Misunderstanding the context can lead to incorrect calculations. Identify what is the part and what is the whole in the given scenario. Be clear about what you are trying to find.
For instance, if a store offers a 20% discount on an item priced at $80, it is crucial to understand that the discount is a percentage of the original price. The discount amount is 20% of $80, which is $16. The final price is then $80 - $16 = $64.
Use Real-World Examples
Relate percentage calculations to real-world examples to make the concept more tangible. Use scenarios from your daily life, such as calculating tips at a restaurant, figuring out sales tax, or determining the percentage of calories from fat in a food item.
By connecting percentages to practical situations, you will not only improve your understanding but also appreciate the relevance of this mathematical concept.
Double-Check Your Work
Always double-check your work to ensure accuracy. A small error in calculation can lead to a significant difference in the final result. Use estimation techniques to verify whether your answer is reasonable.
For example, if you calculate that 20 is 40% of 80, you should realize that this is incorrect because 40% of 80 would be 32, not 20. This simple check can help you catch mistakes and correct them.
Use Online Calculators and Tools
Take advantage of online percentage calculators and tools to verify your answers and explore different scenarios. These tools can save time and provide immediate feedback, allowing you to learn from your mistakes.
However, do not rely solely on these tools. It is essential to understand the underlying principles and be able to perform the calculations manually. Use calculators as a supplement to your learning, not as a replacement for it.
Seek Help When Needed
Do not hesitate to seek help from teachers, tutors, or online resources if you are struggling with percentage calculations. Asking for assistance is a sign of strength, not weakness. A clear explanation from someone who understands the concept can make a significant difference.
Many online forums and communities are dedicated to math help. These platforms can provide valuable insights and support from fellow learners and experts.
FAQ
Q: What is a percentage? A: A percentage is a way of expressing a number as a fraction of 100. It is denoted by the percent sign (%).
Q: How do I calculate what percentage one number is of another? A: Use the formula: Percentage = (Part / Whole) × 100.
Q: Can a percentage be greater than 100%? A: Yes, a percentage can be greater than 100%. This usually indicates an increase or a ratio greater than 1:1. For example, if a quantity doubles, it represents a 100% increase, resulting in a final value that is 200% of the original.
Q: What are some common mistakes to avoid when calculating percentages? A: Common mistakes include misidentifying the part and the whole, not simplifying fractions correctly, and making errors in decimal conversion.
Q: How are percentages used in real life? A: Percentages are used in various real-life scenarios, such as calculating discounts, determining interest rates, understanding statistics, and analyzing data.
Q: Is there a quick way to estimate percentages? A: Yes, you can estimate percentages by rounding numbers to the nearest 10 or 25 and using mental math techniques. For example, 25% is equivalent to one-quarter, and 10% is equivalent to one-tenth.
Conclusion
Understanding how to calculate "20 is what percent of 80" is a foundational skill that empowers you to make sense of the world around you. By grasping the basic concepts, historical context, and mathematical foundations, you can confidently tackle percentage problems in various situations. Remember, the key is to identify the part and the whole, formulate the fraction, and convert it to a percentage using the formula: Percentage = (Part / Whole) × 100.
As you continue to explore the world of mathematics, remember that practice and perseverance are essential. Embrace the challenges, seek help when needed, and celebrate your successes along the way. Now that you've mastered this concept, why not try applying your newfound knowledge to real-world scenarios? Calculate the discount on your next purchase, analyze the statistics in your favorite sport, or explore the world of finance with a better understanding of interest rates and investment returns. Share your insights and experiences in the comments below, and let's continue to learn and grow together.
Latest Posts
Latest Posts
-
How Much Is 100 Gallons Of Water
Nov 21, 2025
-
What Element Has 5 Valence Electrons
Nov 21, 2025
-
How Many Ounces In A Gallon
Nov 21, 2025
-
20 Is What Percent Of 80
Nov 21, 2025
-
Forms Of To Be In German
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.