32 Is 40 Of What Number
sandbardeewhy
Nov 27, 2025 · 12 min read
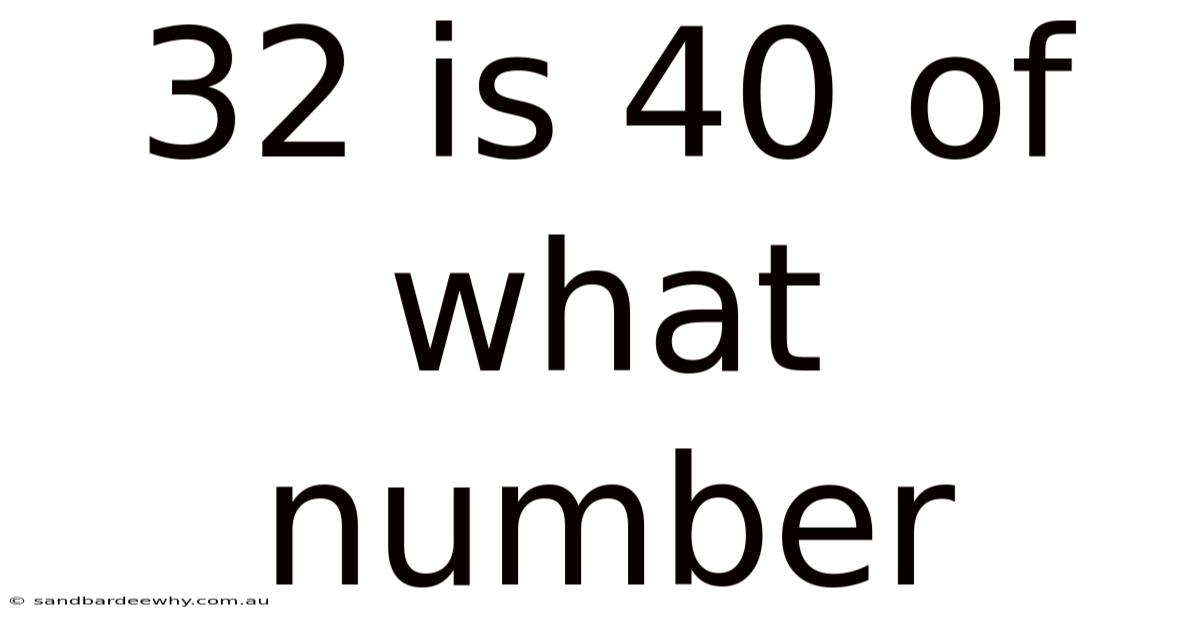
Table of Contents
Imagine you're at a bustling farmer's market, carefully selecting the freshest produce. You spot a sign: "Today, get 32 apples for 40% off!" Intrigued, you wonder, "What was the original price of these apples before the discount?" This everyday scenario highlights the importance of understanding percentage problems and how to solve for the original whole. Questions like "32 is 40% of what number?" are not just mathematical exercises; they're practical skills that empower us to make informed decisions in various aspects of life.
At its core, solving "32 is 40% of what number?" involves deciphering the relationship between a part (32), a percentage (40%), and the whole (the unknown number). This type of problem falls under the umbrella of percentage calculations, a fundamental concept in mathematics with broad applications. Whether you're calculating discounts, analyzing financial data, or interpreting statistical reports, the ability to confidently tackle percentage problems is invaluable. This article will delve into the mechanics of solving this specific question, explore the underlying principles of percentage calculations, and provide practical tips and real-world examples to solidify your understanding.
Main Subheading
Percentage problems have been a staple of mathematical education and practical applications for centuries. Understanding their historical context and conceptual foundations helps appreciate their ongoing relevance.
Percentages, derived from the Latin per centum meaning "out of one hundred," emerged as a standardized way to express proportions and ratios. Historically, various cultures used different fractions and proportions for calculations, leading to inconsistencies and complexities. The adoption of percentages provided a uniform system that simplified comparisons and facilitated trade and financial transactions.
The conceptual foundation of percentages rests on the idea of representing a part of a whole as a fraction with a denominator of 100. This normalization allows for easy comparison of different proportions, regardless of the size of the original whole. For instance, saying that 40% of a group supports a particular policy provides a clear understanding of the level of support, even without knowing the exact size of the group.
The question "32 is 40% of what number?" is a classic example of an inverse percentage problem. Instead of finding a percentage of a given number, we are given a percentage and its corresponding value and asked to find the original whole. This requires a slightly different approach than typical percentage calculations, often involving algebraic manipulation or the use of proportions.
Comprehensive Overview
To truly understand how to solve "32 is 40% of what number?", it's essential to break down the problem into its core components and explore different solution methods. This section will cover definitions, mathematical approaches, and alternative perspectives to deepen your understanding.
Defining the Components:
- Percentage: A percentage is a way of expressing a number as a fraction of 100. It is denoted by the symbol "%". In this problem, the percentage is 40%.
- Part: The part is the value that represents a certain percentage of the whole. In this problem, the part is 32.
- Whole: The whole is the original or total number that we are trying to find. In this problem, the whole is the unknown number.
Mathematical Approaches:
There are several ways to solve this problem mathematically. Here are three common methods:
-
Using a Proportion:
- Set up a proportion: part / whole = percentage / 100
- Plug in the known values: 32 / x = 40 / 100
- Cross-multiply: 32 * 100 = 40 * x
- Simplify: 3200 = 40x
- Solve for x: x = 3200 / 40
- x = 80
-
Using an Equation:
- Translate the problem into an equation: 32 = 0.40 * x
- Solve for x: x = 32 / 0.40
- x = 80
-
Using the Formula:
- The formula for finding the whole is: Whole = Part / (Percentage / 100)
- Plug in the values: Whole = 32 / (40 / 100)
- Whole = 32 / 0.40
- Whole = 80
Scientific Foundations:
The underlying scientific principle behind percentage calculations is the concept of proportionality. Proportionality describes the relationship between two quantities that vary directly with each other. In the context of percentages, the part is directly proportional to the whole, with the percentage acting as the constant of proportionality.
This concept is widely used in various scientific disciplines, including:
- Statistics: Percentages are used to express probabilities, confidence intervals, and other statistical measures.
- Chemistry: Percentages are used to express the concentration of solutions and the composition of mixtures.
- Physics: Percentages are used to express errors in measurements and the efficiency of machines.
Understanding the Conceptually:
Imagine a pie chart representing the whole (the unknown number). This pie chart is divided into 100 equal slices, each representing 1%. We know that 40 of these slices (40%) represent the value of 32. To find the value of the entire pie chart (the whole), we need to determine the value of one slice and then multiply it by 100.
Since 40 slices represent 32, one slice represents 32 / 40 = 0.8. Therefore, the entire pie chart (100 slices) represents 0.8 * 100 = 80.
This conceptual understanding can be helpful for visualizing percentage problems and developing a deeper intuition for their solutions.
Alternative Perspectives:
Another way to think about this problem is to consider the ratio of the part to the percentage. In this case, the ratio is 32 / 40 = 0.8. This ratio represents the value of 1% of the whole. To find the whole, we simply multiply this ratio by 100: 0.8 * 100 = 80.
This approach emphasizes the relationship between the part, the percentage, and the whole, and can be useful for solving more complex percentage problems.
Trends and Latest Developments
While the fundamental principles of percentage calculations remain constant, their application and relevance evolve with changing trends and technological advancements.
Data Analysis and Visualization:
In today's data-driven world, percentages are ubiquitous in data analysis and visualization. They are used to summarize and present data in a clear and concise manner, making it easier to identify trends, patterns, and insights. Tools like spreadsheets, statistical software, and data visualization platforms rely heavily on percentage calculations to generate reports, charts, and dashboards.
E-commerce and Online Marketing:
Percentages play a crucial role in e-commerce and online marketing. Discounts, sales tax, conversion rates, and click-through rates are all expressed as percentages. Understanding how to calculate and interpret these percentages is essential for businesses to optimize their marketing campaigns, pricing strategies, and overall profitability.
Financial Analysis and Investment:
Percentages are fundamental to financial analysis and investment. Interest rates, returns on investment, portfolio allocation, and risk assessment are all expressed as percentages. Investors use these percentages to evaluate investment opportunities, manage their portfolios, and make informed financial decisions.
Professional Insights:
From a professional standpoint, a strong understanding of percentage calculations is a basic requirement across various industries. Financial analysts, marketers, sales professionals, and even project managers need to be comfortable working with percentages to perform their jobs effectively.
- Staying Updated: Keep abreast of industry-specific applications of percentage calculations. For example, in marketing, understanding how algorithms calculate ad performance metrics requires continuous learning.
- Leveraging Technology: Utilize software and tools that automate percentage calculations and data analysis. This can save time and improve accuracy.
- Critical Thinking: Don't blindly accept percentage figures. Always question the underlying data and assumptions to ensure the accuracy and validity of the results.
Emerging Trends:
- AI-Powered Data Analysis: Artificial intelligence (AI) is increasingly being used to automate data analysis and identify patterns that might be missed by human analysts. This includes using AI to calculate and interpret percentages in complex datasets.
- Personalized Marketing: Percentages are being used to personalize marketing messages and offers to individual customers. By analyzing customer data, businesses can identify the products and services that are most likely to appeal to each customer and tailor their marketing accordingly.
- Financial Literacy: There is a growing emphasis on financial literacy, with a focus on teaching individuals how to understand and use percentages to make informed financial decisions.
Tips and Expert Advice
Mastering percentage problems requires not only understanding the underlying concepts but also developing practical skills and strategies. Here are some tips and expert advice to help you tackle these problems with confidence:
Tip 1: Understand the Language of Percentages
Percentages have their own vocabulary. Familiarize yourself with common terms like "percent increase," "percent decrease," "markup," "margin," and "discount." Understanding what these terms mean is crucial for interpreting percentage problems correctly.
For example, a "percent increase" indicates how much a value has increased relative to its original value, while a "percent decrease" indicates how much a value has decreased. A "markup" is the amount added to the cost of a product to determine its selling price, while a "margin" is the percentage of revenue that remains after deducting the cost of goods sold. Knowing these distinctions can prevent misinterpretations and errors.
Tip 2: Convert Percentages to Decimals or Fractions
When performing calculations with percentages, it's often easier to convert them to decimals or fractions. To convert a percentage to a decimal, divide it by 100. For example, 40% becomes 0.40. To convert a percentage to a fraction, write it as a fraction with a denominator of 100 and simplify if possible. For example, 40% becomes 40/100, which simplifies to 2/5.
Using decimals or fractions can simplify calculations and reduce the risk of errors. For example, instead of calculating 40% of 50, you can simply multiply 0.40 by 50 or multiply 2/5 by 50.
Tip 3: Use the "Is Over Of" Method
The "is over of" method is a helpful mnemonic for setting up proportions. The problem "32 is 40% of what number?" can be translated as "32 is over what number, as 40 is over 100." This leads to the proportion: 32 / x = 40 / 100.
This method provides a structured approach to setting up proportions, making it easier to identify the known and unknown values and solve for the unknown.
Tip 4: Estimate and Check Your Answers
Before performing any calculations, try to estimate the answer. This can help you identify potential errors and ensure that your final answer is reasonable. After you've calculated the answer, check it by plugging it back into the original problem.
For example, in the problem "32 is 40% of what number?", you might estimate that the answer is around 80. If your calculation yields an answer of 800, you know that you've made an error somewhere. Checking your answer by multiplying 80 by 0.40 confirms that it equals 32, indicating that your answer is correct.
Tip 5: Practice Regularly
Like any mathematical skill, mastering percentage problems requires regular practice. Work through a variety of problems, starting with simple ones and gradually progressing to more complex ones. Use online resources, textbooks, or worksheets to find practice problems.
The more you practice, the more comfortable you'll become with the different types of percentage problems and the various strategies for solving them. You'll also develop a better intuition for percentages, which will help you estimate answers and identify potential errors.
Expert Advice:
- Understand the Context: Pay attention to the context of the problem. What is being measured? What are the units? Understanding the context can help you interpret the problem correctly and choose the appropriate solution method.
- Break Down Complex Problems: If you're faced with a complex percentage problem, break it down into smaller, more manageable steps. Identify the key information and the relationships between the different values.
- Use Visual Aids: Visual aids like diagrams, charts, and graphs can be helpful for visualizing percentage problems and understanding the relationships between the different values.
- Seek Help When Needed: Don't be afraid to ask for help if you're struggling with percentage problems. Talk to a teacher, tutor, or classmate. There are also many online resources available to help you learn about percentages.
FAQ
Q: What is the difference between percent increase and percent decrease?
A: Percent increase measures how much a value has grown relative to its original value, while percent decrease measures how much a value has shrunk. The formulas are:
- Percent Increase = [(New Value - Original Value) / Original Value] * 100
- Percent Decrease = [(Original Value - New Value) / Original Value] * 100
Q: How do I calculate a percentage of a percentage?
A: To calculate a percentage of a percentage, convert both percentages to decimals and multiply them together. For example, to calculate 20% of 50%, multiply 0.20 by 0.50, which equals 0.10 or 10%.
Q: What is the difference between markup and margin?
A: Markup is the amount added to the cost of a product to determine its selling price, while margin is the percentage of revenue that remains after deducting the cost of goods sold. They are calculated differently:
- Markup = (Selling Price - Cost) / Cost
- Margin = (Revenue - Cost of Goods Sold) / Revenue
Q: How can I use percentages in everyday life?
A: Percentages are used in many aspects of everyday life, including:
- Calculating discounts and sales tax
- Tracking personal finances and investments
- Interpreting statistics and survey results
- Understanding nutrition labels and ingredient lists
Q: What are some common mistakes to avoid when working with percentages?
A: Some common mistakes include:
- Forgetting to convert percentages to decimals or fractions before performing calculations
- Misinterpreting the context of the problem
- Not estimating and checking your answers
- Confusing percent increase with percent decrease
Conclusion
In conclusion, understanding how to solve problems like "32 is 40% of what number?" is a valuable skill that extends far beyond the classroom. It's a fundamental tool for navigating everyday situations, making informed decisions, and succeeding in various professional fields.
By mastering the concepts, exploring different solution methods, and practicing regularly, you can develop a strong intuition for percentages and tackle these problems with confidence. Remember to understand the language of percentages, convert percentages to decimals or fractions, use the "is over of" method, estimate and check your answers, and seek help when needed.
Now that you have a solid understanding of percentage calculations, take the next step and apply your knowledge to real-world scenarios. Start by calculating discounts at the store, analyzing your personal finances, or interpreting statistics in the news. The more you practice, the more proficient you'll become. Share this article with your friends and colleagues and encourage them to enhance their understanding of percentages. Let's empower ourselves and others with the knowledge and skills needed to thrive in a data-driven world.
Latest Posts
Latest Posts
-
Which Of The Following Is Not A Continuous Variable
Nov 27, 2025
-
Who Is Captain Beatty In The Book Fahrenheit 451
Nov 27, 2025
-
How Many Yards Is 90 Inches
Nov 27, 2025
-
What Is 2 Percent Of 40
Nov 27, 2025
-
Which Sentence Best Describes A Regressive Tax
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about 32 Is 40 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.