6 Is 15 Percent Of What Amount
sandbardeewhy
Nov 26, 2025 · 10 min read
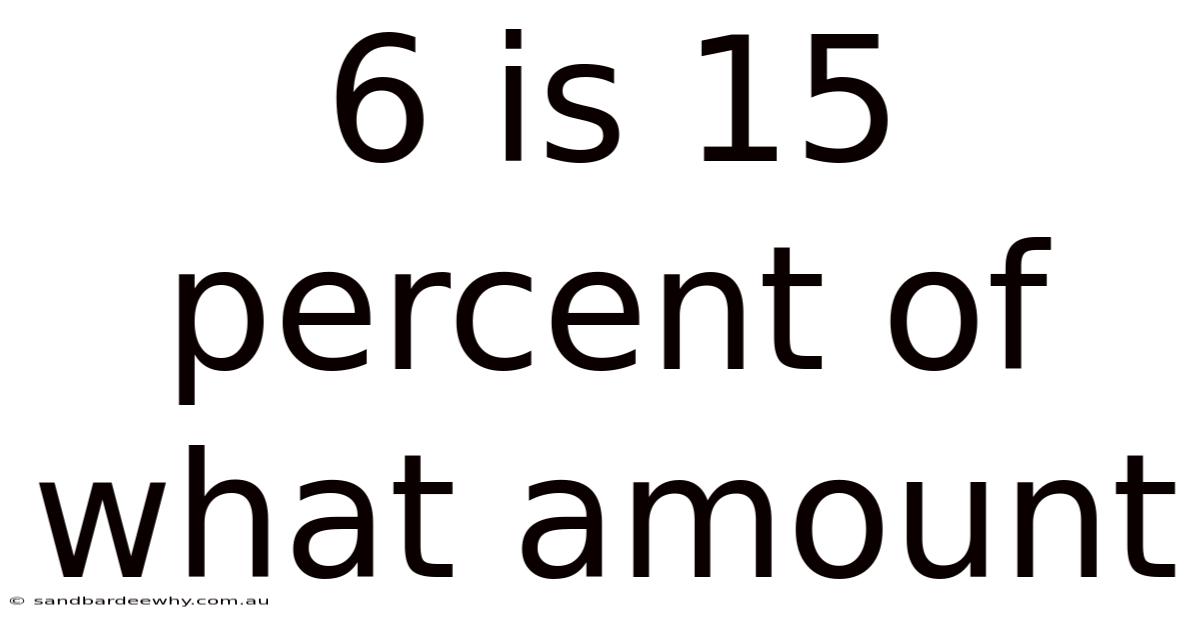
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a basket of ripe, juicy strawberries. The sign says "$6, and that's 15% off the original price!" Your mind races – how much were these beauties before the discount? Or picture yourself at a cozy bookstore, a captivating novel in hand. The cashier mentions, "This is part of our special promotion. The $6 you're paying is just 15% of the actual cost." Suddenly, you're not just a customer; you're a detective, trying to uncover the full story hidden behind those numbers.
The question "6 is 15 percent of what amount?" isn't just a mathematical puzzle; it's a real-life scenario that pops up in various contexts. Whether you're calculating discounts, understanding proportions, or simply trying to make sense of everyday transactions, mastering this type of percentage problem is incredibly useful. It equips you with the ability to analyze situations, make informed decisions, and confidently navigate the world of numbers that surrounds us.
Unveiling the Mystery: "6 is 15 Percent of What Amount?"
At its core, the question "6 is 15 percent of what amount?" is a percentage problem. To truly grasp what it entails, it's important to break down the components. The number "6" represents a portion or a part of an unknown whole. "15 percent" signifies the fraction (15/100 or 0.15) that this portion constitutes of that whole. The ultimate goal is to determine the value of that "whole" – the amount from which 6 is 15%. Understanding this relationship is the key to unlocking the solution.
Percentage problems like these are common in everyday life, from calculating tips at restaurants to figuring out interest rates on loans. They are also foundational in fields like finance, economics, and statistics. The ability to solve them accurately not only enhances your mathematical skills but also improves your overall financial literacy and decision-making capabilities. So, whether you're a student brushing up on math concepts or a professional seeking to sharpen your analytical tools, mastering the art of solving percentage problems is a valuable investment.
Comprehensive Overview: Diving Deep into Percentages
To solve "6 is 15 percent of what amount?", we need to fully understand what percentages are and how they work. Percentages are essentially fractions or ratios expressed as a portion of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." This "out of one hundred" concept is fundamental to understanding how percentages relate to whole numbers.
The concept of percentages has a rich history, dating back to ancient Rome. As the Roman Empire expanded, taxes and trade became increasingly complex. To simplify calculations, the Romans often used fractions based on 100, a precursor to modern percentages. For instance, Emperor Augustus levied a tax of 1/100 on goods sold at auction, known as centesima rerum venalium. This early use of hundredths helped standardize financial calculations across the empire.
During the Middle Ages, as trade flourished throughout Europe, the use of percentages became even more widespread. Italian merchants, known for their advanced mathematical skills, played a crucial role in popularizing percentages. They used them to calculate interest, profits, and losses in their business dealings. The symbols we use today for percentages (%) evolved gradually. In the 15th century, the Italian term "per cento" (for one hundred) was often abbreviated as "p cento" or "p. 100". Over time, this abbreviation morphed into the "%" symbol we recognize today.
The formal mathematical definition of a percentage involves expressing a part as a fraction of a whole, then multiplying by 100. Mathematically, if 'P' is the percentage, 'Part' is the portion, and 'Whole' is the total amount, then: P = (Part / Whole) * 100. Conversely, if you know the percentage and the part, you can find the whole using the formula: Whole = Part / (P/100). In our question, 6 is the 'Part' and 15% is 'P'.
Understanding this formula is crucial for solving percentage problems. To apply it, you need to correctly identify what each number represents in the context of the problem. The 'Part' is the specific amount you're interested in, the 'Whole' is the total amount, and the percentage expresses the relationship between the part and the whole. Recognizing these components allows you to set up the equation correctly and solve for the unknown variable, whether it's the percentage, the part, or the whole.
Trends and Latest Developments: Percentages in the Modern World
Percentages remain incredibly relevant in today's data-driven world. From financial analysis to market research, percentages are used to simplify complex information and make it easily understandable. In finance, interest rates, investment returns, and inflation rates are all expressed as percentages. This allows investors to compare different investment opportunities and assess their potential risks and rewards. In marketing, percentages are used to track market share, customer satisfaction, and the effectiveness of advertising campaigns.
One significant trend is the increasing use of data visualization tools that rely heavily on percentages. Charts, graphs, and dashboards often present data as percentages to highlight trends and patterns. This makes it easier for decision-makers to quickly grasp the key insights from large datasets. For example, a pie chart might show the percentage of revenue generated by different product lines, or a bar graph might display the percentage change in sales over time.
Another notable development is the growing emphasis on data literacy. With the proliferation of data in all aspects of life, it's becoming increasingly important to understand how to interpret and use percentages correctly. This includes being aware of potential biases and limitations in data, as well as understanding the statistical significance of percentage changes. For instance, a small percentage change in a large population may be more significant than a large percentage change in a small population.
Experts also emphasize the importance of understanding the context in which percentages are used. A percentage can be misleading if it's not presented in the right context. For example, a company might advertise a "50% off" sale, but if the original price was inflated, the final price might still be higher than the normal price at other stores. Similarly, a politician might claim that a certain policy reduced crime by 20%, but if overall crime rates were already declining, the impact of the policy might be overstated.
Furthermore, the rise of artificial intelligence (AI) and machine learning (ML) has led to new applications of percentages. AI algorithms often use percentages to express the probability of different outcomes or the confidence level of their predictions. For example, a spam filter might assign a 95% probability that an email is spam, or a medical diagnosis tool might give an 80% confidence level that a patient has a certain disease.
Tips and Expert Advice: Mastering the Art of Percentage Calculations
To effectively tackle percentage problems like "6 is 15 percent of what amount?", consider these expert tips and practical examples. First, always ensure you understand the question fully before attempting to solve it. Identify what is given (the part and the percentage) and what needs to be found (the whole). Misinterpreting the problem can lead to incorrect calculations and inaccurate results.
A crucial step is converting the percentage into a decimal or fraction. To convert a percentage to a decimal, divide it by 100. For example, 15% becomes 15/100 = 0.15. Alternatively, you can express the percentage as a fraction in its simplest form. 15% is equivalent to 15/100, which simplifies to 3/20. Using the decimal form is often more convenient for calculations, especially when using a calculator.
Now, let's apply this to our original question: "6 is 15 percent of what amount?". We know that 6 is the 'Part' and 15% (or 0.15) is the percentage. We need to find the 'Whole'. Using the formula Whole = Part / (P/100), we get: Whole = 6 / 0.15. Performing the division, we find that the Whole = 40. Therefore, 6 is 15 percent of 40.
Another helpful strategy is to use proportions. A proportion is an equation that states that two ratios are equal. In this case, we can set up the proportion as follows: 15/100 = 6/x, where 'x' is the unknown whole. To solve for 'x', cross-multiply: 15 * x = 6 * 100, which simplifies to 15x = 600. Dividing both sides by 15, we get x = 40. This method provides an alternative way to arrive at the same answer.
Experts also recommend practicing regularly with various types of percentage problems. Start with simple examples and gradually increase the complexity. This will help you build confidence and develop a strong understanding of the underlying concepts. For example, try solving problems involving discounts, markups, interest rates, and percentage changes. Each type of problem requires a slightly different approach, but the fundamental principles remain the same.
Furthermore, always check your answer to ensure it makes sense in the context of the problem. Ask yourself, "Is the whole I found larger than the part I started with?". In this case, 40 is indeed larger than 6, which is what we would expect since 6 is only 15% of the whole. If your answer seems unreasonable, double-check your calculations and make sure you have correctly identified the part, the whole, and the percentage.
FAQ: Answering Your Burning Questions About Percentages
Q: What is the difference between percentage increase and percentage decrease? A: Percentage increase refers to the proportional increase in a quantity over time, calculated as [(New Value - Original Value) / Original Value] * 100. Conversely, percentage decrease refers to the proportional decrease in a quantity over time, calculated as [(Original Value - New Value) / Original Value] * 100. Both are expressed as percentages, but they represent opposite changes.
Q: How do I calculate a percentage of a number? A: To find a percentage of a number, convert the percentage to a decimal or fraction and then multiply it by the number. For example, to find 20% of 50, convert 20% to 0.20 and multiply it by 50: 0.20 * 50 = 10. Therefore, 20% of 50 is 10.
Q: Can a percentage be greater than 100%? A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an original value and the new value is more than double the original. For example, if a company's revenue increased from $100,000 to $250,000, the percentage increase would be [(250,000 - 100,000) / 100,000] * 100 = 150%.
Q: How are percentages used in everyday life? A: Percentages are used extensively in everyday life, including calculating discounts, determining tips at restaurants, understanding interest rates on loans and credit cards, interpreting statistics in news reports, and tracking progress towards goals. They provide a convenient way to express proportions and compare different quantities.
Q: What is the best way to practice percentage calculations? A: The best way to practice percentage calculations is to work through a variety of problems, starting with simple examples and gradually increasing the complexity. Use real-world scenarios to make the practice more engaging and relevant. Online resources, textbooks, and worksheets can provide additional practice problems and solutions.
Conclusion
In summary, understanding how to solve the question "6 is 15 percent of what amount?" involves grasping the fundamental principles of percentages and their applications. By converting percentages to decimals or fractions, using the appropriate formulas, and practicing regularly, you can confidently tackle a wide range of percentage problems. Remember, the key is to accurately identify the part, the whole, and the percentage, and to double-check your answers to ensure they make sense in the context of the problem.
Now that you've unlocked the secrets of percentage calculations, put your skills to the test. Think about how you can apply this knowledge in your daily life, whether it's calculating discounts while shopping, understanding financial reports, or simply making informed decisions. Share this article with friends or colleagues who might benefit from learning about percentages, and encourage them to practice and improve their skills. By mastering the art of percentage calculations, you'll be well-equipped to navigate the world of numbers with confidence and accuracy.
Latest Posts
Latest Posts
-
Who Is The Narrator In The Outsiders
Nov 26, 2025
-
What Is The Input In Math
Nov 26, 2025
-
Definition Of Zero Pair In Math
Nov 26, 2025
-
6 Is 15 Percent Of What Amount
Nov 26, 2025
-
Native American Indian Symbol For Family
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about 6 Is 15 Percent Of What Amount . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.